Содержание
- 2. 1.1. Магнитные взаимодействия 1.2. Закон Био-Савара-Лапласа 1.3. Магнитное поле движущегося заряда 1.4. Напряженность магнитного поля 1.5.
- 3. В пространстве, окружающем намагниченные тела, возникает магнитное поле. Помещенная в это поле маленькая магнитная стрелка устанавливается
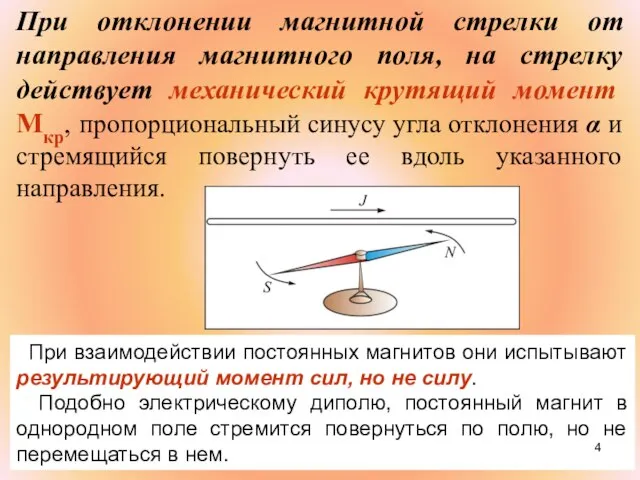
- 4. При отклонении магнитной стрелки от направления магнитного поля, на стрелку действует механический крутящий момент Мкр, пропорциональный
- 5. Отличие постоянных магнитов от электрических диполей заключается в следующем: Электрический диполь всегда состоит из зарядов, равных
- 6. Подводя итоги сведениям о магнетизме, накопленным к 1600 г., английский ученый-физик Уильям Гильберт написал труд «О
- 8. В своих трудах У. Гильберт высказал мнение, что, несмотря на некоторое внешнее сходство, природа электрических и
- 9. В 1820 г. Х. Эрстед открыл магнитное поле электрического тока. А. Ампер установил законы магнитного взаимодействия
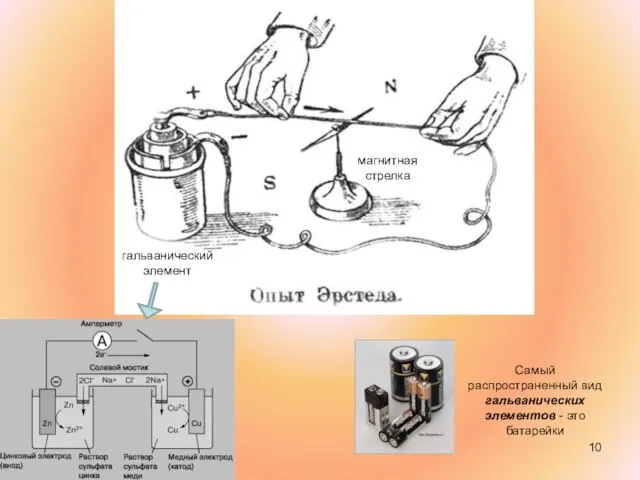
- 10. гальванический элемент магнитная стрелка Самый распространенный вид гальванических элементов - это батарейки
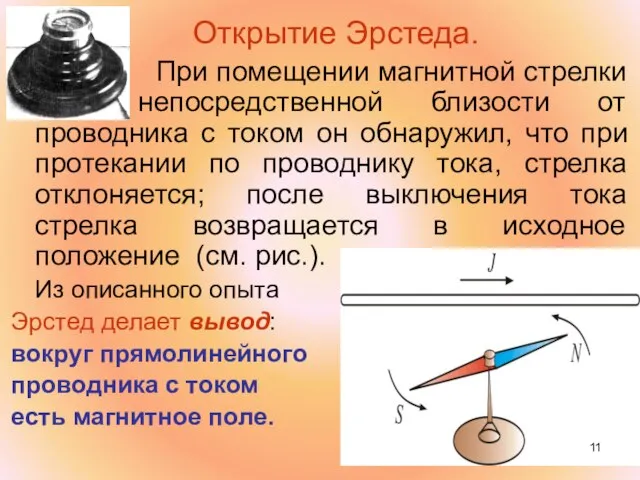
- 11. Открытие Эрстеда. При помещении магнитной стрелки в непосредственной близости от проводника с током он обнаружил, что
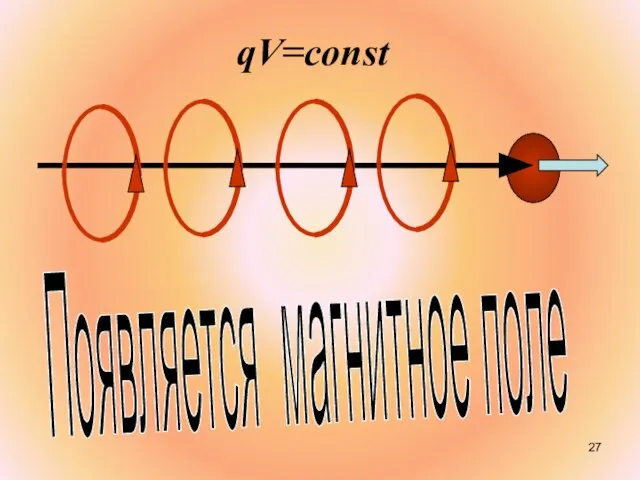
- 12. Общий вывод: вокруг всякого проводника с током есть магнитное поле. Но ведь ток – это направленное
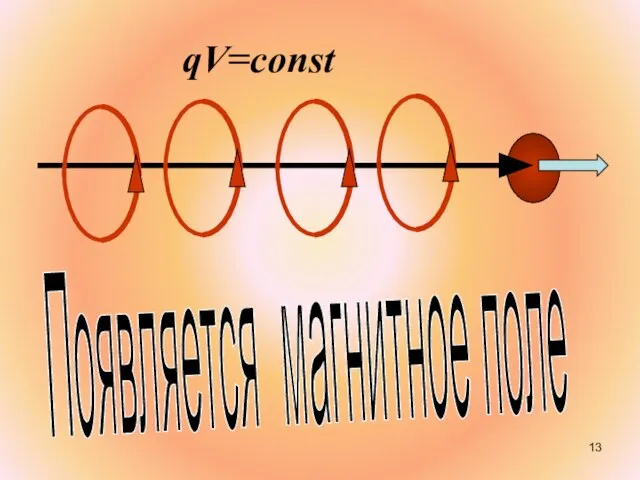
- 13. Появляется магнитное поле qV=const
- 14. т о к линия индукции магнитного поля Правило буравчика
- 15. Правило буравчика т о к направлен к нам линия индукции
- 16. Правило буравчика т о к направлен от нас линия индукции
- 17. Подобно электрическому полю, оно обладает энергией и, следовательно, массой. Магнитное поле материально. Теперь можно дать следующее
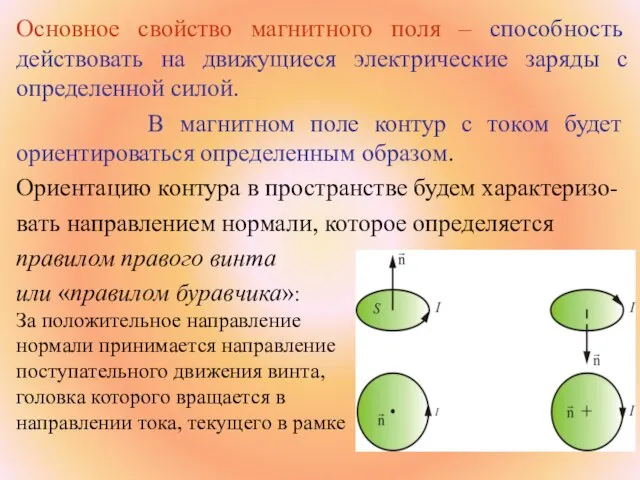
- 18. Основное свойство магнитного поля – способность действовать на движущиеся электрические заряды с определенной силой. В магнитном
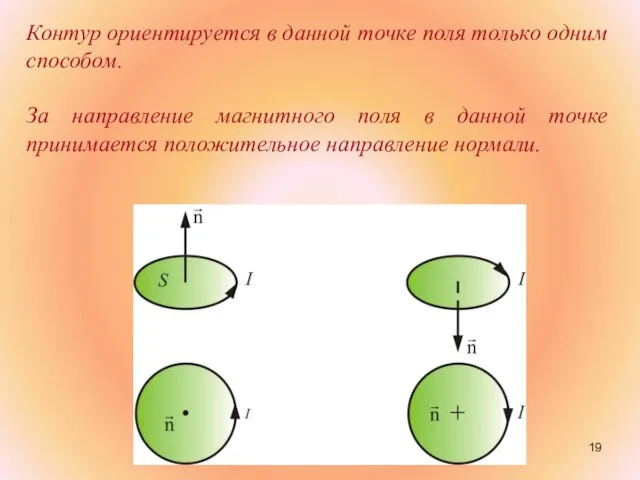
- 19. Контур ориентируется в данной точке поля только одним способом. За направление магнитного поля в данной точке
- 20. Вращающий момент прямо пропорционален величине тока I, площади контура S и синусу угла между направлением магнитного
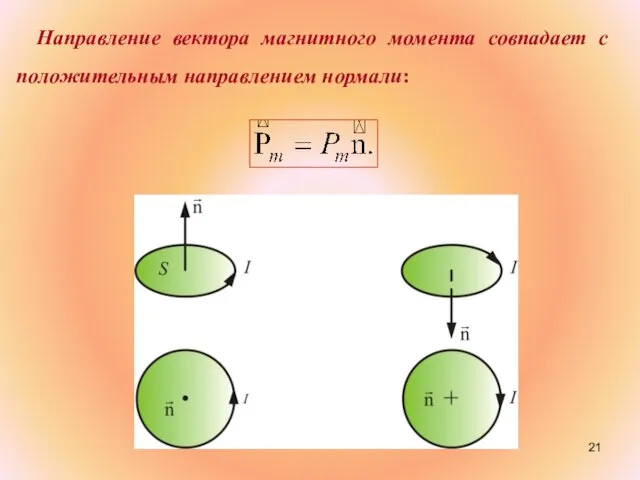
- 21. Направление вектора магнитного момента совпадает с положительным направлением нормали:
- 22. для данной точки магнитного поля будет одним и тем же и может служить характеристикой магнитного поля,
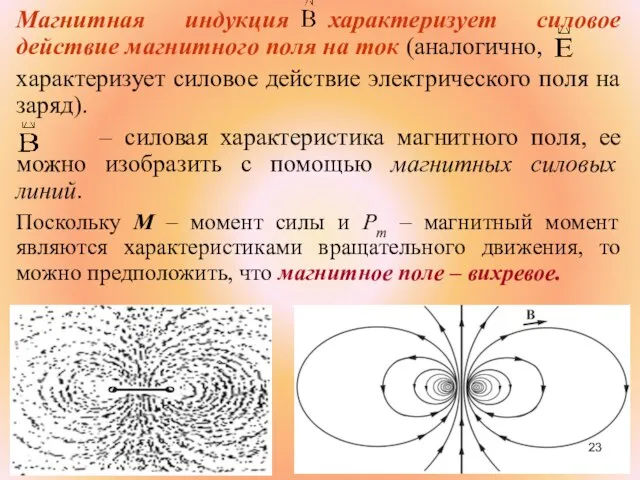
- 23. Магнитная индукция характеризует силовое действие магнитного поля на ток (аналогично, характеризует силовое действие электрического поля на
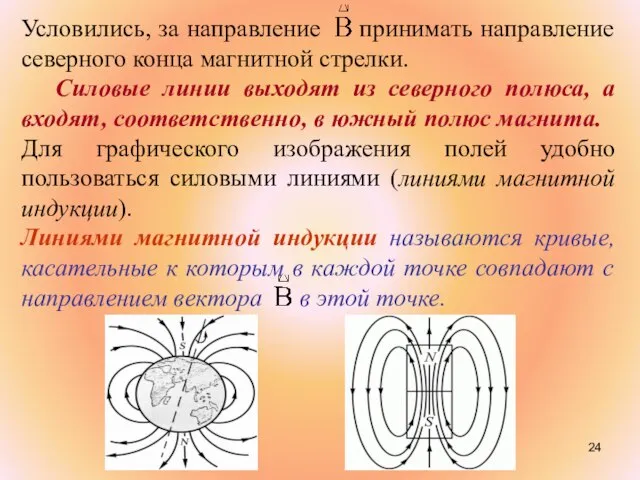
- 24. Условились, за направление принимать направление северного конца магнитной стрелки. Силовые линии выходят из северного полюса, а
- 25. Конфигурацию силовых линий легко установить с помощью мелких железных опилок которые намагничиваются в исследуемом магнитном поле
- 26. 1.2. 3акон Био–Савара–Лапласа В 1820 г. французские физики Жан Батист Био и Феликс Савар, провели исследования
- 27. Появляется магнитное поле qV=const
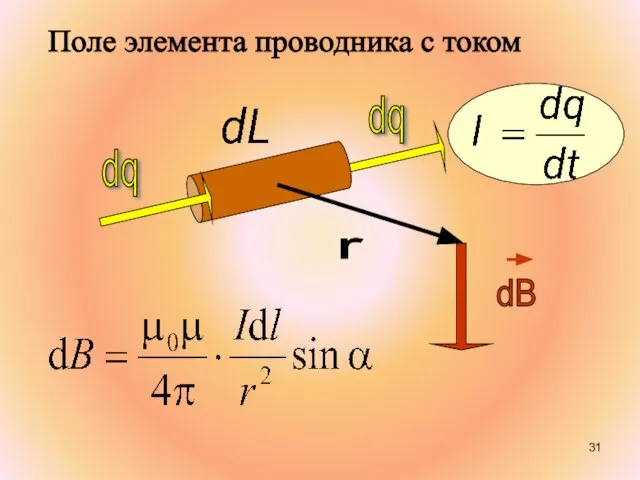
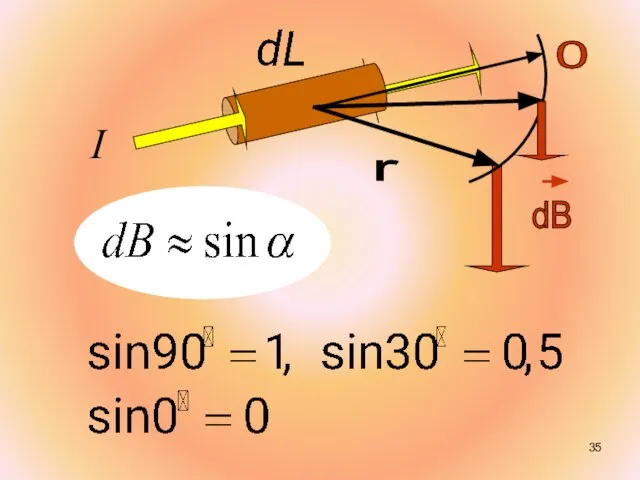
- 28. 3акон Био–Савара–Лапласа Элемент тока длины dl создает поле с магнитной индукцией: или в векторной форме:
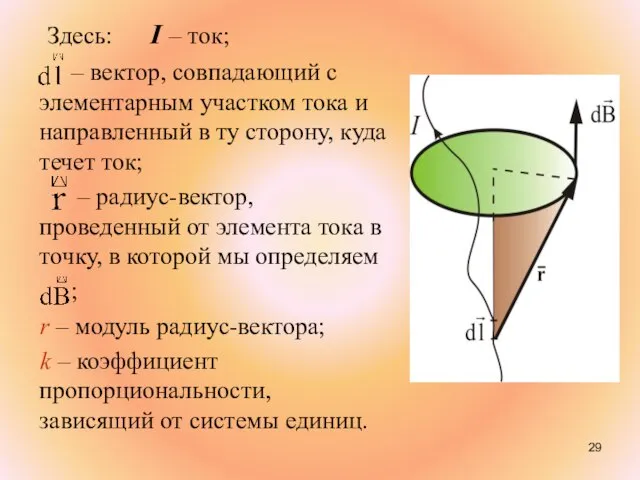
- 29. Здесь: I – ток; – вектор, совпадающий с элементарным участком тока и направленный в ту сторону,
- 30. Вектор магнитной индукции направлен перпендикулярно плоскости, проходящей через и точку, в которой вычисляется поле.
- 31. Поле элемента проводника с током
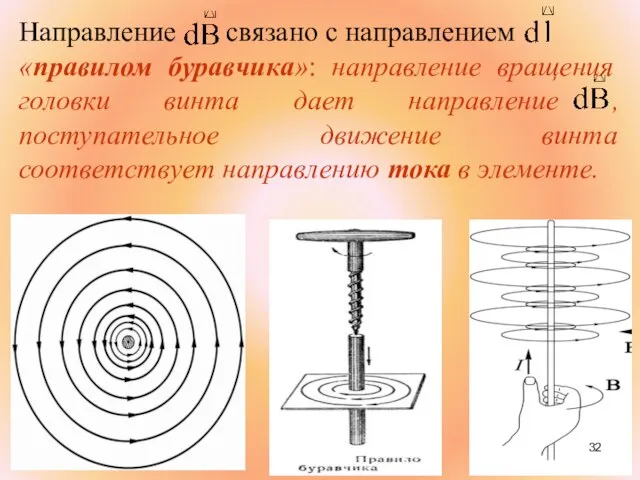
- 32. Направление связано с направлением «правилом буравчика»: направление вращения головки винта дает направление , поступательное движение винта
- 33. Закон Био–Савара–Лапласа устанавливает величину и направление вектора в произвольной точке магнитного поля, созданного проводником с током
- 34. где – магнитная постоянная. Закон Био–Савара–Лапласа для вакуума можно записать так:
- 35. I dB r 0
- 36. Магнитное поле любого тока может быть вычислено как векторная сумма (суперпозиция) полей, создаваемых отдельными элементарными участками
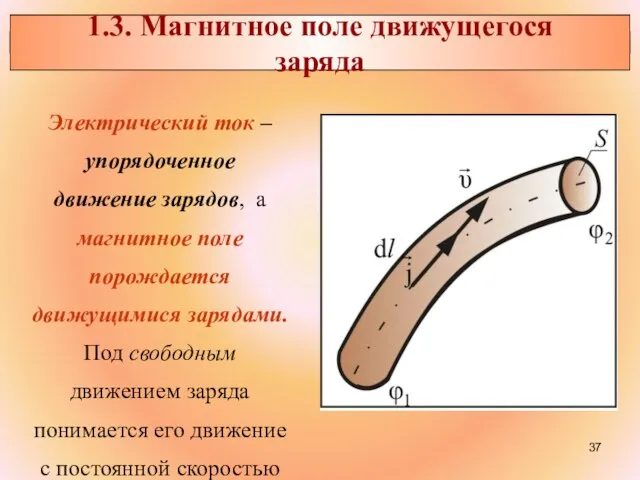
- 37. 1.3. Магнитное поле движущегося заряда Электрический ток – упорядоченное движение зарядов, а магнитное поле порождается движущимися
- 38. Индукция магнитного поля, создаваемого одним зарядом, движущимся со скоростью :
- 39. В скалярной форме индукция магнитного поля одного заряда в вакууме определяется по формуле: Эта формула справедлива
- 40. Магнитное поле – это одна из форм проявления электромагнитного поля, особенностью которого является то, что это
- 41. Магнитное поле создается проводниками с током, движущимися электрическими заряженными частицами и телами, а также переменными электрическими
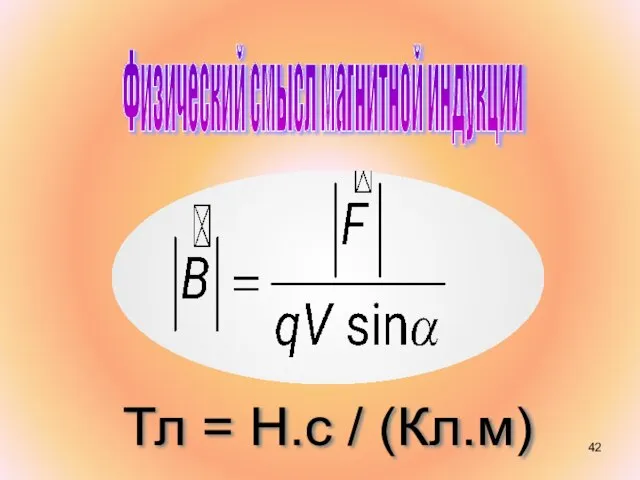
- 42. Физический смысл магнитной индукции ? Тл = Н.с / (Кл.м)
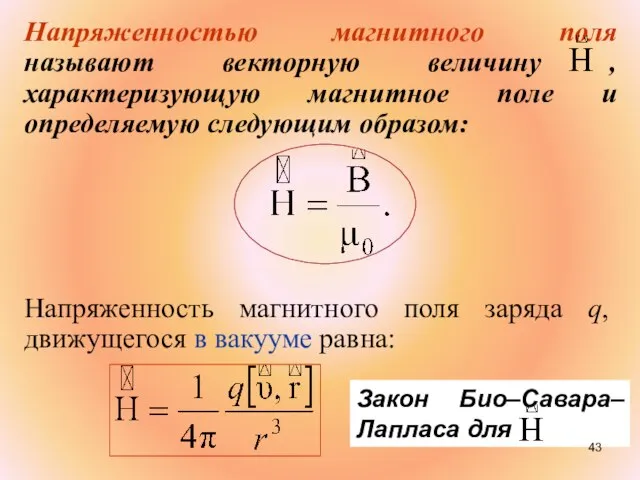
- 43. Напряженностью магнитного поля называют векторную величину , характеризующую магнитное поле и определяемую следующим образом: Напряженность магнитного
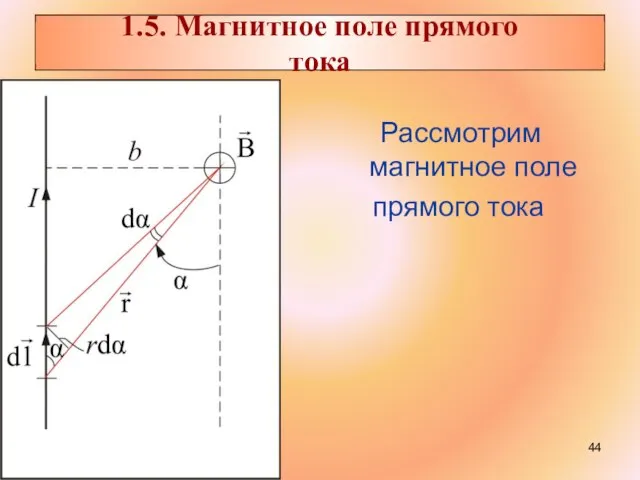
- 44. Рассмотрим магнитное поле прямого тока 1.5. Магнитное поле прямого тока
- 45. Пусть точка, в которой определяется магнитное поле, находится на расстоянии b от провода. Из рис. 1.6
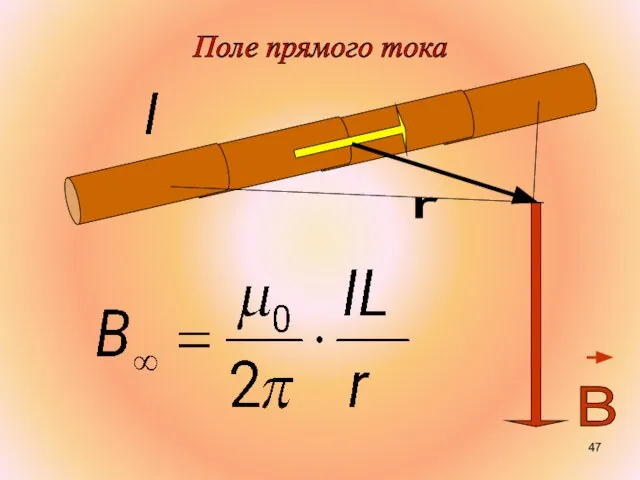
- 46. Для конечного проводника угол α изменяется от α1 до α2. Тогда: Для бесконечно длинного проводника α1
- 47. Поле прямого тока
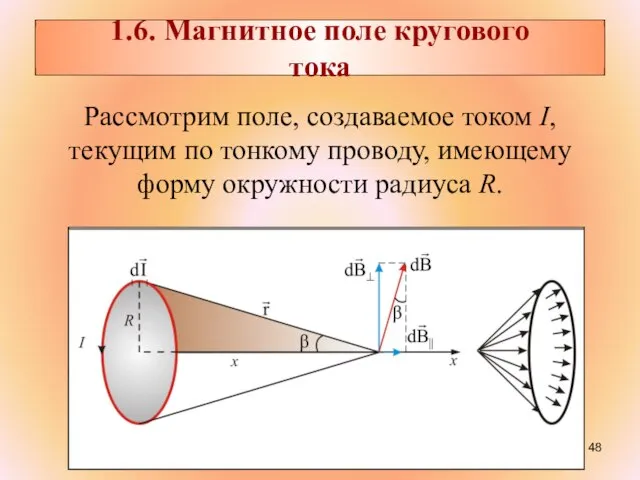
- 48. Рассмотрим поле, создаваемое током I, текущим по тонкому проводу, имеющему форму окружности радиуса R. 1.6. Магнитное
- 49. т.к. угол между и α – прямой, то тогда получим: (1.6.1)
- 50. Подставив в (1.6.1) и, проинтегрировав по всему контуру получим выражение для нахождения магнитной индукции кругового тока:
- 51. Поле кругового тока
- 52. Заметим, что в числителе (1.6.2) – магнитный момент контура. Тогда, на большом расстоянии от контура, при
- 53. Силовые линии магнитного поля кругового тока хорошо видны в опыте с железными опилками ( см. рис.).
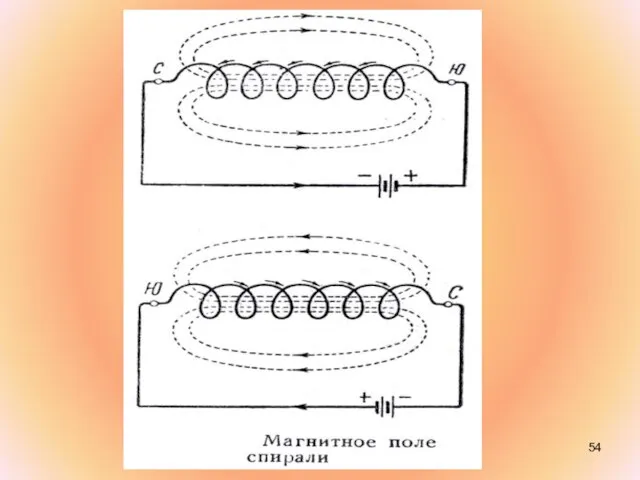
- 55. однородное поле Поле соленоида
- 56. Поток вектора через замкнутую поверхность должен быть равен нулю. Таким образом: Это теорема Гаусса для ФВ
- 57. α Определение потока вектора магнитной индукции dS
- 58. В природе нет магнитных зарядов – источников магнитного поля, на которых начинались и заканчивались бы линии
- 59. Магнитное поле обладает тем свойством, что его дивергенция всюду равна нулю: или Электростатического поля может быть
- 60. Основные уравнения магнитостатики Основные уравнения магнитостатики для магнитных полей, созданных постоянными потоками зарядов, записанные в дифференциальной
- 61. Магнитные линии образуют петли вокруг токов. Не имея ни конца, ни начала, линии В возвращаются в
- 63. Скачать презентацию



























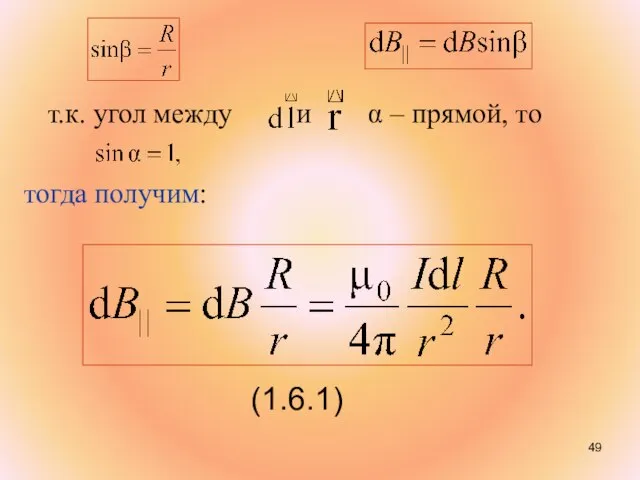

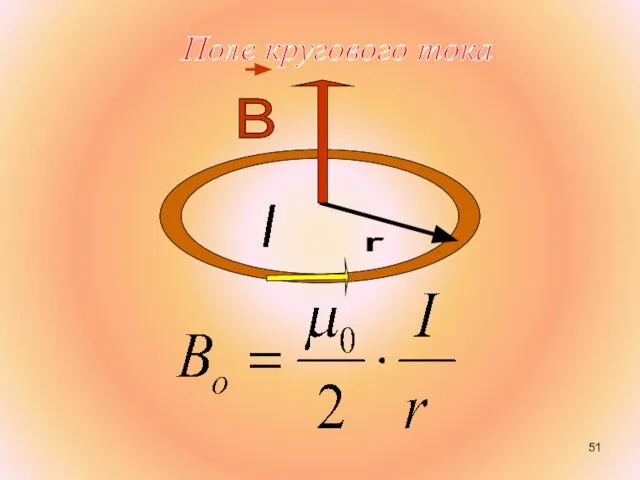









 Russian Rock Music: A Sociocultural Perspective
Russian Rock Music: A Sociocultural Perspective Православные храмы камчатского края
Православные храмы камчатского края Рисование клоуна с элементами аппликации
Рисование клоуна с элементами аппликации Правительственная программа «Английский язык для Республики Татарстан»
Правительственная программа «Английский язык для Республики Татарстан» Enchanté
Enchanté Фотосессия на День Святого Валентина
Фотосессия на День Святого Валентина Анализ и совершенствование рекламной деятельности гостиничного предприятия
Анализ и совершенствование рекламной деятельности гостиничного предприятия Склонение имён существительных в русском языке
Склонение имён существительных в русском языке Туристическое снаряжение
Туристическое снаряжение матиматикония
матиматикония Obstetrics and Gynecology
Obstetrics and Gynecology Презентация на тему Обеспечение
Презентация на тему Обеспечение Проект технічного оснащення м’ясопереробного підприємства
Проект технічного оснащення м’ясопереробного підприємства Презентация на тему профилактика курения
Презентация на тему профилактика курения  Тема: Реальдо Коломбо: описание циркуляции крови через лёгкие.
Тема: Реальдо Коломбо: описание циркуляции крови через лёгкие. Украинская АссоциацияИнтернет Рекламы
Украинская АссоциацияИнтернет Рекламы Новые организационно-правовые формы учреждений дополнительного образования
Новые организационно-правовые формы учреждений дополнительного образования Сертификаты соответствия на продукцию
Сертификаты соответствия на продукцию Информационно-справочная система Предприятие средств диспетчерского и технологического управления РУП Гродноэнерго
Информационно-справочная система Предприятие средств диспетчерского и технологического управления РУП Гродноэнерго Где логика? Интерактивная игра. Человеческие органы
Где логика? Интерактивная игра. Человеческие органы Осторожно: клещи
Осторожно: клещи ДП «Укрметртестстандарт» Науково-технічний семінар-нарада «Проблеми підвищення рівня метрологічного забезпечення вимірювань
ДП «Укрметртестстандарт» Науково-технічний семінар-нарада «Проблеми підвищення рівня метрологічного забезпечення вимірювань Предвыборная программа
Предвыборная программа Логические основы построения компьютера. Основные понятия алгебры логики Алгебра логики – это раздел математики, изучающий выск
Логические основы построения компьютера. Основные понятия алгебры логики Алгебра логики – это раздел математики, изучающий выск Нерентабельные салоны. Определение причин
Нерентабельные салоны. Определение причин Информационное обеспечение учебного процесса на основе портальных технологий
Информационное обеспечение учебного процесса на основе портальных технологий Портфолио. Биография
Портфолио. Биография На какую систему налогообложения перейти?
На какую систему налогообложения перейти?