Презентация на тему Фотоны

§§ Введение
02
1900, гипотеза Планка
Излучение и поглощение света
веществом происходит не непрерывно,
а конечными порциями или квантами
Для согласия с классической
термодинамикой и электродинамикой:
Проблему равновесного излучения с
классических позиций решить не удается.

03
при распространении свет ведет
себя подобно совокупности частиц
(световых квантов – фотонов)
1905, гипотеза Эйнштейна
λ = 623 нм (He-Ne лазер)
Пример.
= 3,19·10–19 Дж ≈ 2 эВ
Масса фотона в движении:
Энергия фотона:
= 3,55·10–36 кг

04
Импульс фотона
= 1,06·10–27 кг·м/с
При взаимодействии с веществом
фотоны могут рассеиваться,
испускаться и поглощаться.
Число фотонов не сохраняется, зато
должны выполняться законы сохранения импульса и энергии.

§§ Внешний фотоэффект
05
Фотоэффект – испускание электронов
веществом под действием света.
1905, А.Эйнштейн
Пусть поверхность металла освещается
монохроматическим светом с частотой ν
Электрон не может «поглотить» фотон
из-за закона сохранения МИ (спина).

06
A1 – потеря энергии
в объеме
Aвых – работа выхода
электрона (1,4–5 эВ)
Закон сохранения энергии
уравнение
Эйнштейна
для фотоэффекта

07
Существование красной границы:
Металл λmax, нм
Cs 686
K 560
Na 540
Li 521
Hg 273,5
Fe 262
Ag 261
Au 265
п/п λmax, нм
Ge 260
Si 258
УФ
Работа выхода, эВ
Cs 1,81
K,Na,Li 2,22–2,38
Hg…Au 4,55–4,75

08
Для прекращения эмиссии электронов
необходимо приложить задерживающую
разность потенциалов
Приложение ускоряющей разности
потенциалов используется в
фотоэлектронном умножителе
Ускоренные электроны могут вызвать
и свечение люминофора (приборы
ночного видения, тепловизоры)
KУ~106–108

Применение
09
1) Приёмники и усилители сигналов ЭМВ
в электрические сигналы (R, U, I)
2) Преобразователи ЭМВ ИК и УФ
в излучение видимого диапазона

10
Наблюдение объекта
через тепловизор
позволяет выявить
утечки, слабые места,
избежать аварии.

§§ Внутренний фотоэффект
11
В диэлектриках и полупроводниках электрон изменяет свою энергию не
выходя на поверхность.
У вещества изменяется проводимость (фоторезисторы).
В неоднородных полупроводниках также
наблюдается фотогальванический
эффект
– образование
разности потенциалов
под действием света.

Фотоэлементы (солнечные батареи)
в настоящее время используют как
источники электроэнергии
1) основа – кремний (Si)
2) КПД от 10 до 20%
3) Фото-ЭДС: 1–2 В
4) Фототок: ~0,01 А
с площади в 1 см2
(сотни ватт с 1 м2)
12

13
Фотоэффект применяют
в науке (измерения)
в технике:
усилители и преобразователи
организация электропитания
связь
контроль и управление

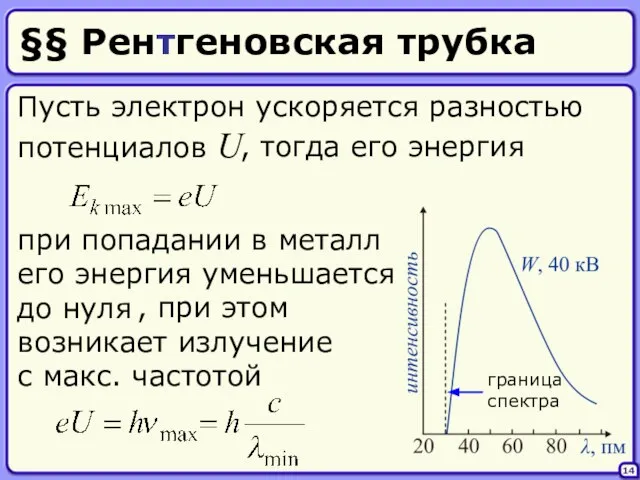
Пусть электрон ускоряется разностью
потенциалов U
§§ Рентгеновская трубка
14
, тогда его энергия
при попадании в металл
его энергия уменьшается
до нуля
, при этом
возникает излучение
с макс. частотой

§§ Эффект Комптона
15
1922–23 г., Артур Комптон
исследовал рассеяние рентгеновского
излучения на телах, состоящих из
легких атомов (графит, парафин).
Оказалось, что в рассеянном излучении
содержится две линии: λ и λ+Δλ
и не зависит от состава
тела и длины волны λ
Смещение

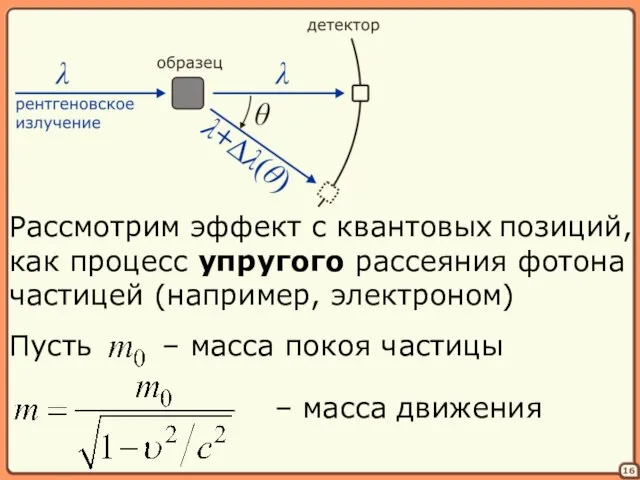
16
Рассмотрим эффект с квантовых позиций,
как процесс упругого рассеяния фотона
частицей (например, электроном)

17
λ – длина волны до рассеяния
λ1 – длина волны после рассеяния
Закон сохр. импульса (т.косинусов)
(1)

18
Закон сохранения энергии
(2)
Возведем в квадрат:

19
Вычтем: (1)–(2)

20
Если рассеяние происходит на электроне
– комптоновская длина волны электрона
Рассеяние происходит на случайный угол.
Если электрон не оторвется от атома,
то смещения по длине волны не будет.
Иногда наблюдается и обратный эффект
Комптона – уменьшение длины волны
у рассеянного излучения.

§§ Гипотеза Де Бройля
21
В оптических явлениях наблюдается
дуализм.
1924, Луи Де Бройль (Louis De Broglie)
гипотеза о всеобщем характере
корпускулярно-волнового дуализма
Это универсальное свойство природы
– всем микрообъектам присущи
одновременно и корпускулярные
и волновые свойства

Если двигается частица массой m со
скоростью υ
22
Энергия фотона:
Импульс фотона:
, то с частицей можно
ассоциировать волну с длиной
– длина волны
Де Бройля
Пример:
электрон, ускоренный разностью
потенциалов в 12 кВ
E = 12 кэВ = 1,92·10–15 Дж
λ = 10–10 м

23
Дифракция микрочастиц (электронов,
атомов и молекул)
наблюдается
аналогично дифракции рентгеновского
излучения
Для того, чтобы интерпретировать
явления интерференции и дифракции
микрочастиц
принимают, что
Интенсивность сопоставляемой волны
пропорциональна вероятности
обнаружения частицы в этой точке

Соотношение неопределённостей
24
В классической механике у каждой
частицы были свои координаты
и импульс
в каждый момент времени.
следует принцип неопределенности
Из формулы де Бройля

25
Пусть импульс частицы p нам известен
точно (Δp = 0)
, тогда волна,
ассоциированная с частицей – строго
монохроматическая
Это бесконечная sin волна, занимающая
все пространство (Δx = ∞)
Пусть частица локализована в области
пространства Δx = L.
Тогда ей соответствует волновой пакет
(набор волн, импульсов), т.е. Δp ≠ 0

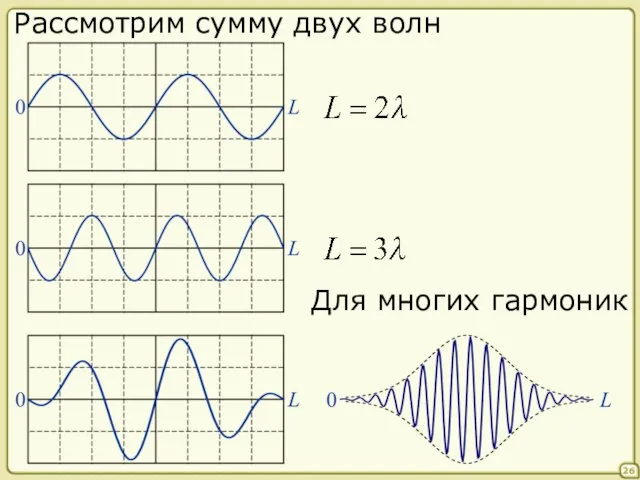
26
Рассмотрим сумму двух волн
Для многих гармоник

27
Пусть
и
тогда
или

28
Более строгое выражение называется
соотношением неопределенностей
Гейзенберга
Это означает, что в квантовой механике нет (не применимо) понятие траектории
частицы
Можно говорить лишь о вероятности
нахождения частицы в данной области
пространства.

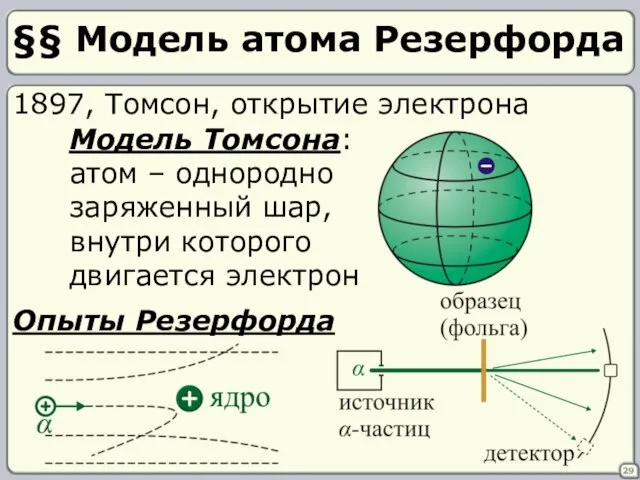
§§ Модель атома Резерфорда
29
1897, Томсон, открытие электрона
Модель Томсона:
атом – однородно
заряженный шар,
внутри которого
двигается электрон
Опыты Резерфорда

30
Ядерная модель атома
1) Атом – система зарядов, в центре
которой располагается тяжелое
положительно заряженное ядро
Q = Z|e|
dя ~ 10–14 – 10–15 м
2) вокруг ядра – Z электронов
dA ~ 10–10 м (несколько Å)
Трудности:
1) Система зарядов либо непрерывно
излучает энергию, либо неустойчива
3) Тождественность атомов
2) Линейчатый спектр

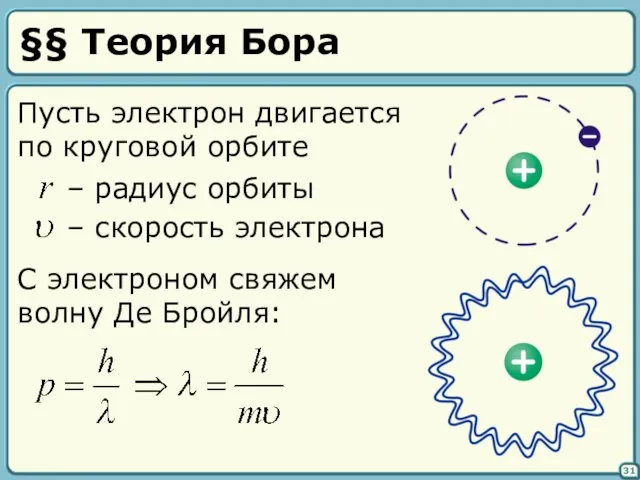
§§ Теория Бора
31
Пусть электрон двигается
по круговой орбите
С электроном свяжем
волну Де Бройля:

32
Пусть на длине окружности укладывается целое число длин волн (условие max):
т.е. момент импульса электрона на
орбите принимает только дискретные
значения (т.е. «квантуется»):
n = 1,2,3...– главное квантовое число

33
Заряд ядра атома:
Z – порядковый номер элемента
e = –1,6·10–19 Кл – заряд электрона
Сила, действующая на электрон
, k = 9·10–9 Н·м/Кл2
по II-му закону Ньютона

34
Получаем систему
ее решение
– скорость электрона
– радиус орбиты

35
Каждому значению главного квантового
числа n соответствует своя круговая
орбита и скорость электрона υn на ней:
0,53
2,12
4,77
8,49
2,2
1,1
0,73
0,55
Энергия электрона (дискретный спектр):

36
При переходе атома (Z = 1) из состояния
с главным квантовым числом n
в состояние с m испускается или
поглощается квант с энергией:
13,54 эВ = 2,2·10–18 Дж
, R = 2,06·1016 рад/с

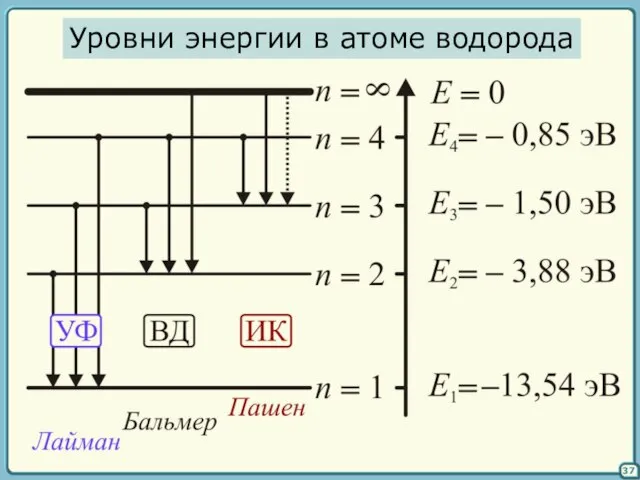
37
Уровни энергии в атоме водорода