Содержание
- 3. IV – V вв. до н.э. – ПИФАГОРЕЙСКАЯ ШКОЛА ПЕНТОГРАММА
- 4. М е ф и с т о ф е л ь: Нет, трудновато выйти мне теперь
- 5. Египетский
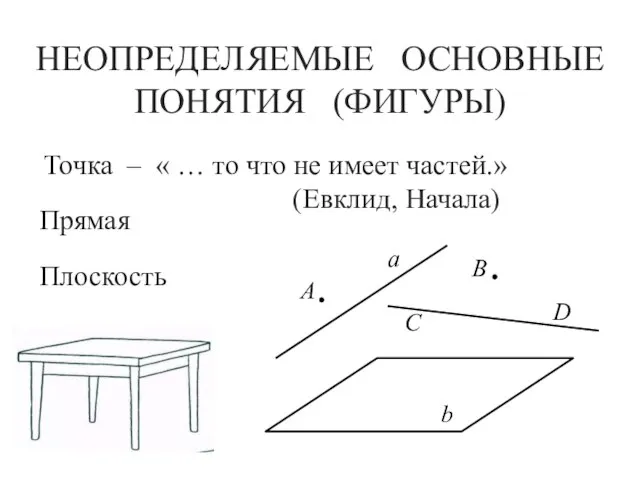
- 6. НЕОПРЕДЕЛЯЕМЫЕ ОСНОВНЫЕ ПОНЯТИЯ (ФИГУРЫ) Точка – « … то что не имеет частей.» (Евклид, Начала) Прямая
- 7. АКСИОМА (греч.) – достойное признания, не вызывающее сомнения. Основные свойства - аксиомы ДОКАЗАТЕЛЬСТВО ТЕОРЕМА
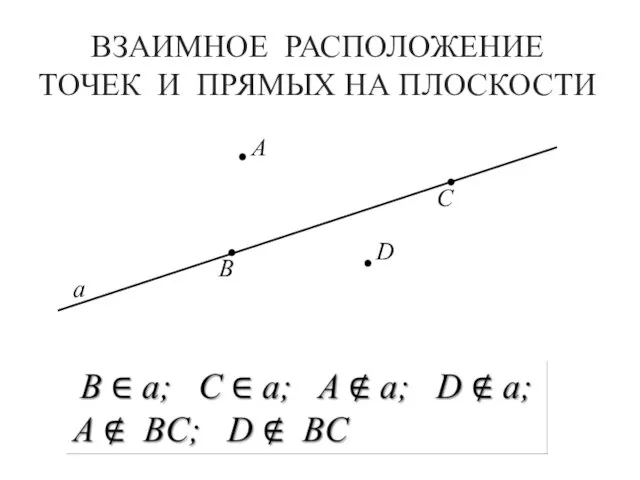
- 8. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ТОЧЕК И ПРЯМЫХ НА ПЛОСКОСТИ А B C D а
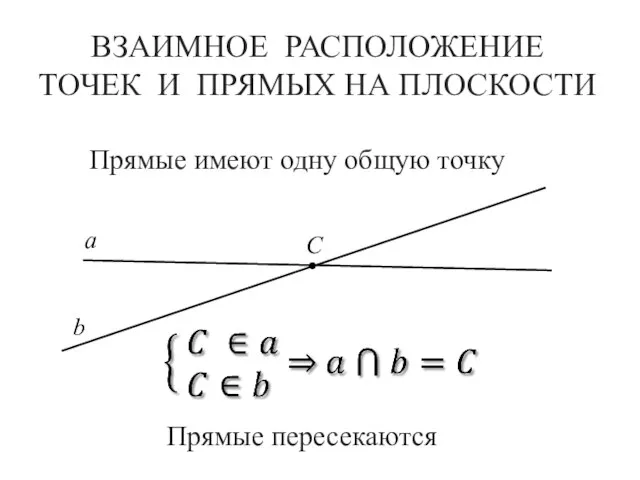
- 9. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ТОЧЕК И ПРЯМЫХ НА ПЛОСКОСТИ а b C Прямые пересекаются Прямые имеют одну общую
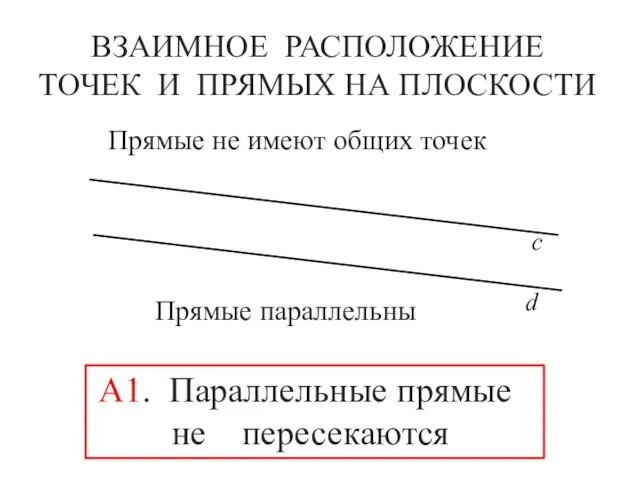
- 10. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ТОЧЕК И ПРЯМЫХ НА ПЛОСКОСТИ с d Прямые не имеют общих точек Прямые параллельны
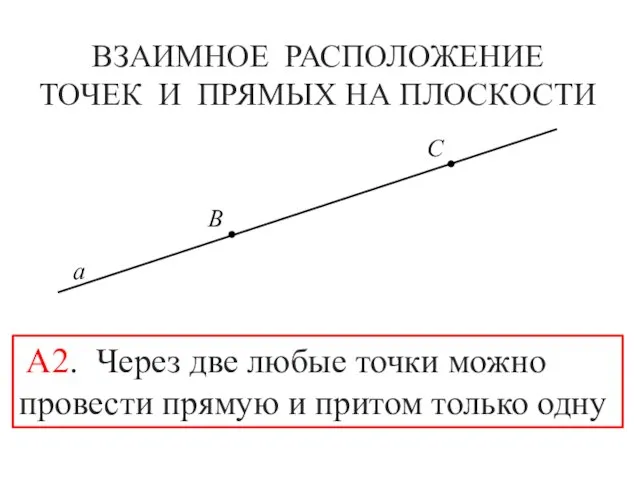
- 11. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ТОЧЕК И ПРЯМЫХ НА ПЛОСКОСТИ B C а А2. Через две любые точки можно
- 12. Провести четыре прямые так чтобы каждые две из них пересекались, но никакие три не пересекались в
- 13. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ТОЧЕК И ПРЯМЫХ НА ПЛОСКОСТИ Сколько прямых изображено? Сколько у них точек попарных пересечений?
- 14. Сколько прямых можно провести через а) три точки б) четыре точки Рассмотрите все возможные случаи. Выполните
- 16. Скачать презентацию







 RM_TravelExpo
RM_TravelExpo 08
08 Подведение итогов за II отчетный период международного проекта Государственного камерного хора Республики Мордовия «Духовно-нра
Подведение итогов за II отчетный период международного проекта Государственного камерного хора Республики Мордовия «Духовно-нра Для друга 2.0
Для друга 2.0 Инвестиции в будущее: поиск новых подходов в вопросах воспитания с учетом социального заказа и вызовов современности
Инвестиции в будущее: поиск новых подходов в вопросах воспитания с учетом социального заказа и вызовов современности Общеобразовательное учреждение с дополнительным образованием с участием социальных партнеров. Школа-интернат мужского воспитания
Общеобразовательное учреждение с дополнительным образованием с участием социальных партнеров. Школа-интернат мужского воспитания Художественный образ города Шатура
Художественный образ города Шатура Лес нужно защищать!
Лес нужно защищать! Презентация на тему Решение неравенств методом интервалов (9 класс)
Презентация на тему Решение неравенств методом интервалов (9 класс) 5 шагов к Soldout
5 шагов к Soldout Предварительные итоги трудоустройства выпускников БОУ СПО ВО «Вологодский педагогический колледж» в 2011 г.
Предварительные итоги трудоустройства выпускников БОУ СПО ВО «Вологодский педагогический колледж» в 2011 г.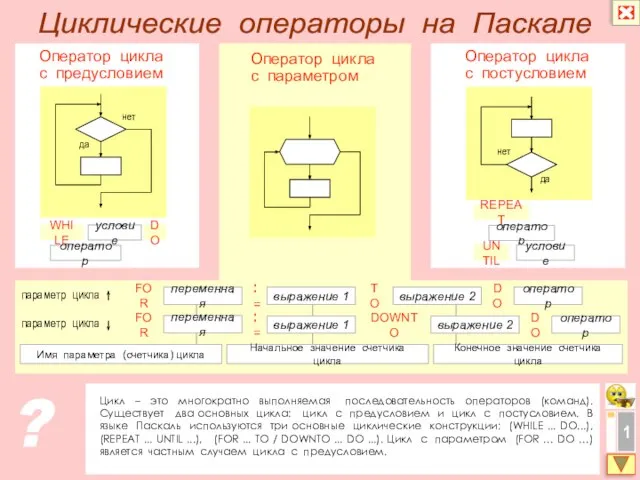 Циклические операторы на Паскале
Циклические операторы на Паскале Презентация на тему УРОКИ НРАВСТВЕННОСТИ
Презентация на тему УРОКИ НРАВСТВЕННОСТИ Презентация на тему Заповедник о.Врангеля
Презентация на тему Заповедник о.Врангеля Эволюция Российского герба
Эволюция Российского герба Как стать счастливым?
Как стать счастливым? Искусство эпохи Средневековья
Искусство эпохи Средневековья Safety monitoring the progress of construction of production
Safety monitoring the progress of construction of production ООО ВПСМ
ООО ВПСМ По страницам истории животного мира
По страницам истории животного мира Аналитический отчет
Аналитический отчет Турслёт в начальной школе
Турслёт в начальной школе Предложение
Предложение Судьба женщин и детей в годы Великой Отечественной войны
Судьба женщин и детей в годы Великой Отечественной войны ВОВЛЕЧЕННОСТЬ В YOTA
ВОВЛЕЧЕННОСТЬ В YOTA Будь здоров малыш
Будь здоров малыш Drush и Drupal
Drush и Drupal Преимущества программы «1С:Зарплата и Управление Персоналом 8» при переходе с «1С:Зарплата и Кадры 7.7»
Преимущества программы «1С:Зарплата и Управление Персоналом 8» при переходе с «1С:Зарплата и Кадры 7.7»