Презентация на тему ГИА 2017. Модуль АЛГЕБРА (№4)

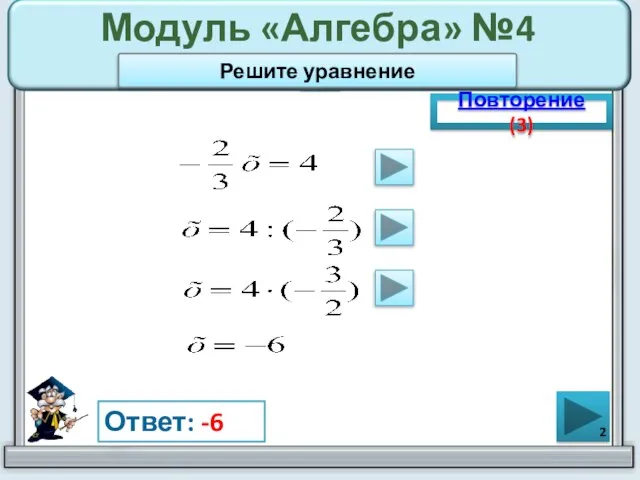
Модуль «Алгебра» №4
Повторение (3)
Ответ: -6
Решите уравнение

Повторение (подсказка)
В уравнении можно делить обе части уравнения на одно и то же число, не равное нулю.
Чтобы разделить число на обыкновенную дробь, надо первое число умножить на взаимно обратное дроби.
При умножении двух чисел в разными знаками результат будет отрицательным.

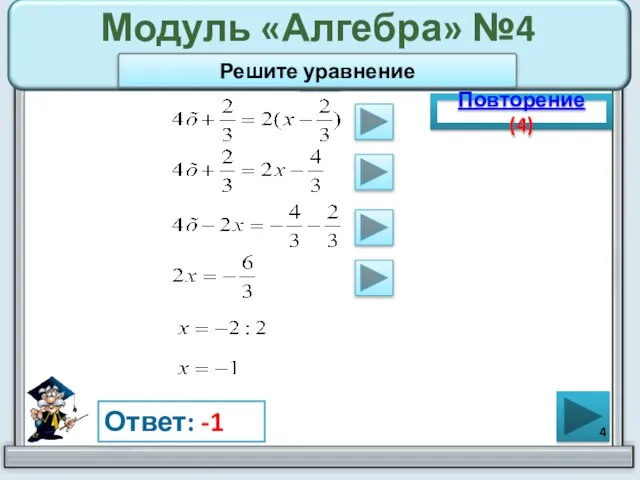
Модуль «Алгебра» №4
Повторение (4)
Ответ: -1
Решите уравнение

Повторение (подсказка)
Чтобы умножить число на скобку, надо число умножить на каждое слагаемое скобки.
При решении уравнения можно переносить слагаемые из одной части уравнения в другую, меняя знак слагаемых на противоположный.
Чтобы сложить дроби с одинаковыми знаменателями, надо сложить числители, а знаменателями оставить без изменения.
Сократить дробь, значит разделить и числитель, и знаменатель на одно и то же число.

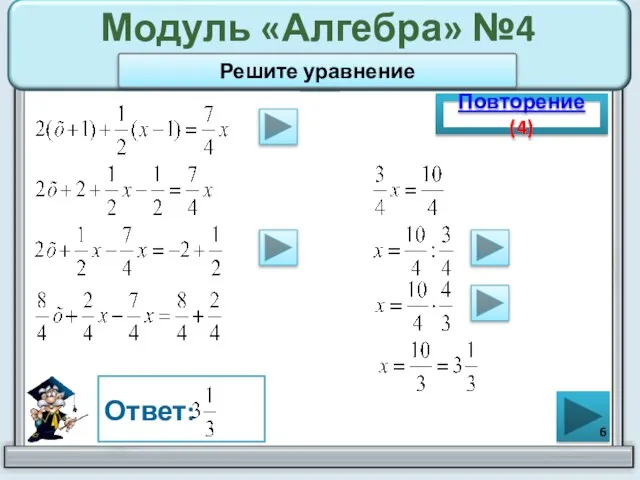
Модуль «Алгебра» №4
Повторение (4)
Ответ:
Решите уравнение

Повторение (подсказка)
Чтобы умножить одночлен на многочлен, надо одночлен умножить на каждый член многочлена.
Чтобы сложить (вычесть) дроби с разными знаменателями, надо привести дроби к общему знаменателю и сложить (вычесть) числители.
Чтобы умножить обыкновенные дроби, надо перемножить отдельно числители и знаменатели.
Чтобы выделить целую часть из неправильной дроби, надо числитель разделить на знаменатель, неполное частное – целая часть, остаток – числитель, знаменатель без изменения

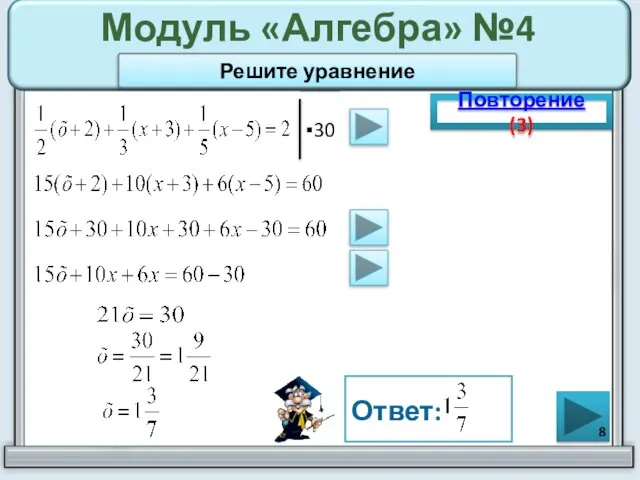
Модуль «Алгебра» №4
Повторение (3)
Ответ:
Решите уравнение
▪30

Повторение (подсказка)
Чтобы «избавиться» от дробей, надо уравнение почленно умножить на общий знаменатель дробей, входящих в уравнение.
Сумма противоположных чисел равна нулю.
Подобными слагаемыми называются те, которые имеют одинаковую буквенную часть или не имеют ее вовсе.

Модуль «Алгебра» №4
▪(2-х), где 2-х≠0; х≠2
Повторение (2)
Ответ:
Решите уравнение

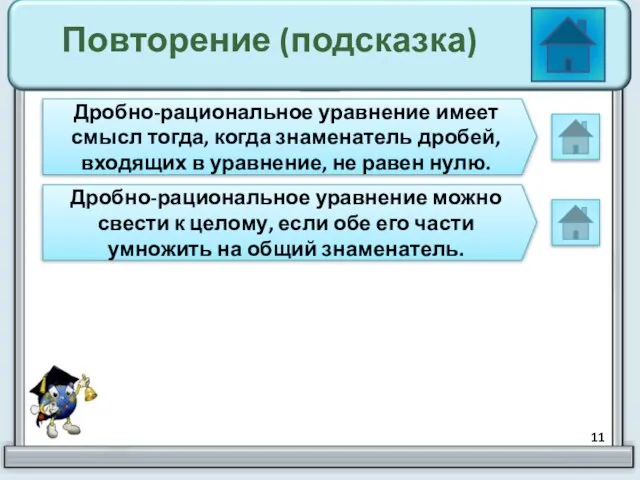
Повторение (подсказка)
Дробно-рациональное уравнение имеет смысл тогда, когда знаменатель дробей, входящих в уравнение, не равен нулю.
Дробно-рациональное уравнение можно свести к целому, если обе его части умножить на общий знаменатель.

Модуль «Алгебра» №4
Повторение (3)
Ответ: -13,5
Решите уравнение
Проверка:
если х=-3,25, то
верно

Повторение (подсказка)
В верной пропорции произведение крайних членов равно произведению средних членов.
Собираем подобные слагаемые, т.е. переносим их из одной части уравнения в другую, меняя их знаки на противоположные.
Если сложить числа с противоположными знаками, то надо из большего модуля вычесть меньший, поставив в ответе знак числа с большим модулем.

Модуль «Алгебра» №4
2
Повторение (4)
Ответ: 0,5; -4
Решите уравнение
D>0, ⇒ 2 корня

Повторение (подсказка)
Квадратным уравнением называется уравнение вида ax²+bx+c=0
Дискриминант – различитель можно найти по формуле
Так как D>0, то уравнение имеет два корня.
Корни квадратного уравнения можно вычислить по формулам:

Модуль «Алгебра» №4
Повторение (3)
Ответ: -5; 7.
Решите уравнение
⇒

Повторение (подсказка)
Если все числовые коэффициенты уравнения имеют общий делитель, то их можно сократить на этот делитель.
Приведенным называется квадратное уравнение, старший коэффициент которого равен единице.
Если числа х₁ и х₂ таковы, что х₁+х₂=-b, х₁∙х₂=с, то эти числа – корни уравнения
(обратная теорема Виета).

Модуль «Алгебра» №4
Решим систему методом подстановки:
Повторение (3)
Ответ: (2;4)
Решите систему уравнений

Повторение (подсказка)
Чтобы решить систему уравнений методом подстановки, надо вместо у во втором уравнении подставить 2х, и получим уравнение с одной переменной.
Чтобы найти значение второй переменной (у), надо в первое уравнение подставить вместо х значение равное 2 и решить получившееся уравнение.
Решение системы уравнений записывают парой чисел в виде координат точки.

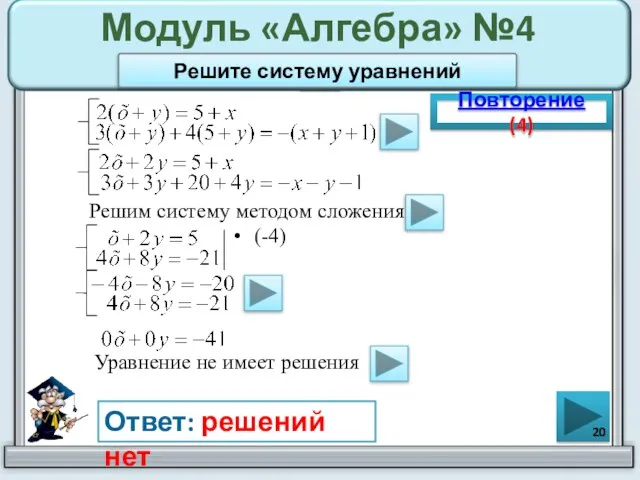
Модуль «Алгебра» №4
(-4)
Повторение (4)
Ответ: решений нет
Решите систему уравнений
Решим систему методом сложения
Уравнение не имеет решения

Повторение (подсказка)
Если пред скобкой стоит знак «минус», то при раскрытии скобок скобки и этот знак опускают, а знаки в скобках меняют на противоположные.
Умножить почленно каждое уравнение на такие множители, чтобы при одной из переменных получить противоположные коэффициенты.
Надо сложить почленно уравнения чтобы исключить одну из переменных (в данном случае х), и решить получившееся уравнение с одной переменной.
Если одно из уравнений не имеет решения, то и система не имеет решения.