Содержание
- 2. Уравнения состояния идеального газа Уравне́ние состоя́ния — уравнение, связывающее между собой термодинамические (макроскопические) параметры системы, такие,
- 3. С помощью модели идеального газа можно исследовать процессы, в которых масса газа и один из трех
- 4. Изотермический процесс. Закон Бойля - Мариотта . Для поддержания температуры газа постоянной необходимо, чтобы он мог
- 5. Роберт Бойль (1627 – 1691) — физик, химик и богослов, седьмой сын Ричарда Бойля, графа Коркского,
- 6. Изобарный процесс.Закон Гей-Люссака . Закон Гей-Люссака -закон зависимости объёма газа от абсолютной температуры при постоянном давлении
- 7. Жозе́ф Луи́ Гей-Люсса́к (1778 – 1850) — французский химик и физик, член Французской Академии наук (1806).
- 8. Изохорный процесс.Закон Шарля. Формулировка закона Шарля следующая: Давление газа фиксированной массы и фиксированного объёма прямо пропорционально
- 9. Жак Александр Сезар Шарль (1746 —1823) — французский изобретатель и учёный. Известен как изобретатель наполняемого водородом,
- 10. Изображение газовых законов в различных координатах
- 11. Другие виды процессов в идеальном газе Адиабатический процесс (изоэнтропийный). Термодинамический процесс, происходящий без теплообмена с окружающей
- 12. Клапейрон Бенуа Поль Эмиль (1799–1864) – французский физик и инженер. Физические исследования посвящены теплоте, пластичности и
- 13. Другие газовые законы. Закон Авогадро: При одинаковых давлениях и одинаковых температурах, в равных объёмах различных идеальных
- 14. Молекулярно-кинетическая теория (сокращённо МКТ) — теория XIX века, рассматривавшая строение вещества, в основном газов, с точки
- 15. Основное уравнение МКТ Задача молекулярно-кинетической теории состоит в том, чтобы установить связь между микроскопическими (масса, скорость,
- 16. Используя модель идеального газа, вычислим давление газа на стенку сосуда. В процессе взаимодействия молекулы со стенкой
- 17. Пусть в единице объема сосуда содержатся n молекул; тогда число молекул в объеме цилиндра равно nSυxΔt.
- 18. При выводе этого соотношения предполагалось, что все n молекул, содержащихся в единице объема газа, имеют одинаковые
- 19. Максвелл в 1860 г. вывел закон распределения молекул газа по скоростям, исходя из основных положений молекулярно-кинетической
- 20. Так как все направления для векторов скоростей молекул равновероятны, среднее значение квадратов их проекций на координатные
- 21. Возникают вопросы: каким образом можно на опыте изменять среднюю кинетическую энергию движения молекул в сосуде неизменного
- 22. Сравнивая соотношения p = nkT с основным уравнением молекулярно-кинетической теории газов, можно получить: Средняя кинетическая энергия
- 23. Задание. По графику изменения состояния идеального газа в координатах (p,T) изобразить изменение его состояния в координатах
- 24. Задание Углекислый газ объемом 1 л при нормальных условиях имеет массу 1,977 г. Какой реальный объем
- 26. Скачать презентацию
Слайд 2Уравнения состояния идеального газа
Уравне́ние состоя́ния — уравнение, связывающее между собой термодинамические (макроскопические) параметры
Уравнения состояния идеального газа
Уравне́ние состоя́ния — уравнение, связывающее между собой термодинамические (макроскопические) параметры

Идеальный газ — математическая модель газа, в которой предполагается, что потенциальной энергией взаимодействия молекул можно пренебречь по сравнению с их кинетической энергией.
Между молекулами не действуют силы притяжения или отталкивания, соударения частиц между собой и со стенками сосуда абсолютно упруги, а время взаимодействия между молекулами пренебрежимо мало по сравнению со средним временем между столкновениями.
Модель идеального газа широко применяется для решения задач термодинамики газов и задач аэрогазодинамики. Например, воздух при атмосферном давлении и комнатной температуре с большой точностью описывается данной моделью. В случае экстремальных температур или давлений требуется применение более точной модели, например модели газа Ван-дер-Ваальса, в котором учитывается притяжение между молекулами.
Слайд 3С помощью модели идеального газа можно исследовать процессы, в которых масса газа
С помощью модели идеального газа можно исследовать процессы, в которых масса газа

Процессы, протекающие при неизменном значении одного из параметров, называют изопроцессами (от греческого слова «изос» - равный). Правда, в действительности ни один процесс не может протекать при строго фиксированном значении какого-либо параметра. Всегда имеются те или иные воздействия, нарушающие постоянство температуры, давления или объема. Лишь в лабораторных условиях удается поддерживать постоянство того или иного параметра с высокой точностью, но в действующих технических устройствах и в природе это практически неосуществимо. Изопроцесс - это идеализированная модель реального процесса, которая только приближенно отражает действительность.
Слайд 4Изотермический процесс. Закон Бойля - Мариотта .
Для поддержания температуры газа постоянной необходимо,
Изотермический процесс. Закон Бойля - Мариотта .
Для поддержания температуры газа постоянной необходимо,
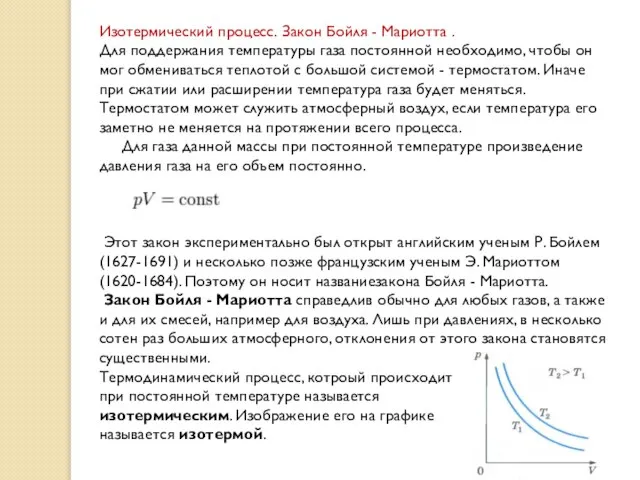
Этот закон экспериментально был открыт английским ученым Р. Бойлем (1627-1691) и несколько позже французским ученым Э. Мариоттом (1620-1684). Поэтому он носит названиезакона Бойля - Мариотта. Закон Бойля - Мариотта справедлив обычно для любых газов, а также и для их смесей, например для воздуха. Лишь при давлениях, в несколько сотен раз больших атмосферного, отклонения от этого закона становятся существенными.
Термодинамический процесс, котроый происходит
при постоянной температуре называется
изотермическим. Изображение его на графике
называется изотермой.
Слайд 5Роберт Бойль (1627 – 1691) — физик, химик и богослов, седьмой сын Ричарда
Роберт Бойль (1627 – 1691) — физик, химик и богослов, седьмой сын Ричарда

Участвовал в основании Общества наук, которое потом в 1668 г. переместилось в Лондон, а впоследствии под названием Лондонского королевского общества получило большую известность.
Эдм Мариотт (1620—1684) был настоятелем монастыря Сен-Мар-Тэнсубон в Дижоне (Франция). Одним из первых в 1666 г. он вошел в состав только что сформированной в том же году Французской Академии наук. Его эксперименты с воздухом привели к открытию ныне широко известного закона Бойля—Мариотта.
Слайд 6Изобарный процесс.Закон Гей-Люссака .
Закон Гей-Люссака -закон зависимости объёма газа от абсолютной температуры при
Изобарный процесс.Закон Гей-Люссака .
Закон Гей-Люссака -закон зависимости объёма газа от абсолютной температуры при

Закон Гей-Люссака утверждает, что при постоянном давлении объём постоянной массы газа пропорционален абсолютной температуре.
Однако сам Гей-Люссак считал, что открытие было сделано Жаком Шарлем в неопубликованной работе, относящейся к 1787 году. Независимо от них закон был открыт в 1801 году английским физиком Джоном Дальтоном. Кроме того, качественно закон был описан французом Гийомом Амонтоном в конце XVII века.
Графически эта зависимость в координатах V-T
изображается в виде прямой, выходящей из точки Т=0.
Эту прямую называют изобарой.
Процесс изменения состояния термодинамической
системы при постоянном давлении называют
изобарным (от греческого слова «барос» - вес ).
Слайд 7Жозе́ф Луи́ Гей-Люсса́к (1778 – 1850) — французский химик и физик, член Французской
Жозе́ф Луи́ Гей-Люсса́к (1778 – 1850) — французский химик и физик, член Французской

Большинство современников отмечают чрезвычайную честность Гей-Люссака как человека и как учёного. Он был суров и требователен и к себе самому, и к своим сослуживцам, и к научным оппонентам, невзирая на заслуги и регалии последних. Он всегда считал своей обязанностью признавать и публиковать собственные ошибки и заблуждения, если таковые обнаруживались.
Другой характерной чертой Гей-Люссака было личное бесстрашие, которое проявлялось как при проведении опасных научных экспериментов, так и в защите своих близких и коллег от политических репрессий и цензуры.
Например в 1804 году Гей-Люссак предпринял подъём на воздушном шаре с целью определить зависимость магнитного поля Земли и температуры атмосферы от высоты подъёма.
Слайд 8Изохорный процесс.Закон Шарля.
Формулировка закона Шарля следующая:
Давление газа фиксированной массы и фиксированного объёма
Изохорный процесс.Закон Шарля.
Формулировка закона Шарля следующая:
Давление газа фиксированной массы и фиксированного объёма

Закон давления, описанный выше, должен быть на самом деле приписан Гильому Амонтону, который в конце XVII века (точнее между 1700 и 1702 годом) обнаружил, что давление фиксированной массы газа, поддерживаемого при постоянном объёме, пропорционально его температуре. Амонтон обнаружил это при постройке «воздушного термометра».
Графически эта зависимость в координатах P-T
изображается в виде прямой, выходящей из
точки Т=0. Эту прямую называют изохорой.
Разным объемам соответствуют разные изохоры.
Процесс изменения состояния термодинамической
системы при постоянном объеме называют
изохорным (от греческого слова
«хорема»-вместимость).
Слайд 9Жак Александр Сезар Шарль (1746 —1823) — французский изобретатель и учёный. Известен как изобретатель
Жак Александр Сезар Шарль (1746 —1823) — французский изобретатель и учёный. Известен как изобретатель

Амонтон Гийом (1663 - 1705) — французский механик и физик, член Французской академии наук, один из пионеров трибологии.
С рождения Гильом был практически глух, поэтому никогда не посещал университетов и математику, физику, геодезию, прикладную и небесную механику, а также архитектуру и рисование Амонтон Гильом изучал самостоятельно.
Известен, разработчик закона Амонтона — Кулона.
Также Амонтон известен, как изобретатель: в 1677 году он создаёт гигрометр, в 1702 году им был создан барометр с U-образной трубкой.
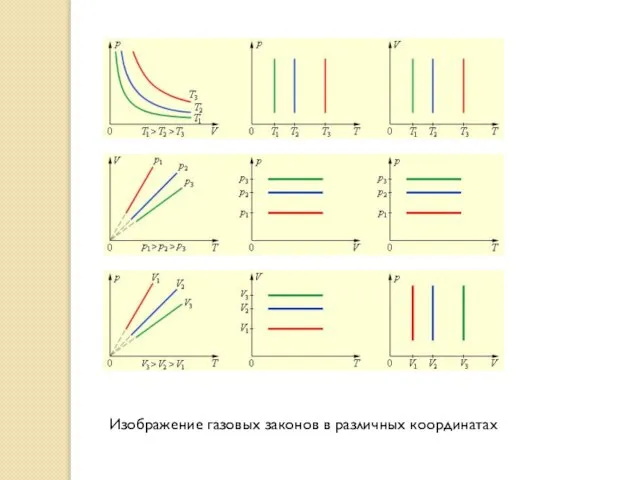
Слайд 10Изображение газовых законов в различных координатах
Изображение газовых законов в различных координатах
Слайд 11Другие виды процессов в идеальном газе
Адиабатический процесс (изоэнтропийный). Термодинамический процесс, происходящий без
Другие виды процессов в идеальном газе
Адиабатический процесс (изоэнтропийный). Термодинамический процесс, происходящий без

Политропический процесс. Процесс, при котором теплоёмкость газа остаётся постоянной. Политропический процесс – общий случай всех перечисленных выше процессов.
Объединённый газовый закон (закон Менделеева-Клапейрона).
Уравнение состояния идеального газа (иногда уравнение Клапейрона или уравнение Менделеева — Клапейрона) — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид:
Последнее уравнение называют объединённым газовым законом. Из него получаются законы Бойля — Мариотта, Шарля и Гей-Люссака.
Слайд 12Клапейрон Бенуа Поль Эмиль (1799–1864) – французский физик и инженер. Физические исследования
Клапейрон Бенуа Поль Эмиль (1799–1864) – французский физик и инженер. Физические исследования

Уравнение, выведенное Клапейроном, содержало некую неуниверсальную газовую постоянную r, значение которой необходимо было измерять для каждого газа:
Дми́трий Ива́нович Менделе́ев (1834- 1907) — русский учёный-энциклопедист: химик , физикохимик, физик, метролог, экономист, технолог, геолог, метеоролог, педагог, воздухоплаватель, приборостроитель. Профессор Санкт-Петербургского университета.
Менделеев обнаружил, что r прямо пропорциональна количеству вещества, коэффициент пропорциональности R он назвал универсальной газовой постоянной:
R = 8,314 Дж / (К * моль)
Слайд 13Другие газовые законы.
Закон Авогадро: При одинаковых давлениях и одинаковых температурах, в равных
Другие газовые законы.
Закон Авогадро: При одинаковых давлениях и одинаковых температурах, в равных

Моль любого вещества в газообразном состоянии при одинаковых температурах и давлениях занимает один и тот же объем. Как показали эксперименты, при нормальных условиях (р=1 атм(760 мм.рт.ст.), T=273K(Т=О С)) он равен 22,414 л.
Закон Дальтона. Давление смеси идеальных газов равно сумме парциальных давлений Р, входящих в неё газов:
Парциальное давление Pn – давление, которое оказывал бы данный газ, если бы он один занимал весь объем.
Для смеси двух газов:
Слайд 14Молекулярно-кинетическая теория (сокращённо МКТ) — теория XIX века, рассматривавшая строение вещества, в основном
Молекулярно-кинетическая теория (сокращённо МКТ) — теория XIX века, рассматривавшая строение вещества, в основном

все тела состоят из частиц: атомов, молекул и ионов;
частицы находятся в непрерывном хаотическом движении (тепловом);
частицы взаимодействуют друг с другом путём абсолютно упругих столкновений.
Началом становления МКТ послужила теория М. В. Ломоносова, который опытным путём опроверг теории о теплороде и флогистоне, подготовив тем самым, молекулярно-кинетическую теорию XIX века Рудольфа Клаузиуса, Людвига Больцмана и Джеймса Максвелла.
Флогисто́н (от греч. φλογιστός — горючий, воспламеняемый) — в истории химии — гипотетическая «сверхтонкая материя» — «огненная субстанция», якобы наполняющая все горючие вещества и высвобождающаяся из них при горении. Введён в начале XVIII века Иоганном Бехером и Георгом Шталем в 1703 году для объяснения процессов горения.
Теплоро́д — по распространённым в XVIII — начале XIX века воззрениям, невесомый флюид, присутствующий в каждом теле и являющийся причиной тепловых явлений. Введён в 1783 году Лавуазье.
Слайд 15Основное уравнение МКТ
Задача молекулярно-кинетической теории состоит в том, чтобы установить связь между
Основное уравнение МКТ
Задача молекулярно-кинетической теории состоит в том, чтобы установить связь между

В результате каждого столкновения между молекулами и молекул со стенками скорости молекул могут изменяться по модулю и по направлению; на интервалах времени между последовательными столкновениями молекулы движутся равномерно и прямолинейно. В модели идеального газа предполагается, что все столкновения происходят по законам упругого удара, т. е. подчиняются законам механики Ньютона.
Слайд 16Используя модель идеального газа, вычислим давление газа на стенку сосуда. В процессе
Используя модель идеального газа, вычислим давление газа на стенку сосуда. В процессе
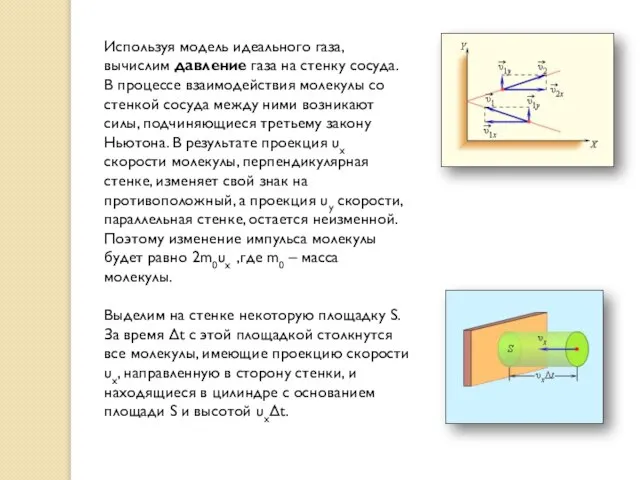
Выделим на стенке некоторую площадку S. За время Δt с этой площадкой столкнутся все молекулы, имеющие проекцию скорости υx, направленную в сторону стенки, и находящиеся в цилиндре с основанием площади S и высотой υxΔt.
Слайд 17Пусть в единице объема сосуда содержатся n молекул; тогда число молекул в
Пусть в единице объема сосуда содержатся n молекул; тогда число молекул в

½ nSυxΔt.
Поскольку каждая молекула при столкновении со стенкой изменяет свой импульс на величину 2m0υx , то полное изменение импульса всех молекул, столкнувшихся за время Δt с площадкой S, равно
2m0υx * ½ nSυxΔt = m0nSυx2Δt.
По законам механики это изменение импульса всех столкнувшихся со стенкой молекул происходит под действием импульса силы FΔt, где F – некоторая средняя сила, действующая на молекулы со стороны стенки на площадке S. Но по 3-му закону Ньютона такая же по модулю сила действует со стороны молекул на площадку S. Поэтому можно записать:
FΔt= nm0Sυx2Δt,
откуда
p=F/S= nm0υx2
Слайд 18При выводе этого соотношения предполагалось, что все n молекул, содержащихся в единице
При выводе этого соотношения предполагалось, что все n молекул, содержащихся в единице

В результате многочисленных соударений молекул газа между собой и со стенками в сосуде, содержащем большое число молекул, устанавливается некоторое статистическое распределение молекул по скоростям. При этом все направления векторов скоростей молекул оказываются равноправными (равновероятными), а модули скоростей и их проекции на координатные оси подчиняются определенным закономерностям. Распределение молекул газа по модулю скоростей называется распределением Максвелла.
Джеймс Клерк Ма́ксвелл (1831— 1879) — британский физик, математик и механик. Максвелл заложил основы современной классической электродинамики (уравнения Максвелла).
Один из основателей кинетической теории газов (установил распределение молекул газа по скоростям).
Слайд 19Максвелл в 1860 г. вывел закон распределения молекул газа по скоростям, исходя из основных
Максвелл в 1860 г. вывел закон распределения молекул газа по скоростям, исходя из основных
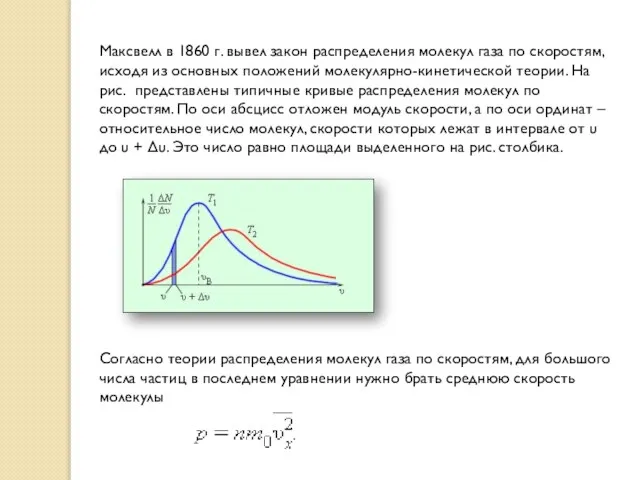
Согласно теории распределения молекул газа по скоростям, для большого числа частиц в последнем уравнении нужно брать среднюю скорость молекулы
Слайд 20Так как все направления для векторов скоростей молекул равновероятны, среднее значение квадратов
Так как все направления для векторов скоростей молекул равновероятны, среднее значение квадратов

Тогда формула для среднего давления газа на стенку сосуда запишется в виде
Это уравнение устанавливает связь между давлением p идеального газа, массой молекулы m0, концентрацией молекул n, средним значением квадрата скорости и средней кинетической энергией поступательного движения молекул. Его называют основным уравнением молекулярно-кинетической теории газов.
Таким образом, давление газа равно двум третям средней кинетической энергии поступательного движения молекул, содержащихся в единице объема.
Слайд 21Возникают вопросы: каким образом можно на опыте изменять среднюю кинетическую энергию движения
Возникают вопросы: каким образом можно на опыте изменять среднюю кинетическую энергию движения

Опыт показывает, что такой величиной является температура.
Понятие температуры тесно связано с понятием теплового равновесия. Тела, находящиеся в контакте друг с другом, могут обмениваться энергией. Энергия, передаваемая одним телом другому при тепловом контакте, называется количеством теплоты.
Из газовых законов следует, что давление разреженного газа в сосуде постоянного объема V изменяется прямо пропорционально его абсолютной температуре: p ~ T.
или
p = nkT
где k = R/NA =1,38·10–23 Дж/К –постоянная Больцмана
Слайд 22Сравнивая соотношения p = nkT с основным уравнением молекулярно-кинетической теории газов, можно получить:
Средняя кинетическая
Сравнивая соотношения p = nkT с основным уравнением молекулярно-кинетической теории газов, можно получить:
Средняя кинетическая

Таким образом, температура есть мера средней кинетической энергии поступательного движения молекул.
Следует обратить внимание на то, что средняя кинетическая энергия поступательного движения молекулы не зависит от ее массы. Броуновская частица, взвешенная в жидкости или газе, обладает такой же средней кинетической энергией, как и отдельная молекула, масса которой на много порядков меньше массы броуновской частицы.
Слайд 23Задание.
По графику изменения состояния идеального газа в координатах (p,T) изобразить изменение его
Задание.
По графику изменения состояния идеального газа в координатах (p,T) изобразить изменение его
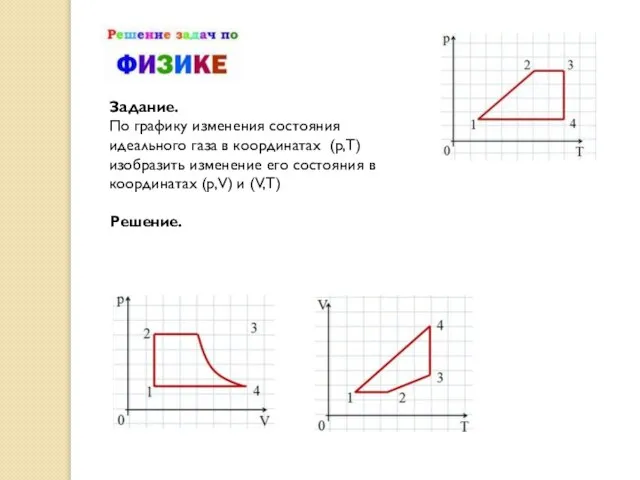
Решение.
Слайд 24Задание
Углекислый газ объемом 1 л при нормальных условиях имеет массу 1,977 г.
Задание
Углекислый газ объемом 1 л при нормальных условиях имеет массу 1,977 г.

Решение. Молярная масса М (CO2) = 44 г/моль, тогда объем моля 44/1,977 = 22,12 (л). Эта величина меньше принятой для идеальных газов (22,4 л).
Уменьшение объема связано с возрастанием взаимо действия между молекулами СО2, т. е. отклонением от идеальности.
 Презентация на тему Внедрение ФГОС в ДОУ
Презентация на тему Внедрение ФГОС в ДОУ  Келдыш Мстислав Всеволодович– советский учёный в области математики, механики, космической науки и техники, организатор науки, а
Келдыш Мстислав Всеволодович– советский учёный в области математики, механики, космической науки и техники, организатор науки, а Tierrechte: Vor- und Nachteile
Tierrechte: Vor- und Nachteile «Чудо в глазах наших»
«Чудо в глазах наших» Олимпиада үрләренә - баскычлап
Олимпиада үрләренә - баскычлап Бюджетная система РФ
Бюджетная система РФ Игра в «Съедобное и несъедобное»
Игра в «Съедобное и несъедобное» Colourful Grammar Цветная грамматика
Colourful Grammar Цветная грамматика  Презентация на тему Башни Московского кремля
Презентация на тему Башни Московского кремля Города-миллионеры Японии
Города-миллионеры Японии Интерактивная игра «Юным умникам» создана по аналогии игры "Своя игра" предназначена для обобщения и систематизации знаний по пре
Интерактивная игра «Юным умникам» создана по аналогии игры "Своя игра" предназначена для обобщения и систематизации знаний по пре Закрепление настенных предметов
Закрепление настенных предметов Московский городской педагогический университет
Московский городской педагогический университет Китайська лірика
Китайська лірика  Пословица недаром молвится
Пословица недаром молвится Презентация на тему Холодные блюда из рыбы
Презентация на тему Холодные блюда из рыбы Проект «Интересное рисование»
Проект «Интересное рисование» Презентация на тему Ознакомление с окружающим миром: зимующие птицы нашего края
Презентация на тему Ознакомление с окружающим миром: зимующие птицы нашего края  ЯЗЫК БЛОК - СХЕМ
ЯЗЫК БЛОК - СХЕМ Управление своими деньгами
Управление своими деньгами Тургенев «Бирюк»
Тургенев «Бирюк» Презентация на тему Соседи восточных славян (6 класс)
Презентация на тему Соседи восточных славян (6 класс) Иконки автомобильные
Иконки автомобильные 279789
279789 Электронные проводные звонки
Электронные проводные звонки Структурные модели
Структурные модели Комплекс QUIK – полезный функционал: учет позиций, маржинальная торговля, субброкерское обслуживание, единая денежная позиция, сроч
Комплекс QUIK – полезный функционал: учет позиций, маржинальная торговля, субброкерское обслуживание, единая денежная позиция, сроч Периодизация детства
Периодизация детства