Презентация на тему Многогранники и их различия

В стереометрии изучаются фигуры в пространстве, называемые телами. Наглядно тело надо представлять себе как часть пространства, занятую физическим телом и ограниченную поверхностью.
Многогранник – это такое тело, поверхность которого состоит из конечного числа плоских многоугольников.
Многогранник называется выпуклым, если он расположен по одну сторону плоскости каждого плоского многоугольника на его поверхности. Общая часть такой плоскости и поверхности выпуклого многогранника называется гранью.
Стороны граней называются ребрами многогранника, а вершины – вершинами многогранника.

Поясним сказанное на примере знакомого вам куба.
Куб есть выпуклый многогранник. Его поверхность состоит из шести квадратов.
Они являются его гранями. Ребрами куба являются стороны этих квадратов АВ, ВС, ДЕ… Вершинами куба являются вершины квадратов А, В, С, Д….У куба шесть граней, двенадцать ребер и восемь вершин.

Простейшим многогранникам – призмам и пирамидам, которые будут основным объектом нашего изучения, - мы дадим такие определения, которые не используют понятие тела. Они будут определены как геометрические фигуры с указанием всех принадлежащих им точек пространства.
Далее мы обратим наше внимание на три вида многогранников.
Чтобы перейти к одному из этих видов щелкни мышкой на нужном объекте.

План урока:
Понятие призмы и ее основные элементы
Виды призм
Площадь поверхности призмы
Теорема о площади боковой поверхности
Контрольные вопросы
План урока:
Понятие призмы и ее основные элементы
Виды призм
Площадь поверхности призмы
Теорема о площади боковой поверхности
Контрольные вопросы
Призма

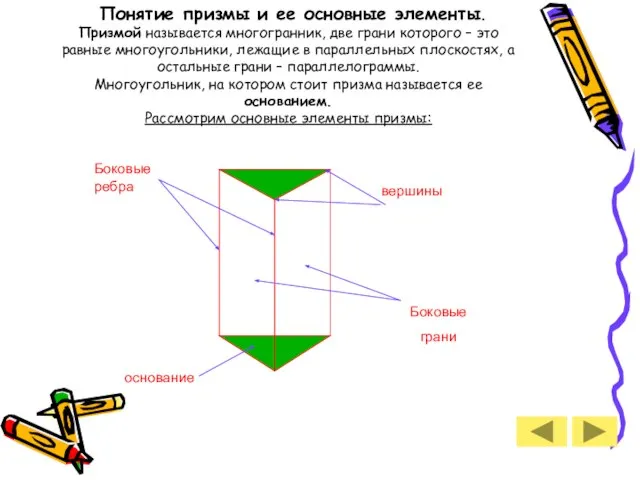
Понятие призмы и ее основные элементы.
Призмой называется многогранник, две грани которого – это равные многоугольники, лежащие в параллельных плоскостях, а остальные грани – параллелограммы.
Многоугольник, на котором стоит призма называется ее основанием.
Рассмотрим основные элементы призмы:
вершины
Боковые
грани
основание
Боковые
ребра

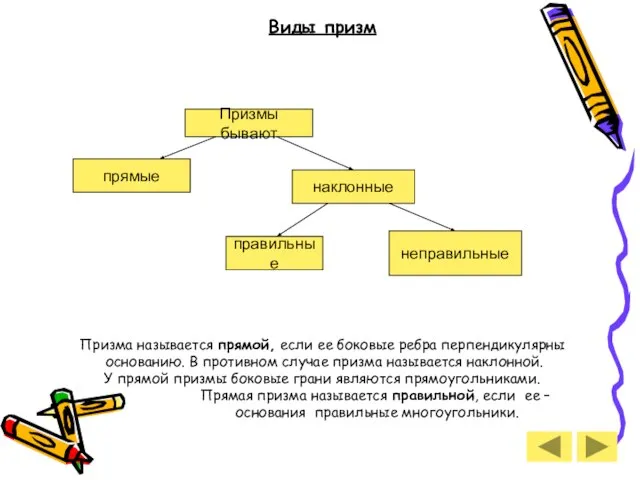
Виды призм
Призма называется прямой, если ее боковые ребра перпендикулярны основанию. В противном случае призма называется наклонной.
У прямой призмы боковые грани являются прямоугольниками.
Прямая призма называется правильной, если ее –
основания правильные многоугольники.

Площадь поверхности призмы
Теорема о площади боковой поверхности призмы
Боковой поверхностью призмы называется сумма площадей ее боковых граней.
Полной поверхностью призмы называется сумма боковой поверхности и площадей оснований.
Теорема. Боковая поверхность прямой призмы равна произведению периметра основания на высоту призмы, то есть на длину бокового ребра.
Доказательство:
Боковые грани призмы - прямоугольники. Основания этих прямоугольников являются сторонами многоугольника, лежащего в основании призмы, а высоты равны длине боковых ребер. Отсюда следует, что боковая поверхность призмы равна:
S=а•Н+в•Н+с•Н=Н•(а+в+с)=Р•Н,
где Р –периметр основания призмы.
Н
а
в
с

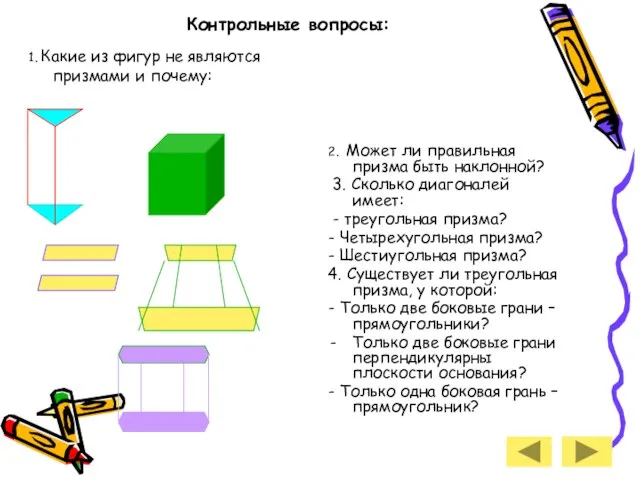
Контрольные вопросы:
1. Какие из фигур не являются призмами и почему:
2. Может ли правильная призма быть наклонной?
3. Сколько диагоналей имеет:
- треугольная призма?
- Четырехугольная призма?
- Шестиугольная призма?
4. Существует ли треугольная призма, у которой:
- Только две боковые грани – прямоугольники?
Только две боковые грани перпендикулярны плоскости основания?
- Только одна боковая грань – прямоугольник?

Урок 3-4
План урока:
Понятие параллелепипеда, его виды и элементы
Свойства параллелепипеда
Виды параллелепипедов
Контрольные вопросы
Параллелепипед

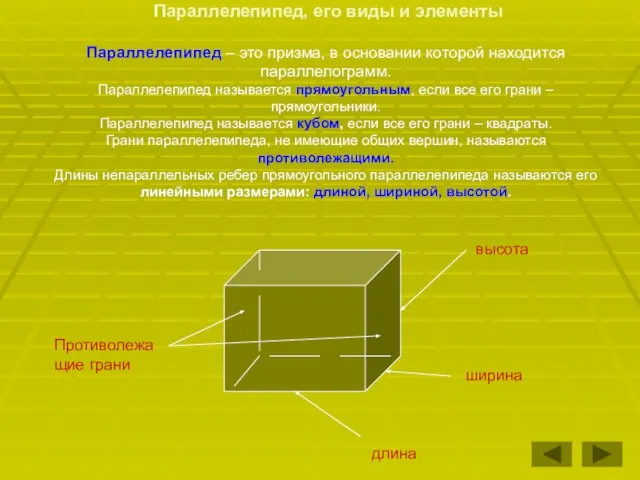
Параллелепипед, его виды и элементы
Параллелепипед – это призма, в основании которой находится параллелограмм.
Параллелепипед называется прямоугольным, если все его грани – прямоугольники.
Параллелепипед называется кубом, если все его грани – квадраты.
Грани параллелепипеда, не имеющие общих вершин, называются противолежащими.
Длины непараллельных ребер прямоугольного параллелепипеда называются его линейными размерами: длиной, шириной, высотой.
высота
ширина
длина
Противолежащие грани

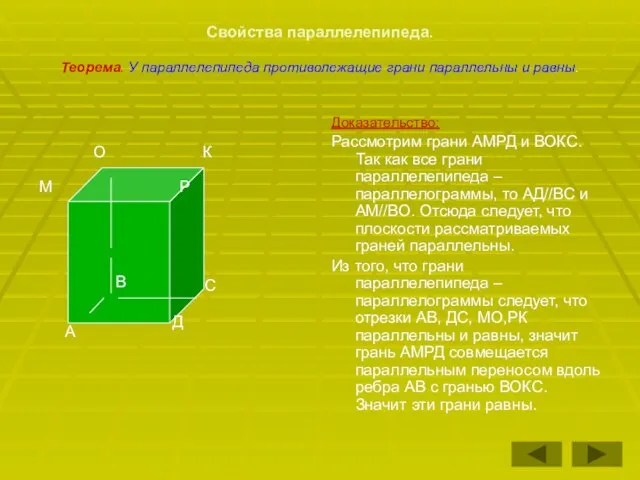
Свойства параллелепипеда.
Теорема. У параллелепипеда противолежащие грани параллельны и равны.
Доказательство:
Рассмотрим грани АМРД и ВОКС. Так как все грани параллелепипеда – параллелограммы, то АД//ВС и АМ//ВО. Отсюда следует, что плоскости рассматриваемых граней параллельны.
Из того, что грани параллелепипеда –параллелограммы следует, что отрезки АВ, ДС, МО,РК параллельны и равны, значит грань АМРД совмещается параллельным переносом вдоль ребра АВ с гранью ВОКС. Значит эти грани равны.

Свойства параллелепипеда.
Теорема. У параллелепипеда диагонали пересекаются в одной точке и точкой пересечения делятся пополам.
Доказательство:
Рассмотрим диагонали ДО и СМ. Так как АВОМ и АВСД – параллелограммы с общей стороной АВ, то МО//ДС и они лежат в одной плоскости. Эта плоскость пересекает противолежащие грани АДРМ и ВСКО па параллельным прямым МД и ОС. Значит МДОС – параллелограмм, и МС и ОД – его диагонали. Поэтому они пересекаются и точкой пересечения делятся пополам.

Свойства параллелепипеда.
Теорема. В прямоугольном параллелепипеде квадрат любой его диагонали равен сумме квадратов трех его измерений..
Доказательство:
Рассмотрим прямоугольный параллелепипед АВСДМРКО.
Из прямоугольного треугольника АДС по теореме Пифагора:
АС2=АД2+ДС2 .
Из прямоугольного треугольника АСК по теореме Пифагора:
АК2=АС2+СК2. Отсюда:
АК2=АД2+ДС2+СК2

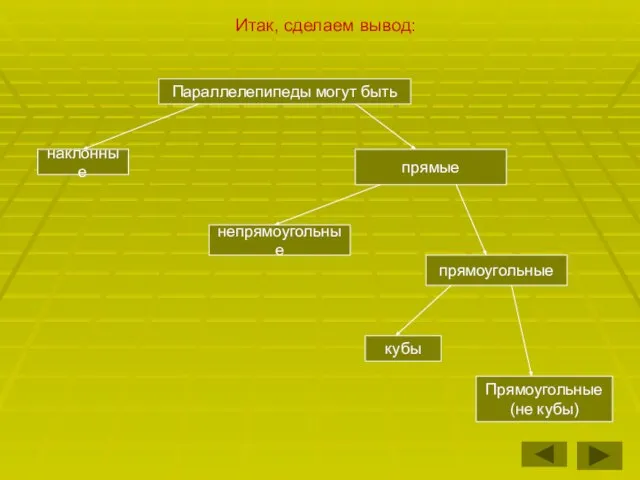
Итак, сделаем вывод:
Параллелепипеды могут быть
прямые
прямоугольные
наклонные
непрямоугольные
кубы
Прямоугольные
(не кубы)

А теперь ответьте на
Контрольные вопросы:
Верно ли утверждение:
- все грани прямоугольного параллелепипеда – прямоугольники;
- все грани прямого параллелепипеда – прямоугольники;
- ни одна грань наклонного параллелепипеда не является прямоугольником;
- прямоугольный параллелепипед есть правильная призма.
Может ли боковая грань наклонного параллелепипеда быть прямоугольником?
Сколько боковых граней наклонного параллелепипеда могут быть прямоугольниками?
Существует ли параллелепипед, у которого
- только одна боковая грань перпендикулярна основанию?
- только одна грань – прямоугольник?
- четыре грани –прямоугольники?
Верно ли утверждение: длины всех диагоналей прямоугольного параллелепипеда равны? Сформулируйте утверждение, обратное данному. Справедливо ли оно?
Справедливо ли утверждение: в наклонном параллелепипеде не может быть ни одной пары равных диагоналей?

Урок 5-6
План урока:
Понятие пирамиды и ее основные элементы.
Площадь поверхности пирамиды.
Теорема о площади боковой поверхности пирамиды.
Усеченная пирамида и ее элементы.
Контрольные вопросы.
Пирамида и усеченная пирамида

Понятие пирамиды и ее основные элементы
Пирамидой называется многогранник, в основании которого находится многоугольник, а остальные грани – это треугольники, сходящиеся в одной вершине.
Высотой пирамиды называется перпендикуляр, опущенный из ее вершины на плоскость основания.
Пирамида называется правильной, если в ее основании находится правильный многоугольник, а высота пирамиды падает в его центр. Высота боковой грани правильной пирамиды называется апофемой.
Рассмотрим элементы пирамиды на чертеже:
Боковые
ребра
вершина
высота
апофема
основание

Площадь поверхности пирамиды.
Теорема о площади боковой поверхности правильной пирамиды.
Боковой поверхностью пирамиды называется сумма площадей ее боковых граней.
Теорема. Площадь боковой поверхности правильной пирамиды равна произведению полупериметра основания на апофему.
Доказательство:
Боковые грани пирамиды – треугольники, а площадь треугольника равна половине произведения основания на высоту.
Значит площадь боковой поверхности равна:
S=1/2a•h+1/2a•h+1/2a•h=1/2h•(a+a+a)=
=1/2P•h,
Где Р – периметр основания пирамиды.
а
а
а
h

Усеченная пирамида и ее элементы.
Усеченной называется пирамида, полученная из обычной пирамиды путем отсечения ее вершины плоскостью, параллельной основанию.
Высотой усеченной пирамиды называется отрезок, соединяющий ее основания и перпендикулярный им обоим.
Усеченная пирамида называется правильной, если в ее основаниях находятся правильные многоугольники.
Высота боковой грани правильной усеченной пирамиды называется апофемой.
Рассмотрим элементы усеченной пирамиды на чертеже:
апофема
высота
основания