Слайд 2 1). Определение
2). Виды
3). Свойства числовых неравенств
4).

Основные свойства неравенств
4). Типы
5). Способы решения
Слайд 3
Запись вида
а>в или а<в
называется неравенством.

Слайд 4
Неравенства вида а≥в, а≤в называется ……
Неравенства вида а>в, а<в называется……

Слайд 51). Если а>в, то в<а.
2).Если а>в, в>с, то а>с.
3). Если а>в, с-любое

число, то а+с>в+с.
4). Если а>в, с>х, то а+с>в+х.
5). Если а>в, с>0, то ас>вс.
6). Если а>в, с<0, то ас<вс.
7). Если а>о, с>0,то > .
8). Если а>о, с>0, а>с, то >
Слайд 61). Любой член неравенства можно переносить из одной части неравенства в другую,

изменив его знак на противоположный, при этом знак неравенства не меняется.
Слайд 72).Обе части неравенства можно умножить или разделить на одно и тоже положительное

число, при этом знак неравенства не изменится. Если это число отрицательное, то знак неравенства изменится на противоположное.
Слайд 8ЛИНЕЙНЫЕ
КВАДРАТНЫЕ
РАЦИОНАЛЬНЫЕ
ИРРАЦИОНАЛЬНЫЕ
НЕРАВЕНСТВА
Слайд 9I).I).Линейное неравенство.
1). х+4<0; 2).2х+4≥6;
х<-4; 2х≥-2;
-4 х х≥-1;
Ответ: (-∞;-4).
-1

х
Ответ: [-1;+∞).
Слайд 101.Решить неравенства.
1). х+2≥2,5х-1;
2).х- 0,25(х+4)+0,5(3х-1)>3;
3).
4).х²+х<х(х-5)+2;
5).

Слайд 112.
Найдите наименьшие целые числа, являющиеся решениями неравенств
1.2(х-3)-1-3(х-2)-4(х+1)>0;
2.0,2(2х+2)-0,5(х-1)<2.
3.
Найдите наименьшие натуральные числа, являющиеся решениями

неравенства
3х-3<1,5х+4.
Слайд 12II).Квадратные неравенства.
Способы решения:
Графический
С применением
систем
неравенств
Метод
интервалов
Слайд 131.1).Метод интервалов
(для решения квадратного уравнения)
ах²+вх+с>0
1). Разложим данный многочлен на множители, т.е.

представим в виде
а(х- )(х- )>0.
2).корни многочлена нанести на числовую ось;
3). Определить знаки функции в каждом из промежутков;
4). Выбрать подходящие интервалы и записать ответ.
Слайд 14x²+x-6=0; (х-2)(х+3)=0;
Ответ: (-∞;-3)v(2;+∞).
х
+
2
-3
+
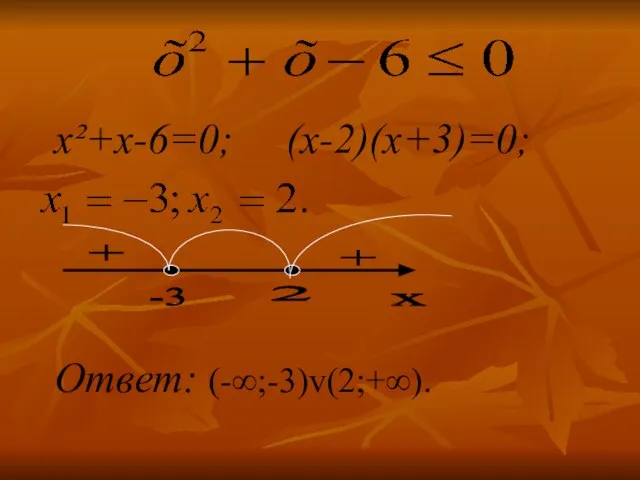
Слайд 151.Решение неравенства методом интервалов.
1). х(х+7)≥0;
2).(х-1)(х+2)≤0;
3).х-х²+2<0;
4).-х²-5х+6>0;
5).х(х+2)<15.

Слайд 16Домашняя работа:
Сборник 1).стр. 109 № 128-131
Сборник 2).стр.111 №3.8-3.10; 3.22;3.37-3.4

Слайд 171.2).Решение квадратных неравенств графически
1). Определить направление ветвей параболы, по знаку первого коэффициента

квадратичной функции.
2).Найти корни соответствующего квадратного уравнения;
3).Построить эскиз графика и по нему определить промежутки, на которых квадратичная функция принимает положительные или отрицательные значения.
Слайд 18Пример:
х²+5х-6≤0
y= х²+5х-6 (квадратичная функция, график парабола, а=1, ветви направлены вверх)
х²+5х-6=0; корни этого

уравнения: 1 и -6.
у
+ +
-6 1 x
Ответ: [-6;1].
-
Слайд 19Решите графически неравенства:
1).х²-3х<0;
2).х²-4х>0;
3).х²+2х≥0;
4). -2х²+х+1≤0;
(0;3)
(-∞;0)U(4;+∞)
(-∞;-2]U[0;+∞)
(-∞;-0,5]U[1;+∞)
![Решите графически неравенства: 1).х²-3х 2).х²-4х>0; 3).х²+2х≥0; 4). -2х²+х+1≤0; (0;3) (-∞;0)U(4;+∞) (-∞;-2]U[0;+∞) (-∞;-0,5]U[1;+∞)](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/278279/slide-18.jpg)
Слайд 20Домашнее задание:
Сборник 1).стр. 115 №176-179.
работы №47,45,42,17,12
(задание №5)
Сборник 2).стр.

116 № 4.4,4.5, 4.11.
работы №6, задание 13.
Слайд 21III).Рациональные неравенства вида
решают методом интервалов.
1) Раскладывают на линейные множители числитель P(x) и

знаменатель Q(x). Если это удается, то дальше поступают так.
2) На числовую ось наносят корни всех линейных множителей. На каждом из промежутков, на которые эти точки разбивают ось, дробь P(x)/ Q(x). сохраняет знак
3) Определяют знак дроби на каждом промежутке.
4) Записывают ответ.
Слайд 22Сборник 1).стр. 109 №132
Сборник 2). Стр. 112-113 № 3.20, 3.21,
3.39-3.42

Слайд 241). Содержащие линейные неравенства.
2). Содержащие квадратное(рациональное) неравенство и линейное неравенство.
3). Содержащие квадратные

неравенства.
4). Двойное неравенство, которое решается с помощью систем.
5). Неравенства с модулем
Слайд 251). 5х+1>6 5x>5 x>1
2x-4<3 ; 2x<7 ; x<3,5.
1 3,5 x
Ответ:

(1;3,5).
Задания:
Сборник 1). Стр. 111№139-142
стр. 170-172 № 711-766
Сборник 2).стр. 110 № 3.4-3.7
Слайд 262). х²-1>0 (x-1)(x+1)>0
x+4<0; x<-4;
+ - +
-4 -1 1 x
Ответ:

(-∞;-4).
Задания:
Сборник 1).стр. 111 № 143-145
Сборник 2). Стр. 112-113 №3.24, 3.25
Слайд 273). х²-4>0
x²-3x+5<0.
Решаем каждое квадратное неравенство в отдельности. Изображаем решения

на числовой прямой и смотрим пересечения этих решений. Записываем ответ.
Задания:
Сборник 1). Стр. 111 № 146-147
Сборник 2).стр. 113, 115 № 3.27, 3.29,
3.47, 3.48
Слайд 284). -12 x-1<1 x<2 Ответ: (-11;2).
x-1>-12; x>-11.
Задания:
Сборник 1).стр. 109

№ 126-127, 134,
стр. 172 №783-790
Сборник 2). Стр. 111 №3.9
Слайд 29
5).| 3х-2|<10
3x-2>-10 x>
3x-2<10; x<4.
Ответ: ( ;4).













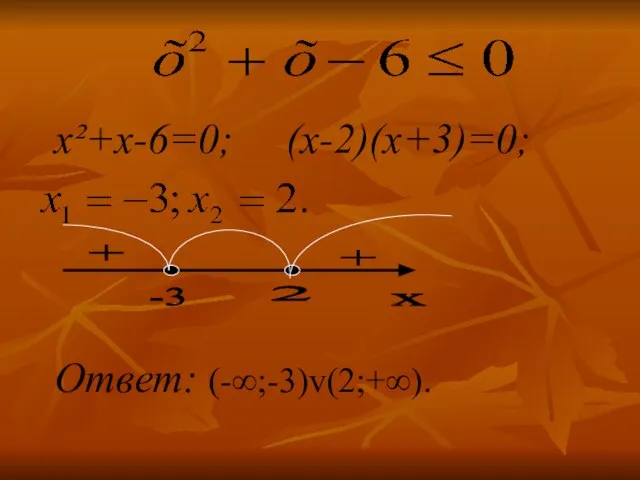




![Решите графически неравенства: 1).х²-3х 2).х²-4х>0; 3).х²+2х≥0; 4). -2х²+х+1≤0; (0;3) (-∞;0)U(4;+∞) (-∞;-2]U[0;+∞) (-∞;-0,5]U[1;+∞)](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/278279/slide-18.jpg)










 Секция «Проектирование учебного плана и программ дисциплин в области начального образования
Секция «Проектирование учебного плана и программ дисциплин в области начального образования Июль 2007
Июль 2007 Район Отрадное. Слайды
Район Отрадное. Слайды Презентация на тему Природные источники углеводородов
Презентация на тему Природные источники углеводородов  Бюджет семьи
Бюджет семьи Презентация на тему: Подходы, методы и инструментарий формирования готовности к самостоятельному определению профессиональных п
Презентация на тему: Подходы, методы и инструментарий формирования готовности к самостоятельному определению профессиональных п Мой друг, отчизне посвятимДуши прекрасные порывы! А.С. Пушкин
Мой друг, отчизне посвятимДуши прекрасные порывы! А.С. Пушкин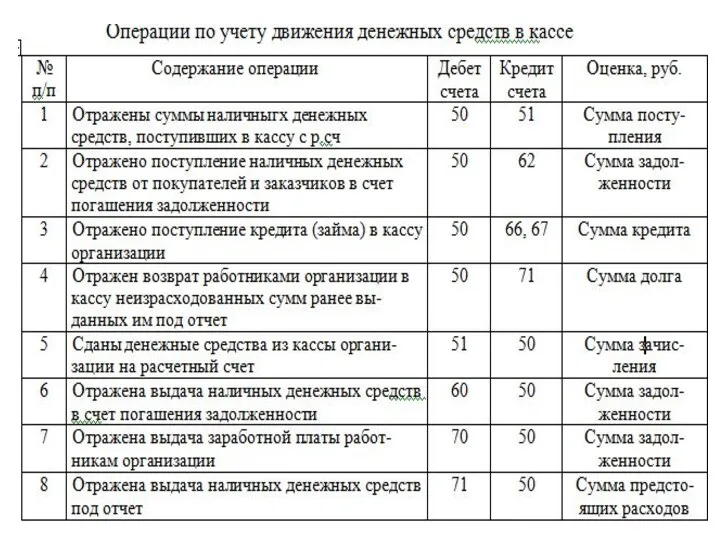 Операции по учету движения денежных средств в кассе
Операции по учету движения денежных средств в кассе Вниманию субъектов предпринимательства!
Вниманию субъектов предпринимательства! Перспективы развития информационных технологий в библиотечной сфере Хабаровского края
Перспективы развития информационных технологий в библиотечной сфере Хабаровского края Совещание с ответственными за планирование и результаты инновационной деятельности в образовательных учреждениях ЮЗАО
Совещание с ответственными за планирование и результаты инновационной деятельности в образовательных учреждениях ЮЗАО Презентация на тему история Крымской войны
Презентация на тему история Крымской войны  Искусство общения
Искусство общения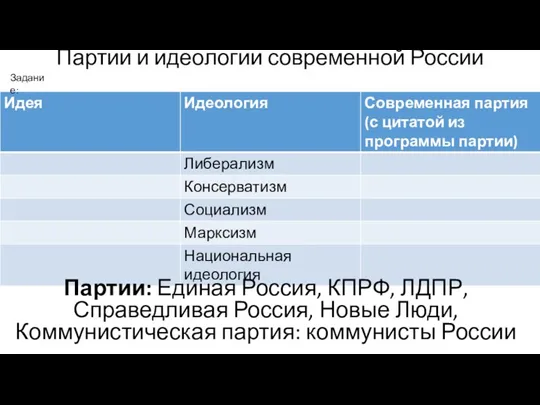 Партии и идеологии современной России
Партии и идеологии современной России STRATEGIC VISION AND 2007/08 ACADEMIC YEAR Марина ЛАТУХА Старший преподаватель кафедры организационного поведения и управления персоналом Высшая шк
STRATEGIC VISION AND 2007/08 ACADEMIC YEAR Марина ЛАТУХА Старший преподаватель кафедры организационного поведения и управления персоналом Высшая шк Дата открытия музея – 01.09.1983 год. Музей создавался по инициативе ветеранов II механизированного корпуса, при поддержке директора Г
Дата открытия музея – 01.09.1983 год. Музей создавался по инициативе ветеранов II механизированного корпуса, при поддержке директора Г Симметрия в цветочном мире
Симметрия в цветочном мире Виды изобразительного искусства
Виды изобразительного искусства Дания
Дания Творчество Б. Акунина
Творчество Б. Акунина Презентация на тему Домашние животные. Кто где живет?
Презентация на тему Домашние животные. Кто где живет?  Философско-методологические проблемы естествознания
Философско-методологические проблемы естествознания Разминка: определите вид химической связи HNO 3 Cl 2 KHSO 4 H2O H2O NaOH CaO Cu.
Разминка: определите вид химической связи HNO 3 Cl 2 KHSO 4 H2O H2O NaOH CaO Cu. «В Петербурге жила когда-то очаровательная женщина. Такая очаровательная, что я не знаю ни одного живого существа, не отдавшего ей
«В Петербурге жила когда-то очаровательная женщина. Такая очаровательная, что я не знаю ни одного живого существа, не отдавшего ей  我的朋友去外国旅游
我的朋友去外国旅游 Вы планируете провести масштабное конгрессное мероприятие (коллегию, конференцию, «круглый стол», семинар и т.п.) с приглашением ру
Вы планируете провести масштабное конгрессное мероприятие (коллегию, конференцию, «круглый стол», семинар и т.п.) с приглашением ру Презентация на тему Преобразование энергии в колебательном контуре
Презентация на тему Преобразование энергии в колебательном контуре  Ученическая научная конференция юных филологов «Дебют - 2011»
Ученическая научная конференция юных филологов «Дебют - 2011»