Презентация на тему Параллельность

Параллельные прямые

Определение.
Две прямые называются параллельными, если они не пересекаются.
а
b
аIIb

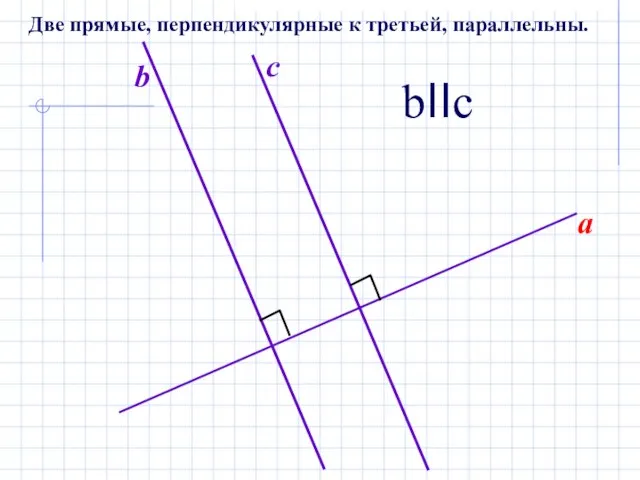
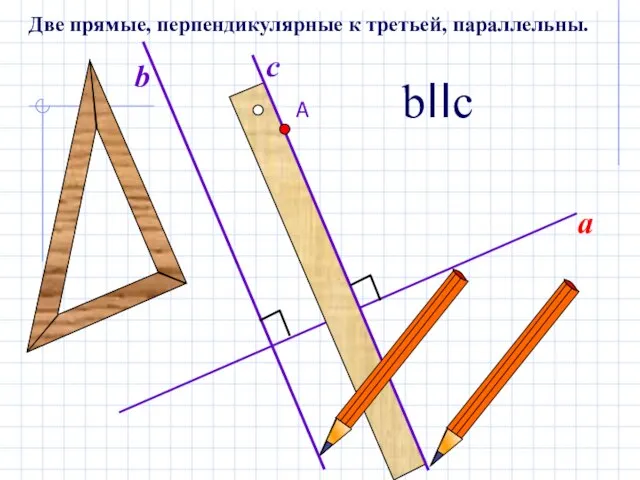
a
b
c
bIIc
Две прямые, перпендикулярные к третьей, параллельны.

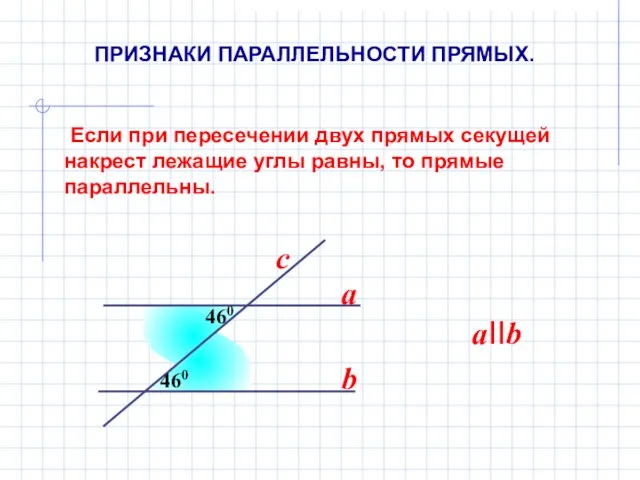
Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
460
460
a
b
aIIb
c
ПРИЗНАКИ ПАРАЛЛЕЛЬНОСТИ ПРЯМЫХ.

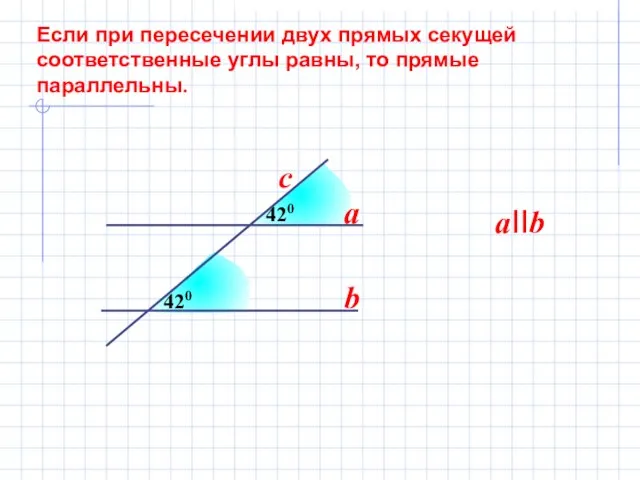
420
Если при пересечении двух прямых секущей
соответственные углы равны, то прямые
параллельны.
420
a
b
aIIb
c

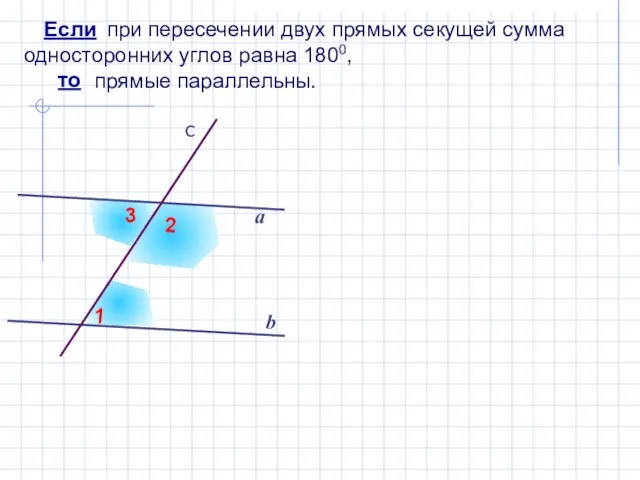
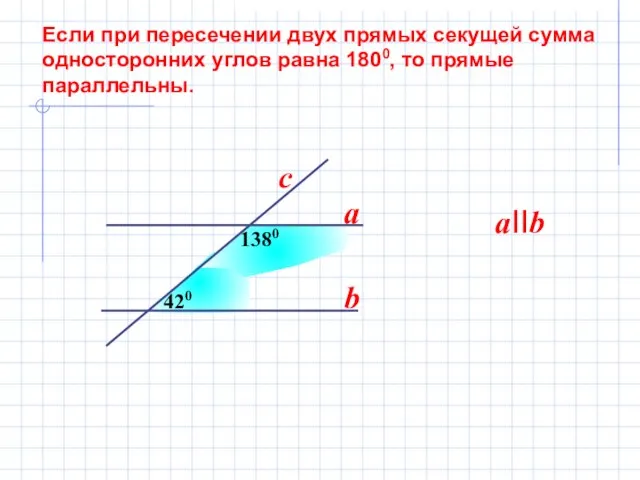
при пересечении двух прямых секущей сумма односторонних углов равна 1800, прямые параллельны.
b
а
Если
то
1
2
c

Если при пересечении двух прямых секущей сумма
односторонних углов равна 1800, то прямые
параллельны.
420
1380
a
b
aIIb
c

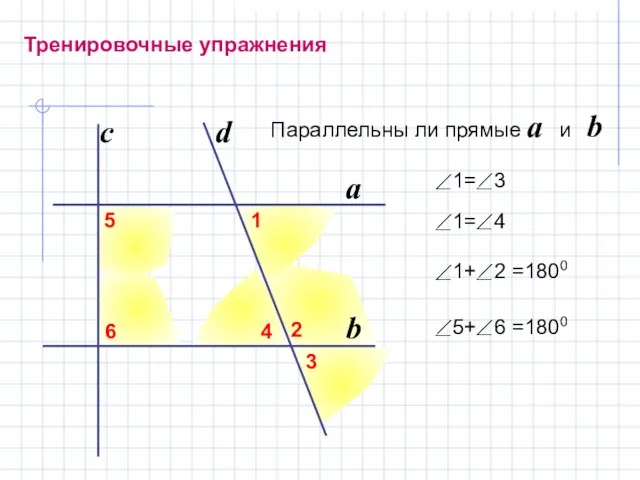
Тренировочные упражнения
Параллельны ли прямые a и b
b
a
d
c
1
3
2
4
6
5

А
a
b
c
bIIc
Две прямые, перпендикулярные к третьей, параллельны.

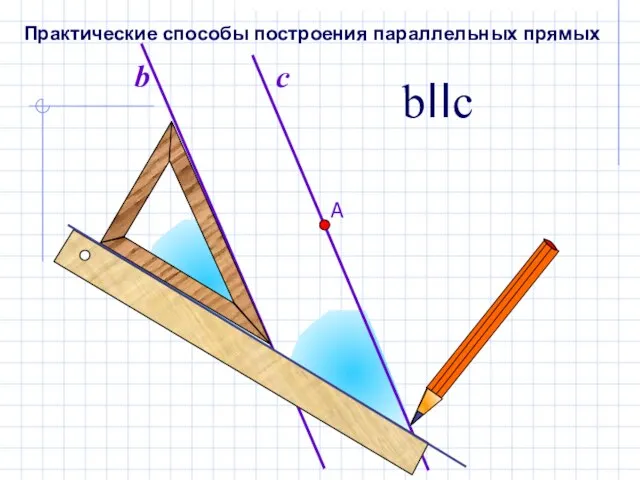
b
bIIc
Практические способы построения параллельных прямых

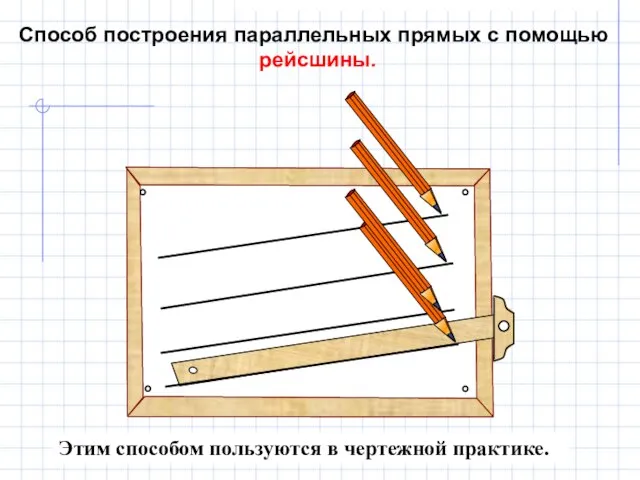
Этим способом пользуются в чертежной практике.
Способ построения параллельных прямых с помощью
рейсшины.

Параллельность прямой с плоскостью

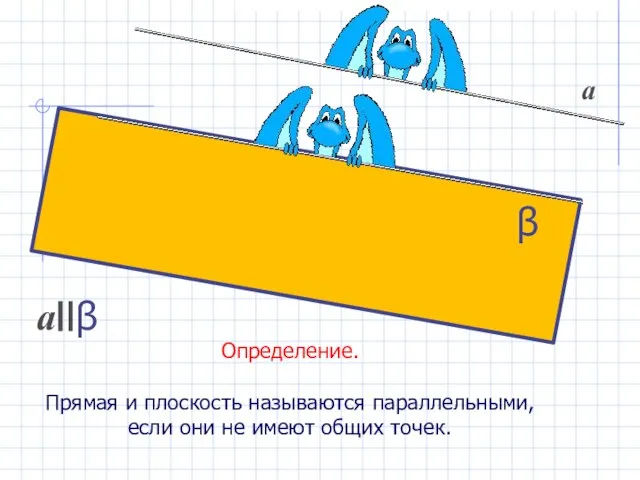
Определение.
Прямая и плоскость называются параллельными, если они не имеют общих точек.
аIIβ
а
β

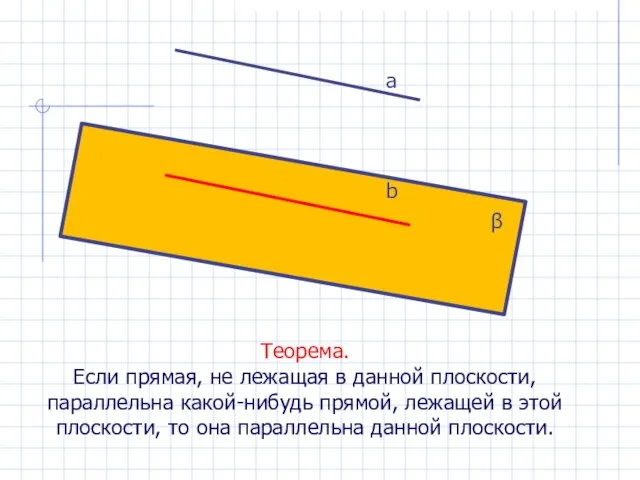
Теорема.
Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.
a
b
β

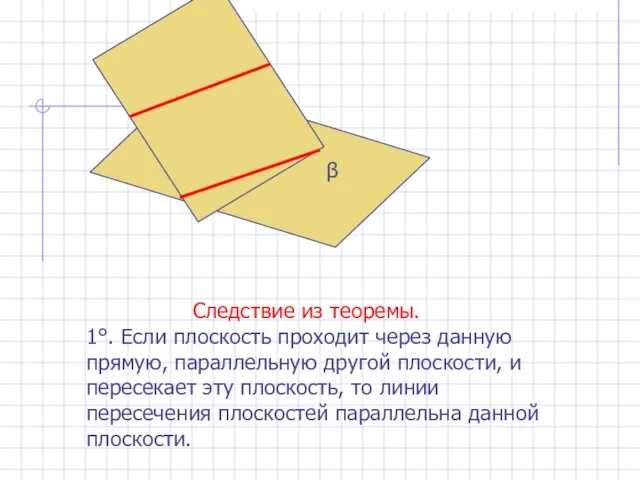
Следствие из теоремы.
1°. Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линии пересечения плоскостей параллельна данной плоскости.
β

Следствие из теоремы.
2°. Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости.

Параллельность плоскостей

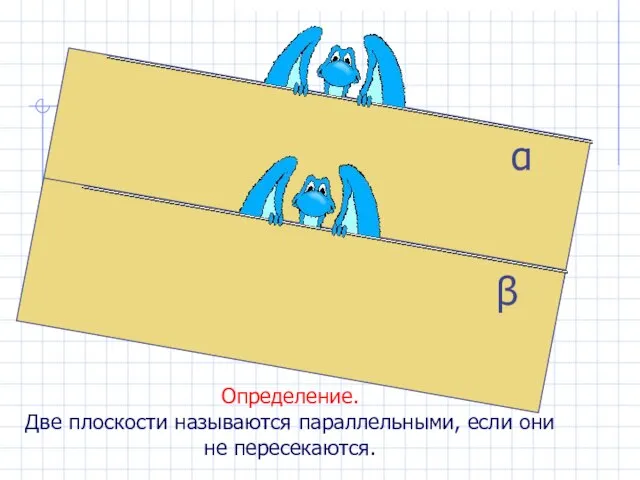
β
α
Определение.
Две плоскости называются параллельными, если они не пересекаются.

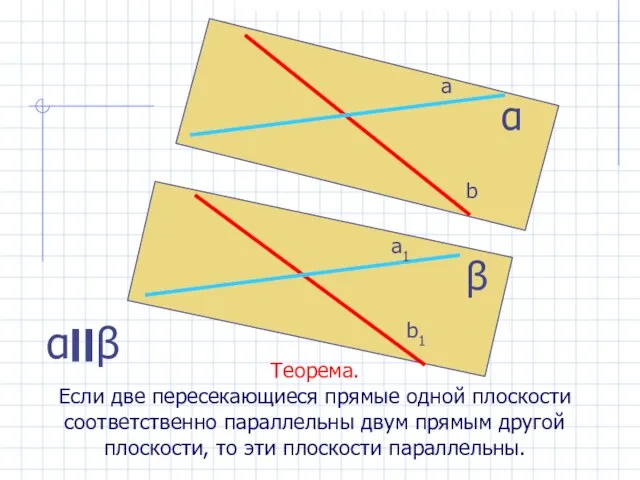
Теорема.
Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.
α
β
a
b
a1
b1
α׀׀β

Свойства параллельных плоскостей

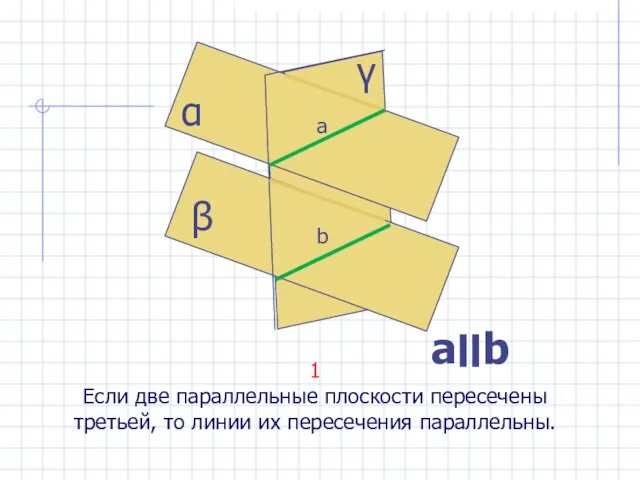
1
Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.
α
β
γ
a
b
a׀׀b