Презентация на тему Призма

Определение 1.
Многогранник, две грани которого - одноименные многоугольники, лежащие в параллельных плоскостях, а любые два ребра, не лежащие в этих плоскостях, параллельны, называется призмой.
Термин “призма” греческого происхождения и буквально означает “отпиленное” (тело).
Многоугольники, лежащие в параллельных плоскостях, называют основаниями призмы, а остальные грани - боковыми гранями.
Поверхность призмы, таким образом, состоит из двух равных многоугольников (оснований) и параллелограммов (боковых граней). Различают призмы треугольные, четырехугольные, пятиугольные и т.д. в зависимости от числа вершин основания.

Все призмы делятся на прямые и наклонные.
(рис. 2)
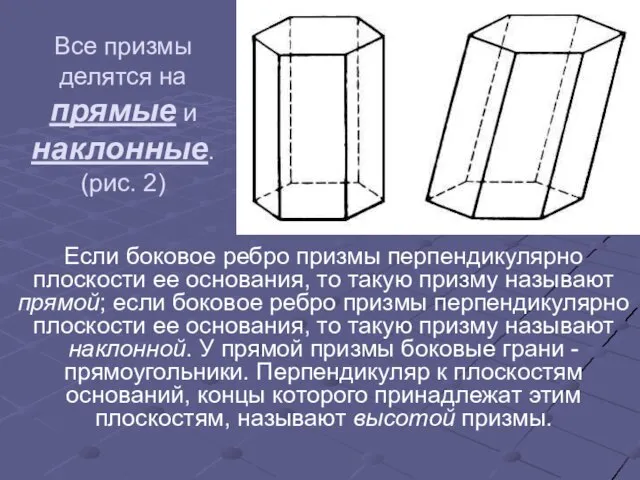
Если боковое ребро призмы перпендикулярно плоскости ее основания, то такую призму называют прямой; если боковое ребро призмы перпендикулярно плоскости ее основания, то такую призму называют наклонной. У прямой призмы боковые грани - прямоугольники. Перпендикуляр к плоскостям оснований, концы которого принадлежат этим плоскостям, называют высотой призмы.

Свойства призмы.
1о. Основания призмы являются равными многоугольниками.
2о. Боковые грани призмы являются параллелограммами.
3о. Боковые ребра призмы равны.

Площадь поверхности призмы и площадь боковой поверхности призмы.
Поверхность многогранника состоит из конечного числа многоугольников (граней). Площадь поверхности многогранника есть сумма площадей всех его граней. Площадь поверхности призм (Sпр) равна сумме площадей ее боковых граней (площади боковой поверхности Sбок) и площадей двух оснований (2Sосн) - равных многоугольников: Sпов=Sбок+2Sосн.
Теорема. Площадь боковой поверхности призмы равна произведению периметра ее перпендикулярного сечения и длины бокового ребра.

Доказательство.
Боковые грани прямой призмы - прямоугольники, основания которых-стороны основания призмы, а высоты равны высоте h призмы. Sбок поверхности призмы равна сумме S указанных треугольников, т.е. равна сумме произведений сторон основания на высоту h. Вынося множитель h за скобки, получим в скобках сумму сторон основания призмы, т.е. периметр P. Итак, Sбок =Ph. Теорема доказана.
Следствие. Площадь боковой поверхности прямой призмы равна произведению периметра ее основания и высоты.
Действительно, у прямой призмы основание можно рассматривать как перпендикулярное сечение, а боковое ребро есть высота.

Сечение призмы
1. Сечение призмы плоскостью, параллельной основанию. В сечении образуется многоугольник, равный многоугольнику, лежащему в основании.
2. Сечение призмы плоскостью, проходящей через два не соседних боковых ребра. В сечении образуется параллелограмм. Такое сечение называется диагональным сечением призмы. В некоторых случаях может получаться ромб, прямоугольник или квадрат.

Сечение ПРИЗМЫ.

Определение 2.
Прямая призма, основанием которой служит правильный многоугольник, называется правильной призмой. Свойства правильной призмы
1о. Основания правильной призмы являются правильными многоугольниками.
2о. Боковые грани правильной призмы являются равными прямоугольниками.
3о. Боковые ребра правильной призмы равны.

Сечение правильной призмы.
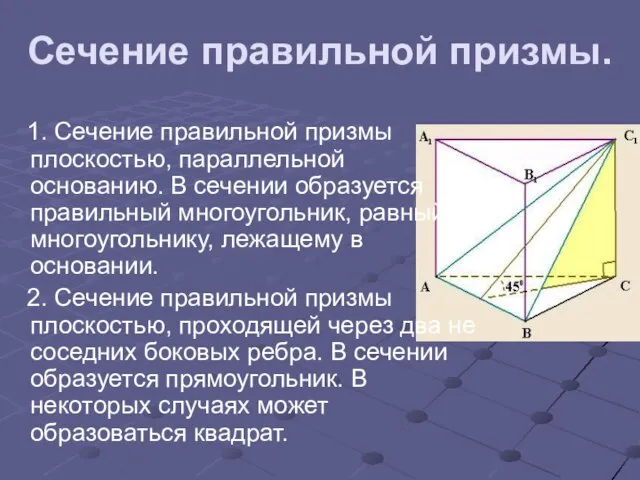
1. Сечение правильной призмы плоскостью, параллельной основанию. В сечении образуется правильный многоугольник, равный многоугольнику, лежащему в основании.
2. Сечение правильной призмы плоскостью, проходящей через два не соседних боковых ребра. В сечении образуется прямоугольник. В некоторых случаях может образоваться квадрат.

Симметрия правильной призмы
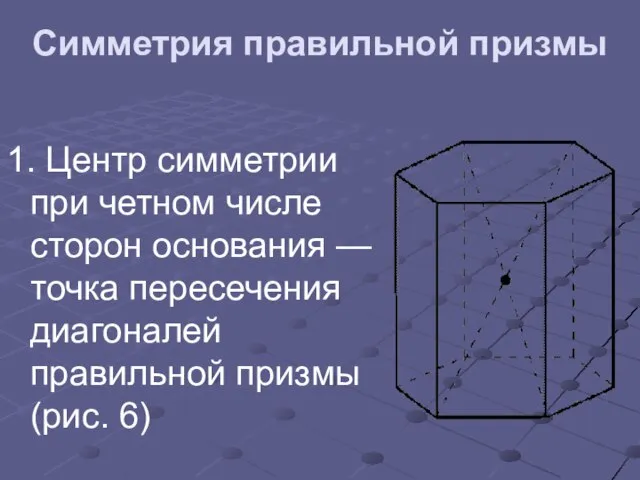
1. Центр симметрии при четном числе сторон основания — точка пересечения диагоналей правильной призмы (рис. 6)

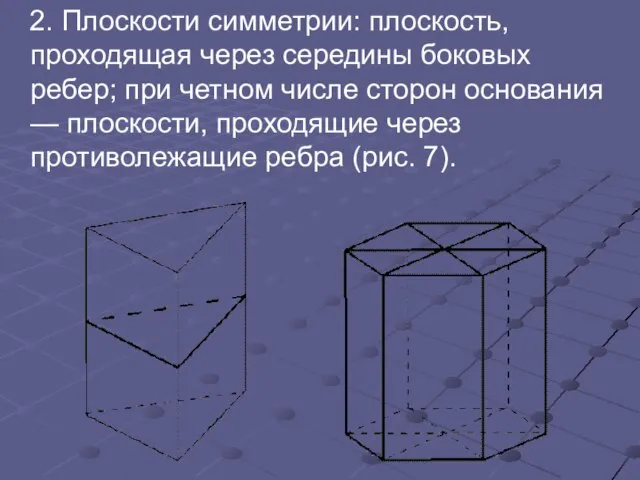
2. Плоскости симметрии: плоскость, проходящая через середины боковых ребер; при четном числе сторон основания — плоскости, проходящие через противолежащие ребра (рис. 7).

3. Оси симметрии: при четном числе сторон основания — ось симметрии, проходящая через центры оснований, и оси симметрии, проходящие через точки пересечения диагоналей противолежащих боковых граней (рис. 8).