Презентация на тему Призма и ее свойства

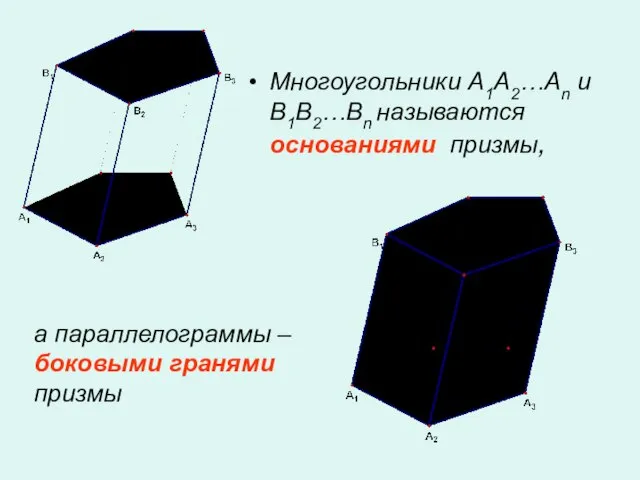
Многоугольники A1A2…An и B1B2…Bn называются основаниями призмы,
а параллелограммы – боковыми гранями призмы

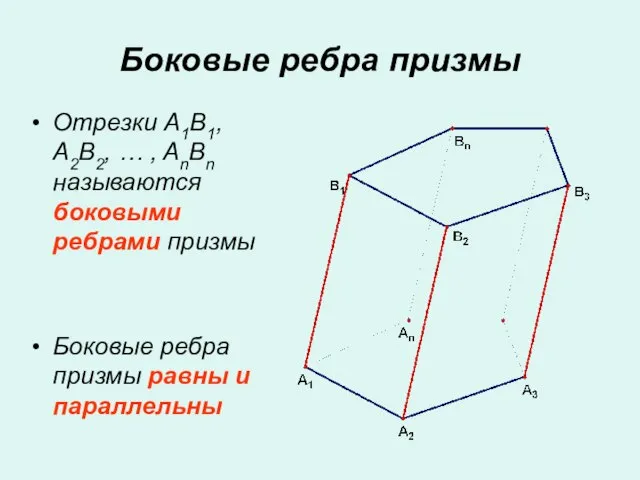
Отрезки A1B1, A2B2, … , AnBn называются боковыми ребрами призмы
Боковые ребра призмы равны и параллельны
Боковые ребра призмы

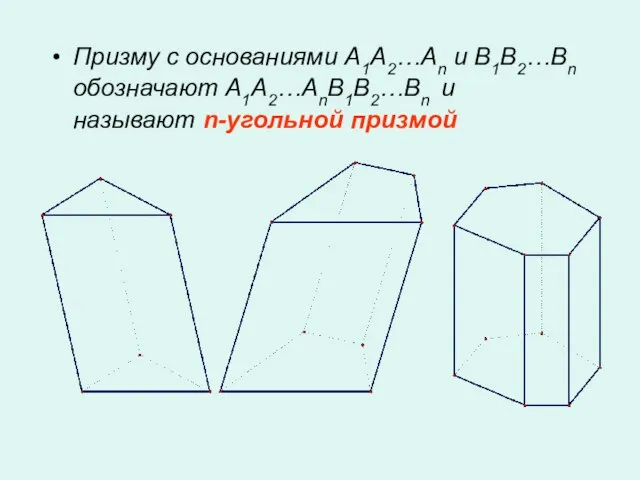
Призму с основаниями A1A2…An и B1B2…Bn обозначают A1A2…AnB1B2…Bn и называют n-угольной призмой

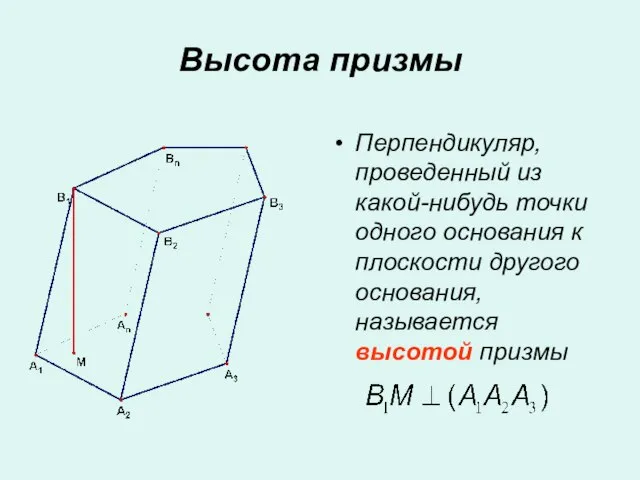
Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы
Высота призмы

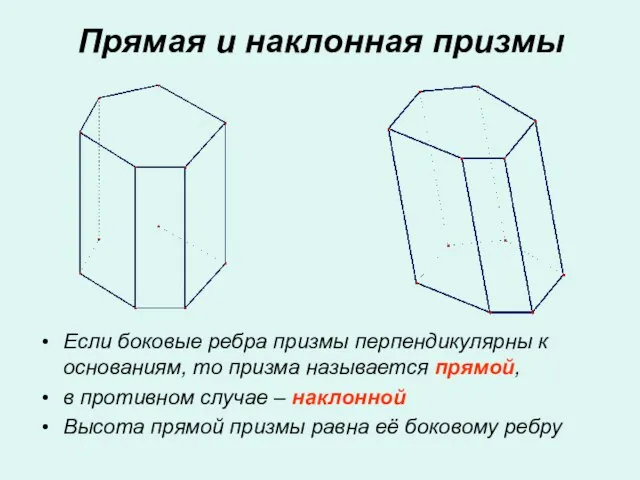
Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой,
в противном случае – наклонной
Высота прямой призмы равна её боковому ребру
Прямая и наклонная призмы

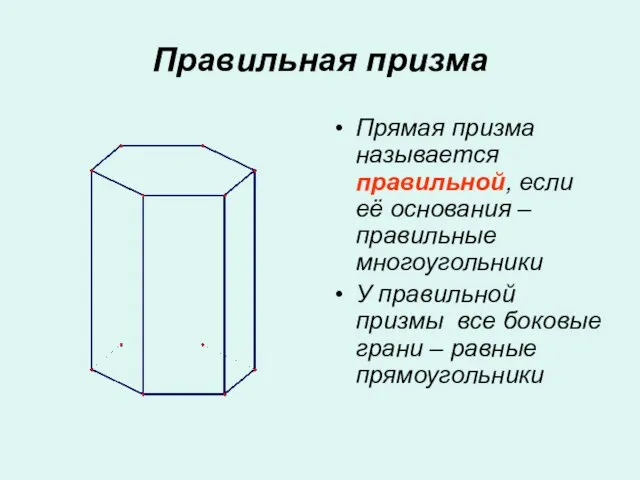
Правильная призма
Прямая призма называется правильной, если её основания – правильные многоугольники
У правильной призмы все боковые грани – равные прямоугольники

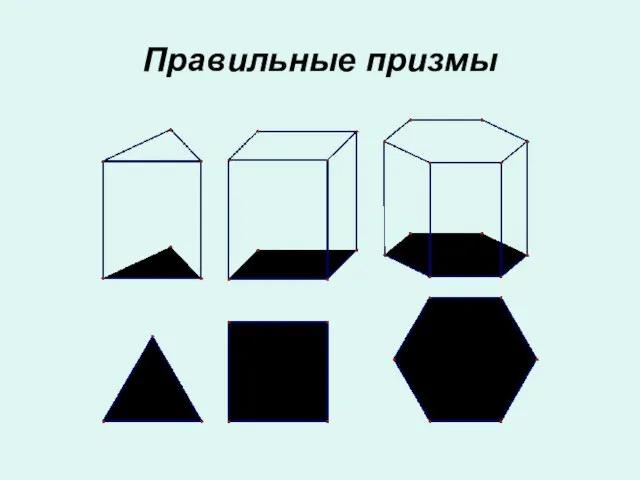
Правильные призмы

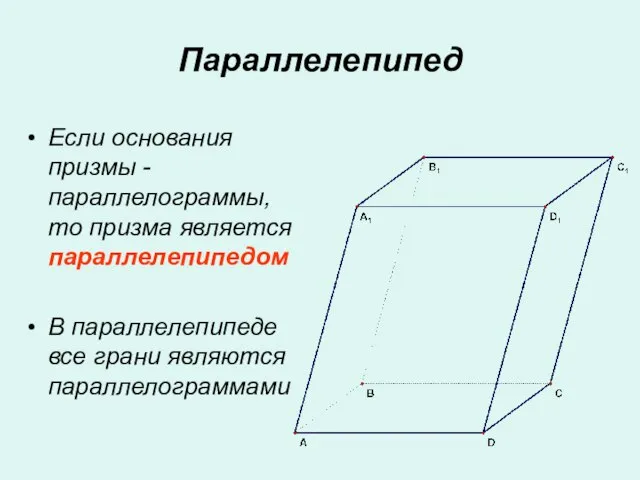
Параллелепипед
Если основания призмы - параллелограммы, то призма является параллелепипедом
В параллелепипеде все грани являются параллелограммами

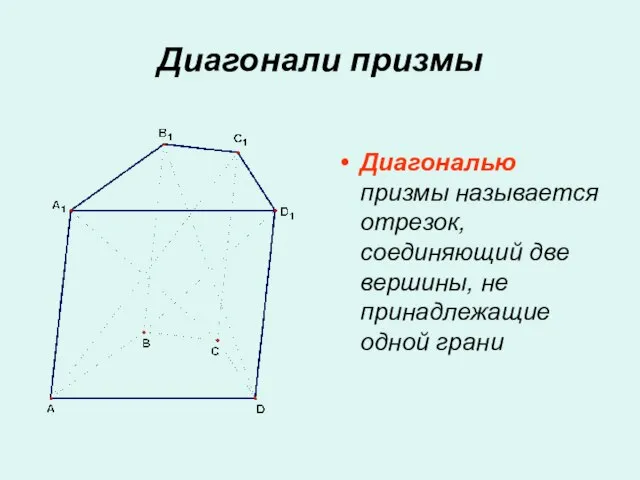
Диагонали призмы
Диагональю призмы называется отрезок, соединяющий две вершины, не принадлежащие одной грани

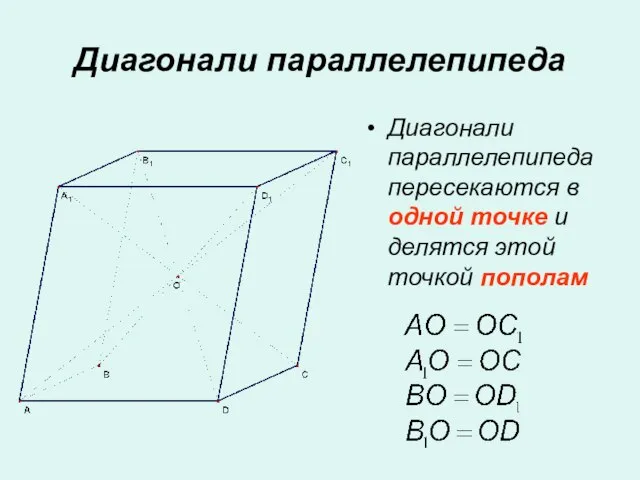
Диагонали параллелепипеда
Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам

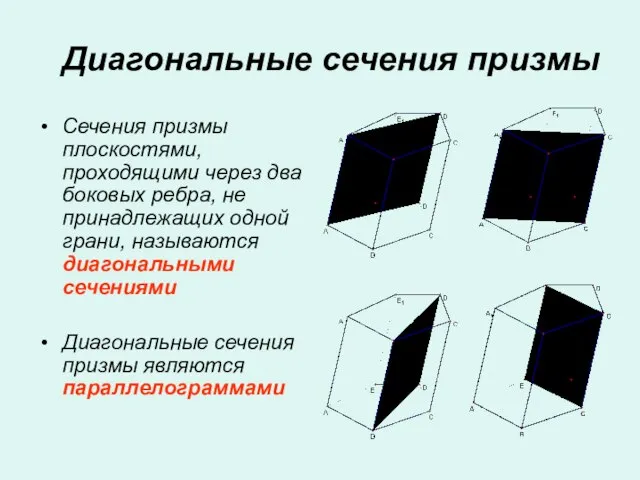
Диагональные сечения призмы
Сечения призмы плоскостями, проходящими через два боковых ребра, не принадлежащих одной грани, называются диагональными сечениями
Диагональные сечения призмы являются параллелограммами

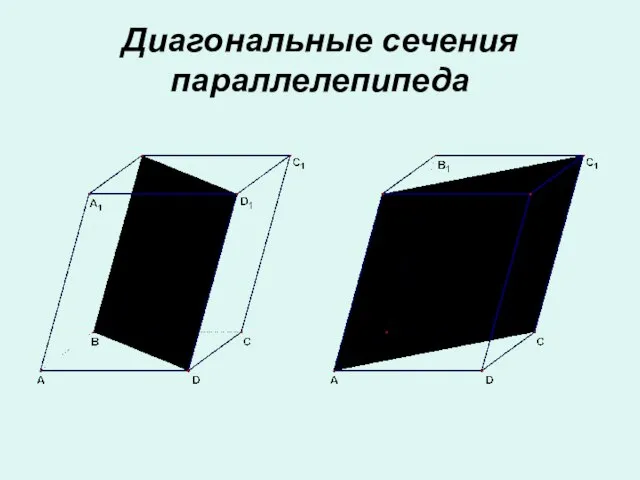
Диагональные сечения
параллелепипеда

Площадь поверхности призмы
Площадью полной поверхности призмы называется сумма площадей всех её граней
Площадью боковой поверхности призмы называется сумма площадей её боковых граней

Теорема о площади боковой поверхности прямой призмы
Теорема.
Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы

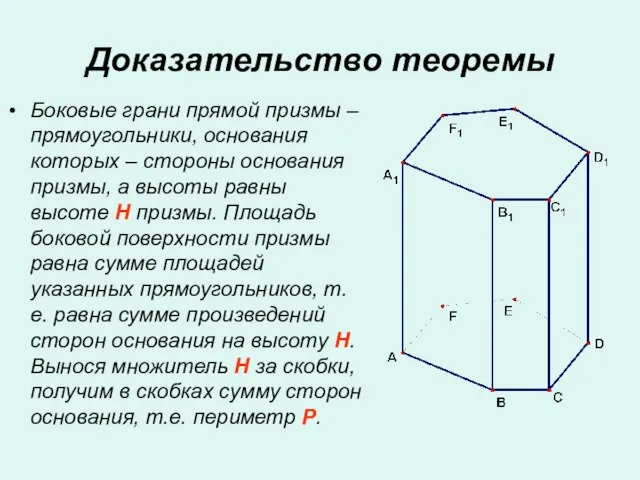
Доказательство теоремы
Боковые грани прямой призмы – прямоугольники, основания которых – стороны основания призмы, а высоты равны высоте H призмы. Площадь боковой поверхности призмы равна сумме площадей указанных прямоугольников, т.е. равна сумме произведений сторон основания на высоту H. Вынося множитель H за скобки, получим в скобках сумму сторон основания, т.е. периметр P.