Содержание
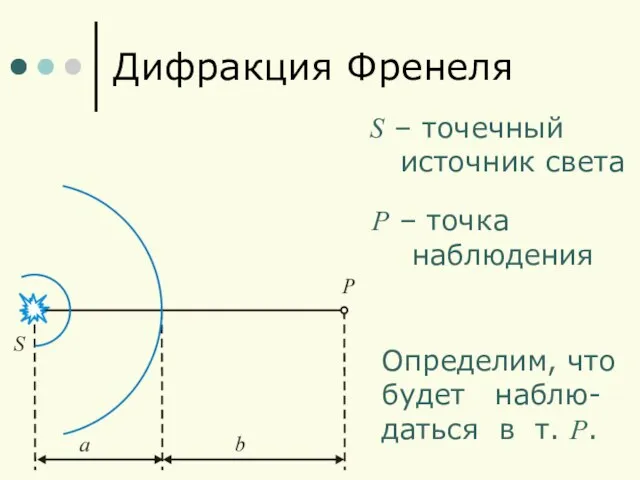
- 2. Дифракция Френеля S – точечный источник света P – точка наблюдения Определим, что будет наблю- даться
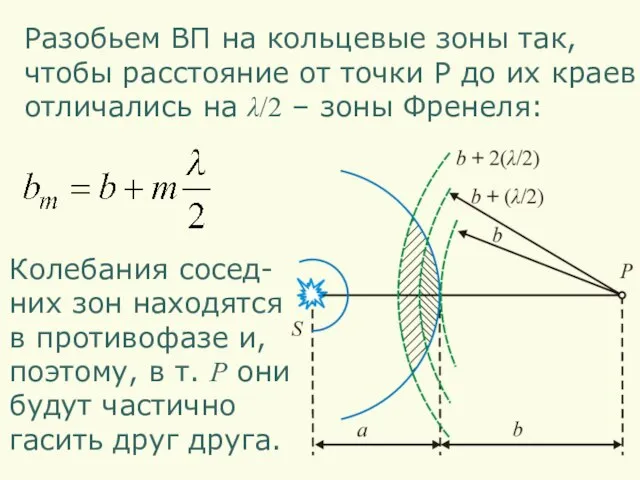
- 3. Разобьем ВП на кольцевые зоны так, чтобы расстояние от точки P до их краев отличались на
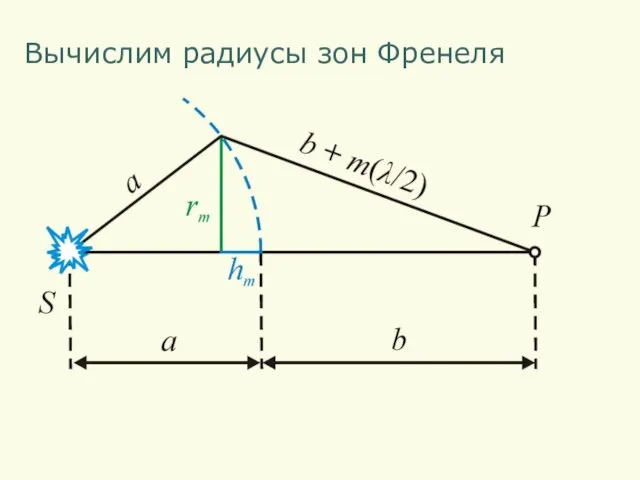
- 4. Вычислим радиусы зон Френеля
- 6. – высота сферического сегмента, занимаемого зоной с номером m – радиус m-ой зоны Френеля Площадь сферического
- 7. Площадь m-ой зоны: т.е. площади зон Френеля практически одинаковы и энергия, переносимая каждой зоной в отдельности,
- 8. Вычислим амплитуду в т.P, которая получается при сложении всех зон и учтем, что зоны находятся в
- 9. Например, радиус первой зоны при a =∞ (плоский в.ф.), b = 1 м получаем r1 =
- 10. Зонная пластинка
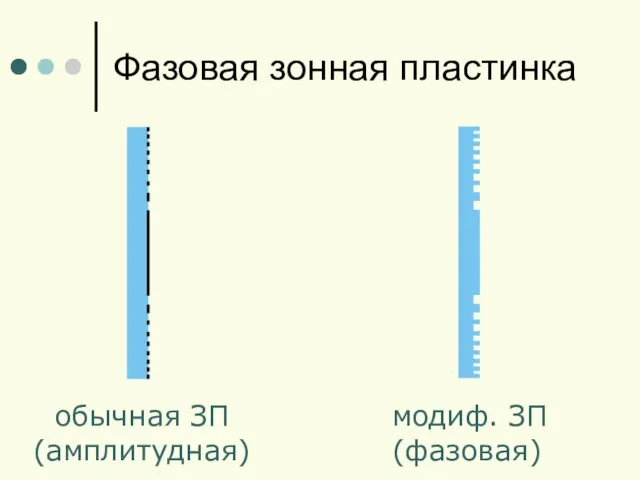
- 11. Фазовая зонная пластинка обычная ЗП (амплитудная) модиф. ЗП (фазовая)
- 12. Дифракция рентгеновских лучей Естественные 3х мерные периодические структуры – кристаллы (d = 1–4 Å = =
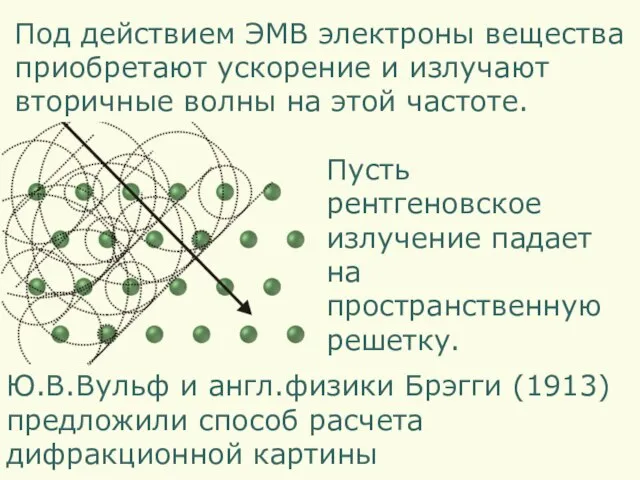
- 13. Пусть рентгеновское излучение падает на пространственную решетку. Ю.В.Вульф и англ.физики Брэгги (1913) предложили способ расчета дифракционной
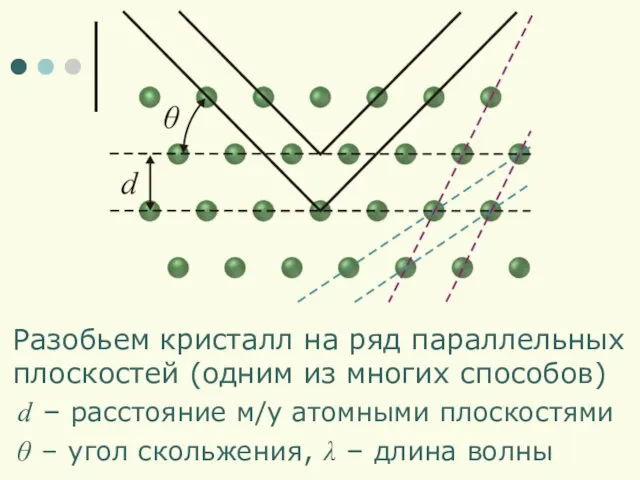
- 14. Разобьем кристалл на ряд параллельных плоскостей (одним из многих способов) d – расстояние м/у атомными плоскостями
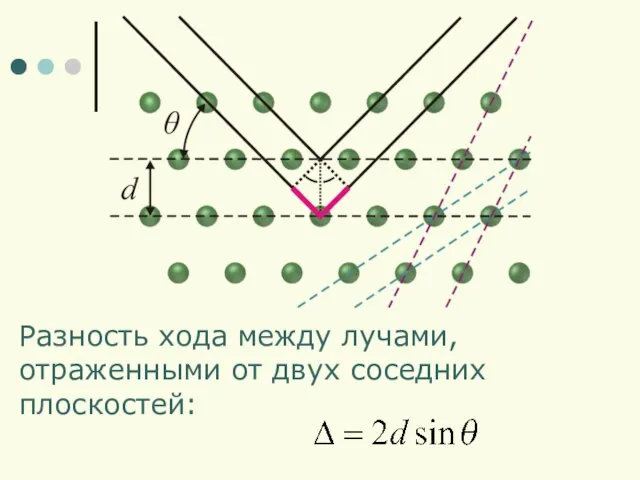
- 15. Разность хода между лучами, отраженными от двух соседних плоскостей:
- 16. Условие наилучшего отражения:
- 17. Применение явления дифракции света на кристаллах 1) В рентгеновской спектроскопии для исследования характеристик излучения 2) В
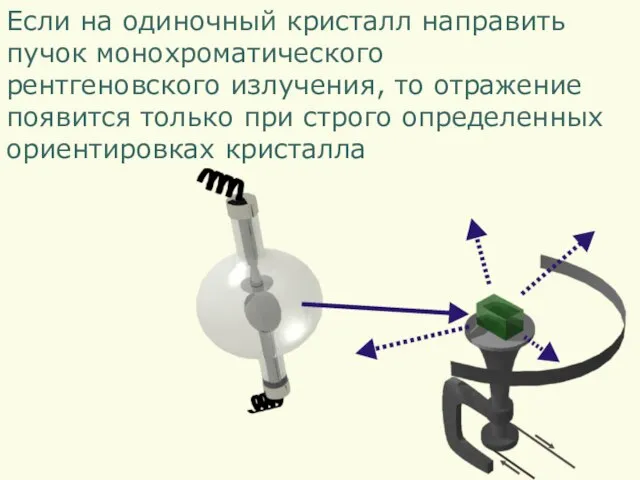
- 18. Если на одиночный кристалл направить пучок монохроматического рентгеновского излучения, то отражение появится только при строго определенных
- 19. Метод порошков Если взять поликристаллический образец (много кристалликов, спрессованных или спеченных), то для любого направления находится
- 21. Скачать презентацию
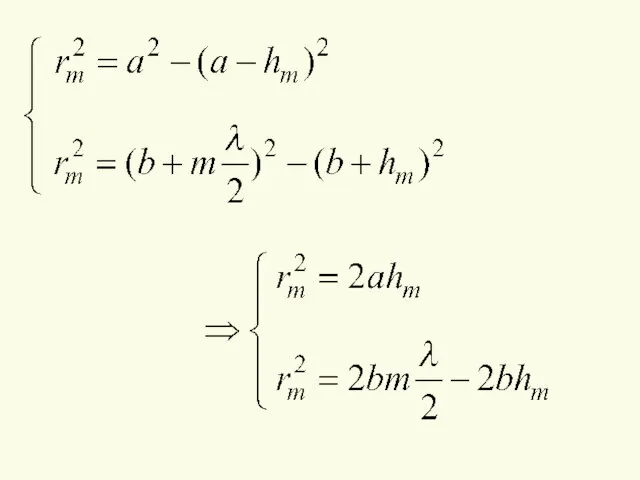









 Развитие сети профессиональных юридических услуг в России и СНГ Альберт Еганян, к.ю.н., MCIArb, Управляющий партнер
Развитие сети профессиональных юридических услуг в России и СНГ Альберт Еганян, к.ю.н., MCIArb, Управляющий партнер Kochen deutscher Kartoffelsalat
Kochen deutscher Kartoffelsalat Схемотехника. Практика 1
Схемотехника. Практика 1 Выдающиеся писатели России
Выдающиеся писатели России Китай: сопротивление реформам
Китай: сопротивление реформам Безопасность жизнедеятельности
Безопасность жизнедеятельности Одеяло Земли
Одеяло Земли Выполнила студентка 4 курса филологического факультета КГПИ Дуркина Юлия 2010
Выполнила студентка 4 курса филологического факультета КГПИ Дуркина Юлия 2010 Презентация на тему Скандинавская мифология
Презентация на тему Скандинавская мифология  Методы решения
Методы решения CX 8000 Operator Training
CX 8000 Operator Training Сервер Flash-вещаний (RTMP) на Python или создание высоконагруженных сетевых серверов с использованием Twisted
Сервер Flash-вещаний (RTMP) на Python или создание высоконагруженных сетевых серверов с использованием Twisted Ионная химическая связь
Ионная химическая связь ВАНЯ ДР-2022
ВАНЯ ДР-2022 Stili_rechi_ISP9-21_Sidorov
Stili_rechi_ISP9-21_Sidorov Общие правила выполнения зарядки в домашних условиях
Общие правила выполнения зарядки в домашних условиях Презентация на тему Королева Елизавета II
Презентация на тему Королева Елизавета II  Фигуры вращения
Фигуры вращения Общественное движение при Александре 2
Общественное движение при Александре 2 Гражданское право РФ. Право собственности и иные вещные права
Гражданское право РФ. Право собственности и иные вещные права Золотая теорема геометрии
Золотая теорема геометрии Глобус Гурмэ. Ежегодный каталог
Глобус Гурмэ. Ежегодный каталог Результативность образовательного процесса в системе дополнительного образования детей
Результативность образовательного процесса в системе дополнительного образования детей Презентация на тему Презентация - Победа. Итоги Великой Отечественной и второй Мировой войны
Презентация на тему Презентация - Победа. Итоги Великой Отечественной и второй Мировой войны Предметы народных промыслов в повседневной жизни
Предметы народных промыслов в повседневной жизни ДРЕВНИЕ
ДРЕВНИЕ Dollar
Dollar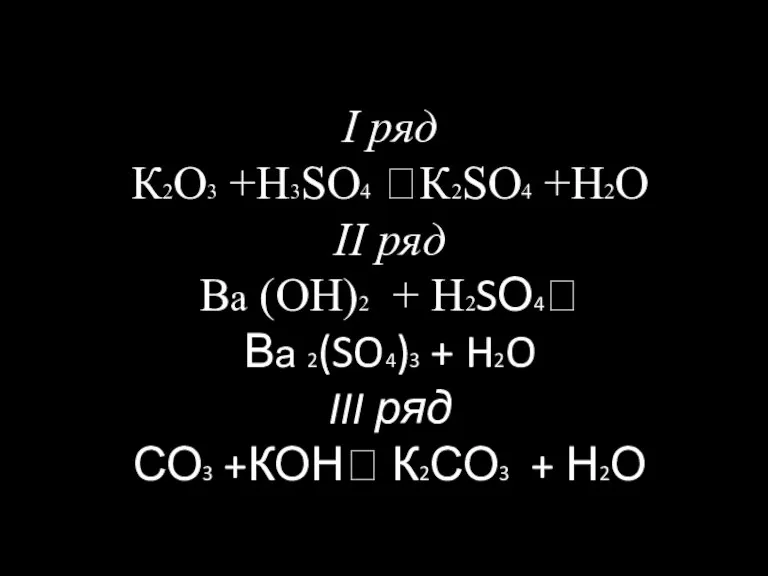 Генетические связи между важнейшими классами неорганических соединений
Генетические связи между важнейшими классами неорганических соединений