Презентация на тему Молекулярная физика Реальные газы. Пар и свойства жидкости.

Задача.
Идеальный газ, масса которого m и молярная масса μ, расширяется изобарно при некотором давлении. Начальная температура газа Т1, конечная Т2. Определить работу, совершаемую газом.
Решение.
Работа в изобарном процессе:
Из уравнения Менделеева—Клапейрона:
Ответ:

Задача.
Гелий (Не) нагревается при постоянном давлении. При этом ему сообщено Q = 20 кДж теплоты. Определить изменение внутренней энергии газа и совершенную им работу.
Решение.
Так как по условию задачи р = const, то совершаемая газом работа
Гелий — одноатомный газ, поэтому его внутренняя энергия
а ее изменение
Запишем первый закон термодинамики для этого процесса:

Следовательно:
Ответ:

Задача.
Определите давление воздуха в камере сгорания дизельного двигателя при температуре 512 °C, если плотность воздуха равна 1,8 кг/м3.
Решение.
Из уравнения Менделеева-Клапейрона
и соотношения
имеем
Учитывая, что
Получим
Ответ: P=4 МПа.

Задача.
Как изменится абсолютная температура идеального газа при уменьшении его объема в 2 раза и увеличении давления в 3 раза?
Решение:
Из уравнения Менделеева-Клапейрона
и соотношений
получаем
Ответ: абсолютная температура идеального газа приуменьшении его объема в 2 раза и увеличении давления в 3 раза увеличится в 1,5 раза.

Реальные газы
Реальный газ — газ, который не описывается уравнением состояния идеального газа Клапейрона — Менделеева.
Зависимости между его параметрами показывают, что молекулы в реальном газе взаимодействуют между собой и занимают определенный объём. Состояние реального газа часто на практике описывается уравнением Ван-дер-Ваальса (для одного моля газа):
Постоянные a и b определяются экспериментально и имеют различные значения для разного сорта молекул.
Рассмотрим сначала газ, в котором частицы не взаимодействуют друг с другом, такой газ удовлетворяет уравнению состояния идеального газа:

Далее предположим, что частицы данного газа являются упругими сферами одинакового радиуса r. Так как газ находится в сосуде конечного объёма, то пространство, где могут перемещаться частицы, будет несколько меньше. В исходной формуле следует вычесть из всего объёма некую его часть b, которая, вообще говоря, зависит только от вещества, из которого состоит газ. Таким образом, получается следующее уравнение:
Далее Ван-дер-Ваальс рассматривает силы притяжения между частицами газа и делает следующие допущения:
Частицы распределёнными равномерно по всему объёму.
Силы притяжения стенок сосуда не учитываются.
Частицы, находящиеся внутри сосуда и непосредственно у стенок, ощущают притяжение по-разному: внутри сосуда действующие силы притяжения других частиц компенсируют друг друга.

С учетом этих допущений можно считать, что давление на стенки сосуда меньше на некоторую величину, обратно пропорциональную квадрату объёма:
Окончательное уравнение:
На рис. приведены изотермы, вычисленные по уравнению Ван-дер-Ваальса для диоксида углерода.
Согласно правилу Максвелла (для того, чтобы расчетная кривая соответствовала экспериментальной равновесной изотерме, нужно вместо кривой 12345 провести горизонтальную прямую 15 так, чтобы площади 1231 и 3453 были равны.

Ян Дидерик Ван-дер-Ваа́льс (1837 - 1923) — голландский физик, лауреат Нобелевской премии по физике в 1910 г.
Большая часть работ Ван-дер-Ваальса относится к области теоретической молекулярной физики. Он исследовал поведение молекул и занимался теориями, описывающими состояния материи.
В 1869 году он открыл силы взаимодействия между молекулами, которые впоследствии были названы его именем — силы Ван-дер-Ваальса.
На основе этой модели он вывел уравнение состояния реального газа.
За это достижение Ван-дер-Ваальс получил в 1910 г. Нобелевскую премию по физике «за работу над уравнением состояния газов и жидкостей».

Медленно будем сжимать газ в сосуде с поршнем, например углекислый газ (СO2).
Сжимая его, мы выполняем над ним работу, вследствие чего внутренняя энергия газа увеличится. Когда мы хотим, чтобы процесс происходил при постоянной температуре, то сжимать газ надо очень медленно, чтобы теплота успевала переходить от газа в окружающую среду.
Выполняя этот опыт, можно заметить, что сначала при большом объёме давление с уменьшением объёма увеличивается согласно закону Бойля — Мариотта.

В конце концов, начиная с какого-то значения, давление не будет изменяться, несмотря на уменьшение объёма. На стенках цилиндра и поршня образуются прозрачные капли. Это означает, что газ начал конденсироваться, то есть переходить в жидкое состояние.
Продолжая сжимать содержимое цилиндра, мы будем увеличивать массу жидкости под поршнем и соответственно, будем уменьшать массу газа. Давление, которое показывает манометр, будет оставаться постоянным до тех пор, пока всё пространство под поршнем не заполнит жидкость.
Жидкости мало сжимаемы. Поэтому дальше, даже при незначительном уменьшении объёма, давление быстро будет возрастать.
Поскольку весь процесс происходит при постоянной температуре T, кривую, что изображает зависимость давления р от объёма V, называют изотермой.
При некотором объёме V1 начинается конденсация газа, а при объёме V2 она заканчивается. Если V > V1 то вещество будет в газообразном состоянии, а при V < V2 — в жидком.
Опыты показывают, что такой вид имеют изотермы и всех других газов, если их температура не очень высокая.

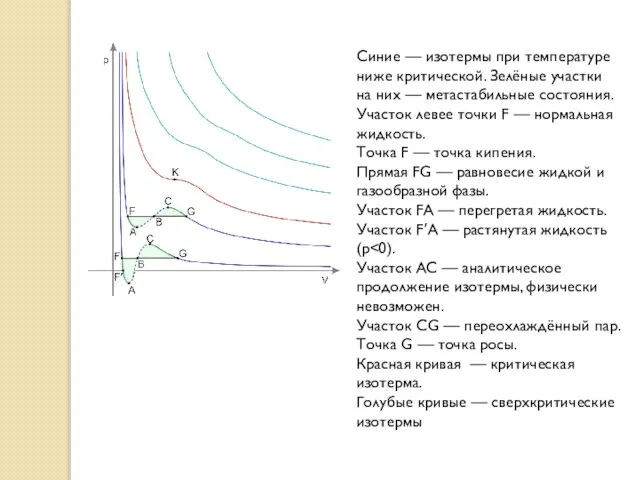
Синие — изотермы при температуре ниже критической. Зелёные участки на них — метастабильные состояния.
Участок левее точки F — нормальная жидкость.
Точка F — точка кипения.
Прямая FG — равновесие жидкой и газообразной фазы.
Участок FA — перегретая жидкость.
Участок F′A — растянутая жидкость (p<0).
Участок AC — аналитическое продолжение изотермы, физически невозможен.
Участок CG — переохлаждённый пар.
Точка G — точка росы.
Красная кривая — критическая изотерма.
Голубые кривые — сверхкритические изотермы

Опыты показывают, что такой вид имеют изотермы и всех других газов, если их температура не очень высокая.
В этом процессе, когда газ превращается в жидкость при изменении его объёма от V1 к V2, давление газа остаётся постоянным. Каждой точке прямолинейной части изотермы 1—2 соответствует равновесие между газообразным и жидким состояниями вещества. Это означает, что при определённых T и V количество жидкости и газа над ней остаётся неизменным. Равновесие имеет динамический характер: количество молекул, которые покидают жидкости, в среднем равняется количеству молекул, которые переходят из газа в жидкость за одно и то же время.
Также существует такое понятие как критическая температура, если газ находится при температуре выше критической (индивидуальна для каждого газа, например для углекислого газа примерно 304 К), то его уже невозможно превратить в жидкость, какое бы давление к нему не прилагалось.
Данное явление возникает вследствие того, что при критической температуре силы поверхностного натяжения жидкости равны нулю.

Пар
Пар — газообразное состояние вещества в условиях, когда газовая фаза может находиться в равновесии с жидкой или твёрдой фазами того же вещества.
Процесс возникновения пара из жидкой (твёрдой) фазы называется парообразованием. Обратный процесс называется конденсация.
При низких давлениях и высоких температурах свойства пара приближаются к свойствам идеального газа. В разговорной речи под словом «пар» почти всегда понимают водяной пар. Пары́ прочих веществ оговариваются в явном виде. Не следует путать оптически однородный и гомогенный пар с туманом — гетерогенной системой, сильно рассеивающей свет.
Различают следующие виды состояний пара:
Ненасыщенный пар — пар, не достигший термодинамического равновесия со своей жидкостью. При данной температуре давление ненасыщенного пара всегда меньше давления насыщенного пара. При наличии над поверхностью жидкости ненасыщенного пара процесс парообразования преобладает над процессом конденсации, и потому жидкости в сосуде с течением времени становится все меньше и меньше.
Насы́щенный пар — это пар, находящийся в термодинамическом равновесии с жидкостью.

У разных жидкостей насыщение пара - динамическое равновесие с паром - наступает при различной плотности и давлении пара. Причина этого заключается в различии сил межмолекулярного взаимодействия.
В жидкостях, у которых силы межмолекулярного притяжения велики, например у ртути, только наиболее быстрые молекулы, число которых незначительно, могут вылетать из жидкости. Поэтому для таких жидкостей уже при небольшой плотности пара наступает состояние равновесия.
У жидкостей с малой силой притяжения молекул, например у эфира, при той же температуре может вылететь за пределы жидкости множество молекул. Поэтому и равновесное состояние наступает только при значительной плотности пара.

Свойства жидкостей
Поверхностное натяжение
Молекулы вещества в жидком состоянии расположены почти вплотную друг к другу.
В отличие от газов, где молекулы находятся на больших расстояниях друг от друга, двигаются хаотично и не взаимодействую, и от твердых кристаллических тел, в которых молекулы образуют упорядоченные структуры во всем объеме кристалла и могут совершать тепловые колебания около фиксированных центров, молекулы жидкости обладают большей свободой.
Каждая молекула жидкости, также как и в твердом теле, «зажата» со всех сторон соседними молекулами и совершает тепловые колебания около некоторого положения равновесия. Однако, время от времени любая молекула может переместиться в соседнее вакантное место.

Такие перескоки в жидкостях происходят довольно часто; поэтому молекулы не привязаны к определенным центрам, как в кристаллах , и могут перемещаться по всему объему жидкости. Этим объясняется текучесть жидкостей. Из-за сильного взаимодействия между близко расположенными молекулами они могут образовывать локальные (неустойчивые) упорядоченные группы, содержащие несколько молекул. Это явление называется ближним порядком .
Рис. иллюстрирует отличие газообразного вещества от жидкости на примере воды.
Молекула воды H2O состоит из одного атома кислорода и двух атомов водорода, расположенных под углом 104°. Среднее расстояние между молекулами пара в десятки раз превышает среднее расстояние между молекулами воды.

Вследствие плотной упаковки молекул сжимаемость жидкостей, т. е. изменение объема при изменении давления, очень мала; она в десятки и сотни тысяч раз меньше, чем в газах. Например, для изменения объема воды на 1 % нужно увеличить давление приблизительно в 200 раз. Такое увеличение давления по сравнению с атмосферным достигается на глубине около 2 км.
Жидкости, как и твердые тела, изменяют свой объем при изменении температуры. Для не очень больших интервалов температур относительное изменение объема ΔV / V0 пропорционально изменению температуры ΔT:
Коэффициент β называют температурным коэффициентом объемного расширения. Этот коэффициент у жидкостей в десятки раз больше, чем у твердых тел.

Тепловое расширение воды имеет интересную и важную для жизни на Земле аномалию. При температуре ниже 4 °С вода расширяется при понижении температуры (β < 0). Максимум плотности ρв = 103 кг/м3 вода имеет при температуре 4 °С.
При замерзании вода расширяется, поэтому лед остается плавать на поверхности замерзающего водоема. Температура замерзающей воды подо льдом равна 0 °С. В более плотных слоях воды у дна водоема температура оказывается порядка 4 °С. Благодаря этому жизнь может существовать в воде замерзающих водоемов.

Наиболее интересной особенностью жидкостей является наличие свободной поверхности.
Жидкость, в отличие от газов, не заполняет весь объем сосуда, в который она налита. Между жидкостью и газом (или паром) образуется граница раздела, которая находится в особых условиях по сравнению с остальной массой жидкости. Молекулы в пограничном слое жидкости, в отличие от молекул в ее глубине, окружены другими молекулами той же жидкости не со всех сторон. Силы межмолекулярного взаимодействия, действующие на одну из молекул внутри жидкости со стороны соседних молекул, в среднем взаимно скомпенсированы. Любая молекула в пограничном слое притягивается молекулами, находящимися внутри жидкости (силами, действующими на данную молекулу жидкости со стороны молекул газа (или пара) можно пренебречь). В результате появляется некоторая равнодействующая сила, направленная вглубь жидкости.

Поверхностные молекулы силами межмолекулярного притяжения втягиваются внутрь жидкости. Но все молекулы, в том числе и молекулы пограничного слоя, должны находиться в состоянии равновесия. Это равновесие достигается за счет некоторого уменьшения расстояния между молекулами поверхностного слоя и их ближайшими соседями внутри жидкости, то есть молекулы поверхностного слоя упакованы несколько более плотно, а поэтому они обладают дополнительным запасом потенциальной энергии по сравнению с внутренними молекулами.
Чтобы вытащить некоторое количество молекул из глубины жидкости на поверхность (т. е. увеличить площадь поверхности жидкости), внешние силы должны совершить работу ΔAвнеш , пропорциональную изменению ΔS площади поверхности:
ΔAвнеш = σΔS
Коэффициент σ называется коэффициентом поверхностного натяжения (σ > 0). Таким образом, коэффициент поверхностного натяжения равен работе, необходимой для увеличения площади поверхности жидкости при постоянной температуре на единицу.

Следовательно, молекулы поверхностного слоя жидкости обладают избыточной по сравнению с молекулами внутри жидкости потенциальной энергией. Потенциальная энергия Eп поверхности жидкости пропорциональна ее площади:
Eп = Aвнеш = σS
Из механики известно, что равновесным состояниям системы соответствует минимальное значение ее потенциальной энергии. Отсюда следует, что свободная поверхность жидкости стремится сократить свою площадь. По этой причине свободная капля жидкости принимает шарообразную форму. Жидкость ведет себя так, как будто по касательной к ее поверхности действуют силы, сокращающие (стягивающие) эту поверхность. Эти силы называются силами поверхностного натяжения.

Некоторые жидкости, как, например, мыльная вода, обладают способностью образовывать тонкие пленки.
Всем хорошо известные мыльные пузыри имеют правильную сферическую форму – в этом тоже проявляется действие сил поверхностного натяжения. Если в мыльный раствор опустить проволочную рамку, одна из сторон которой подвижна, то вся она затянется пленкой жидкости.
Силы поверхностного натяжения стремятся сократить поверхность пленки. Для равновесия подвижной стороны рамки к ней нужно приложить внешнюю силу Fвн. Если под действием силы перекладина переместится на Δx, то будет произведена работа ΔAвн = FвнΔx = ΔEп = σΔS, где ΔS = 2LΔx – приращение площади поверхности обеих сторон мыльной пленки.

Отсюда получаем
Таким образом, коэффициент поверхностного натяжения σ может быть определен как модуль силы поверхностного натяжения, действующей на единицу длины линии, ограничивающей поверхность.
Из-за действия сил поверхностного натяжения в каплях жидкости и внутри мыльных пузырей возникает избыточное давление Δp. Если мысленно разрезать сферическую каплю радиуса R на две половинки, то каждая из них должна находиться в равновесии под действием сил поверхностного натяжения, приложенных к границе разреза длиной 2πR и сил избыточного давления, действующих на площадь πR2 сечения. Условие равновесия записывается в виде
σ2πR = ΔpπR2. Отсюда избыточное давление внутри капли равно

Вблизи границы между жидкостью, твердым телом и газом форма свободной поверхности жидкости зависит от сил взаимодействия молекул жидкости с молекулами твердого тела (взаимодействием с молекулами газа (или пара) можно пренебречь).
Если эти силы больше сил взаимодействия между молекулами самой жидкости, то жидкость смачивает поверхность твердого тела. В этом случае жидкость подходит к поверхности твердого тела под некоторым острым углом θ, характерным для данной пары жидкость – твердое тело. Угол θ называется краевым углом.
Если силы взаимодействия между молекулами жидкости превосходят силы их взаимодействия с молекулами твердого тела, то краевой угол θ оказывается тупым. В этом случае говорят, что жидкость не смачивает поверхность твердого тела.
При полном смачивании θ = 0, при полном несмачивании θ = 180°.

Капиллярными явлениями называют подъем или опускание жидкости в трубках малого диаметра – капиллярах. Смачивающие жидкости поднимаются по капиллярам, несмачивающие – опускаются.
На рис. изображена капиллярная трубка некоторого радиуса r, опущенная нижним концом в смачивающую жидкость плотности ρ.
Верхний конец капилляра открыт. Подъем жидкости в капилляре продолжается до тех пор, пока сила тяжести действующая на столб жидкости в капилляре, не станет равной по модулю результирующей Fн сил поверхностного натяжения, действующих вдоль границы соприкосновения жидкости с поверхностью капилляра: Fт = Fн, где Fт = mg = ρhπr2g, Fн = σ2πr cos θ.
Отсюда следует:

При полном смачивании θ = 0, cos θ = 1. В этом случае
При полном несмачивании θ = 180°, cos θ = –1 и, следовательно, h < 0. Уровень несмачивающей жидкости в капилляре опускается ниже уровня жидкости в сосуде, в которую опущен капилляр.
Вода практически полностью смачивает чистую поверхность стекла. Наоборот, ртуть полностью не смачивает стеклянную поверхность. Поэтому уровень ртути в стеклянном капилляре опускается ниже уровня в сосуде.

В 1643 г. по предложению итальянского физика Эванджелисты Торричелли (1608—1647) был произведен следующий опыт. Стеклянную трубку длины около 1 м, запаянную с. одного конца, наполняют ртутью. Отверстие трубки закрывают пальцем, чтобы ртуть не вылилась, и трубку опускают в вертикальном положении отверстием вниз в сосуд с ртутью. Если теперь отнять палец от отверстия трубки, то столб ртути упадет до высоты около 760 мм над уровнем ртути в сосуде.
На свободную поверхность ртути в сосуде действует атмосферное давление. Так как после опускания ртути в трубке над ртутью остается пустота, то давление столба ртути, создаваемое внутри трубки на уровне поверхности ртути в сосуде, должно равняться атмосферному давлению.

Поэтому взятая в миллиметрах высота столба над свободной поверхностью ртути прямо измеряет давление атмосферы в миллиметрах ртутного столба. Таким образом, трубка Торричелли может служить для измерения давления атмосферы. Она играет роль «барометра».
Итак, опыт показывает, что атмосферное давление составляет около 760 мм рт. ст. Так как 1 мм рт. ст.= 13,6 мм вод. ст., то атмосферное давление равно 760•13,6 мм вод. ст.=10 332 мм вод. ст. = 1,013•105 Па, таким образом, атмосферное давление равно давлению столба воды высоты больше 10 м.
При изменении атмосферного давления меняется и высота столба ртути в трубке. При увеличении давления столбик удлиняется — «барометр поднимается». При уменьшении давления «барометр падает» — столб ртути уменьшает свою высоту.
Пространство над столбом ртути в трубке в опыте Торричелли называют торричеллиевой пустотой.

Закон Паскаля
Закон Паскаля формулируется так:
Возмущение давления, производимое на покоящуюся несжимаемую жидкость, передается в любую точку жидкости одинаково по всем направлениям. Жидкости передают производимое на них давление одинаково по всем направлениям.
Закон сформулирован французским учёным Блезом Паскалем.
Формула закона Паскаля и его применение.
Закон Паскаля описывается формулой давления:
p=F/S,
где p – это давление, F – приложенная сила, S – площадь сосуда.
Из формулы мы видим, что при увеличении силы воздействия при той же площади сосуда давление на его стенки будет увеличиваться. Измеряется давление в ньютонах на метр квадратный или в паскалях (Па), в честь ученого, открывшего закон Паскаля.

По указанию Паскаля, крепкую дубовую бочку до краев наполнили водой и наглухо закрыли крышкой. В небольшое отверстие в крышке заделали конец вертикальной стеклянной трубки такой длины, что конец ее оказался на уровне второго этажа.
Выйдя на балкон, Паскаль принялся наполнять трубку водой. Не успел он вылить и десятка стаканов, как вдруг, к изумлению обступивших бочку зевак, бочка с треском лопнула. Ее разорвала непонятная сила. Паскаль убеждается: да, сила, разорвавшая бочку, вовсе не зависит от количества воды в трубке. Все дело в высоте, до которой трубка была заполнена.
Так проявляется удивительное свойство воды - передавать давление, создаваемое на ее поверхности (в бочке) по всему объему, каждой точке стенки или дна бочки.

Блез Паска́ль (1623 —1662) — французский математик, механик, физик, литератор и философ.
Классик французской литературы, один из основателей математического анализа, теории вероятностей и проективной геометрии, создатель первых образцов счётной техники, автор основного закона гидростатики.
Шестнадцати лет Блез Паскаль написал весьма примечательный трактат о конических сечениях, то есть о кривых линиях, получающихся при пересечении конуса плоскостью, — таковы эллипс, парабола и гипербола.
Сконструировал первую суммирующую машину.
Открыл, что явление подъема жидкостей в насосах и трубках обусловлено весом воздуха.
Показал, что давление жидкости распространяется во все стороны равномерно и что из этого свойства жидкостей вытекают почти все остальные их механические свойства

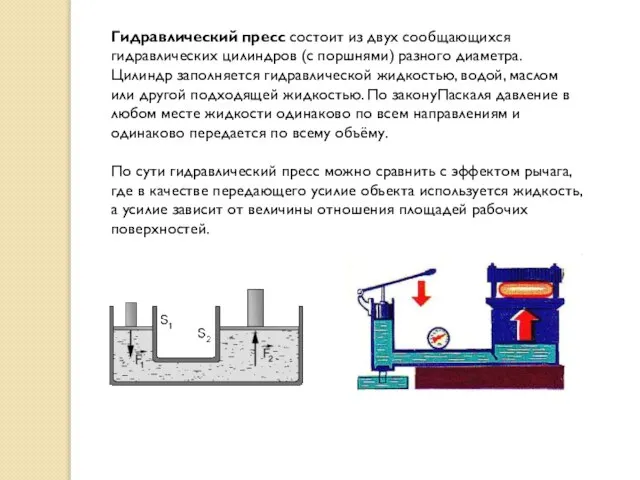
Гидравлический пресс состоит из двух сообщающихся гидравлических цилиндров (с поршнями) разного диаметра. Цилиндр заполняется гидравлической жидкостью, водой, маслом или другой подходящей жидкостью. По законуПаскаля давление в любом месте жидкости одинаково по всем направлениям и одинаково передается по всему объёму.
По сути гидравлический пресс можно сравнить с эффектом рычага, где в качестве передающего усилие объекта используется жидкость, а усилие зависит от величины отношения площадей рабочих поверхностей.

Жидкости и газы могут двигаться совершенно фантастическим образом, и для описания их поведения используются неподъемные системы дифференциальных уравнений. Но иногда физики отвлекаются от составления и решения сложных уравнений и фотографируют движущиеся жидкости и газы.
Так лопается кавитационный пузырек, созданный лазером в водяной капле

Струя жидкости, ударяющаяся о движущуюся поверхность из той же жидкости, прыгает на ней, формируя такую "змейку".

Так потоки воздуха распределяются вокруг пули, летящей с очень высокой скоростью.

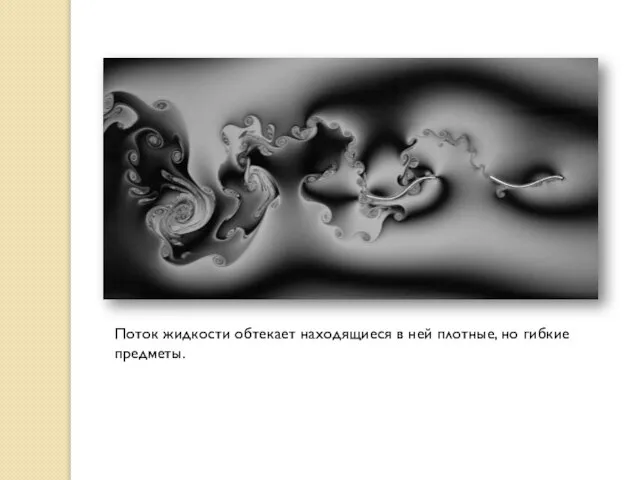
Поток жидкости обтекает находящиеся в ней плотные, но гибкие предметы.

Xолодная и плотная вода от кубика льда опускается вниз в более теплую воду.

Подобные волнообразные структуры возникают на границах потоков, движущихся с различной скоростью, и называются неустойчивостями Кельвина-Гельмгольца

Такие структуры возникают, когда жидкость небольшой вязкости (например, вода), попадает в жидкость с большей вязкостью (например, глицерин).