Содержание
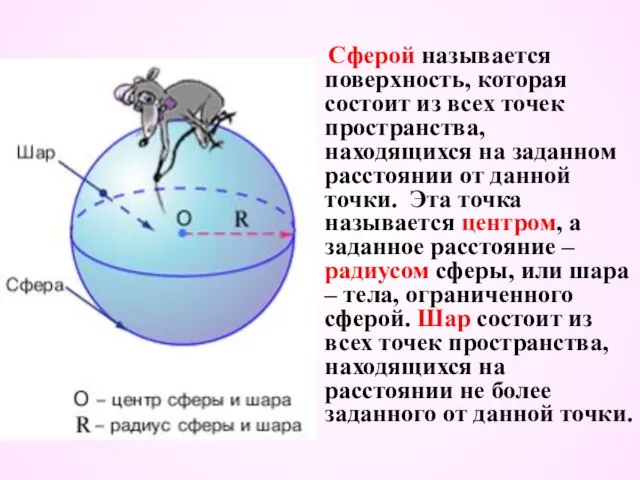
- 2. Сферой называется поверхность, которая состоит из всех точек пространства, находящихся на заданном расстоянии от данной точки.
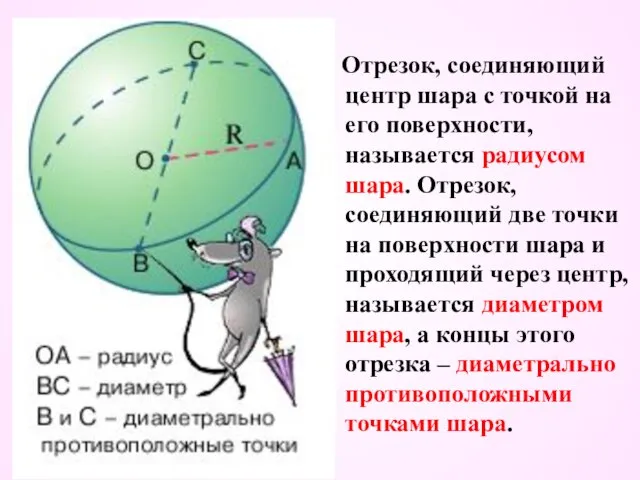
- 3. Отрезок, соединяющий центр шара с точкой на его поверхности, называется радиусом шара. Отрезок, соединяющий две точки
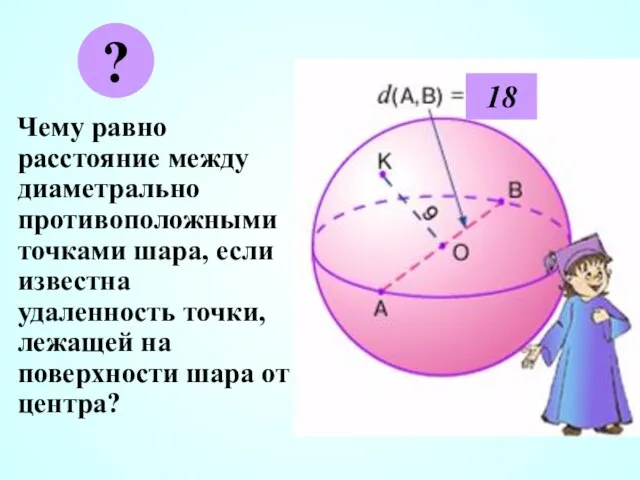
- 4. Чему равно расстояние между диаметрально противоположными точками шара, если известна удаленность точки, лежащей на поверхности шара
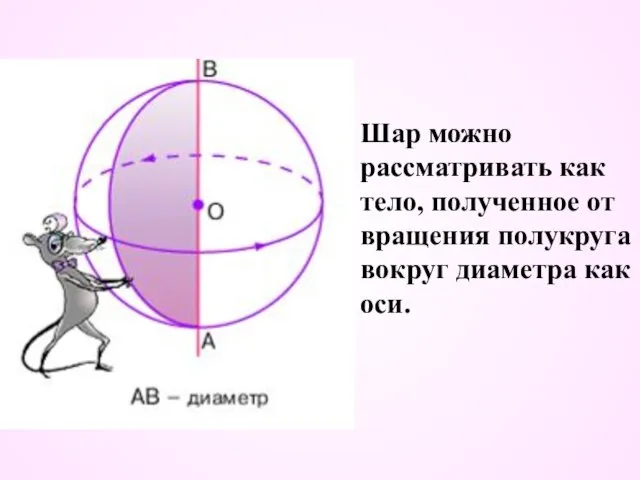
- 5. Шар можно рассматривать как тело, полученное от вращения полукруга вокруг диаметра как оси.
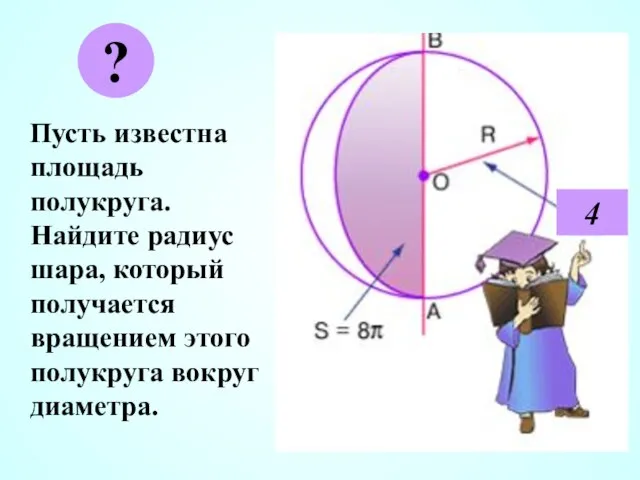
- 6. Пусть известна площадь полукруга. Найдите радиус шара, который получается вращением этого полукруга вокруг диаметра. ? 4
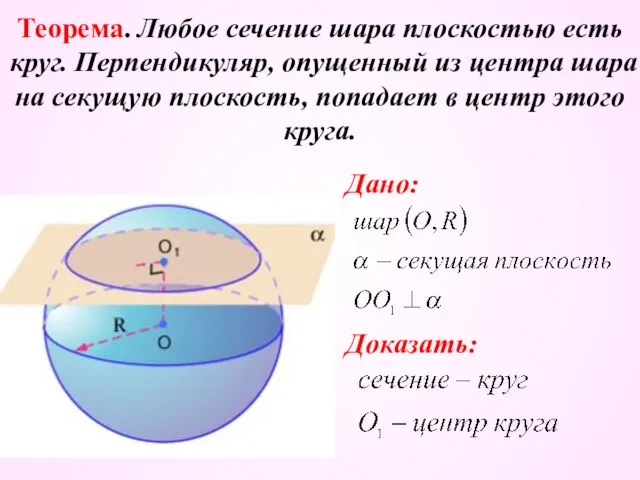
- 7. Теорема. Любое сечение шара плоскостью есть круг. Перпендикуляр, опущенный из центра шара на секущую плоскость, попадает
- 8. Доказательство: Рассмотрим прямоугольный треугольник, вершинами которого являются центр шара, основание перпендикуляра, опущенного из центра на плоскость,
- 9. Следствие. Если известны радиус шара и расстояние от центра шара до плоскости сечения, то радиус сечения
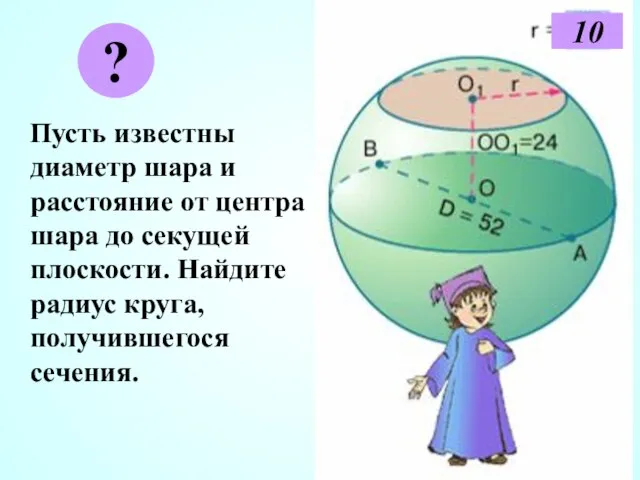
- 10. Пусть известны диаметр шара и расстояние от центра шара до секущей плоскости. Найдите радиус круга, получившегося
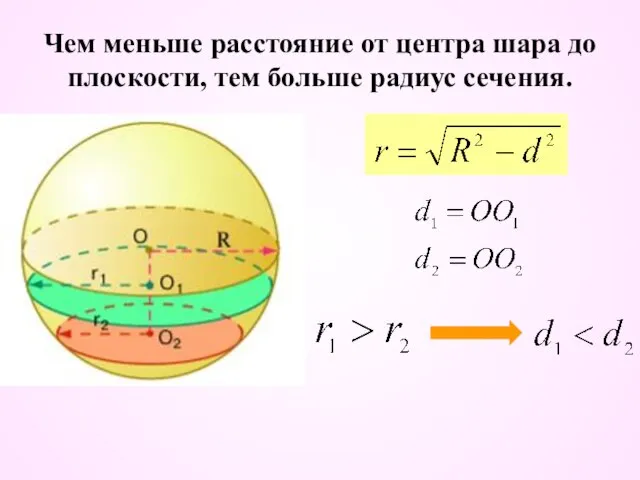
- 11. Чем меньше расстояние от центра шара до плоскости, тем больше радиус сечения.
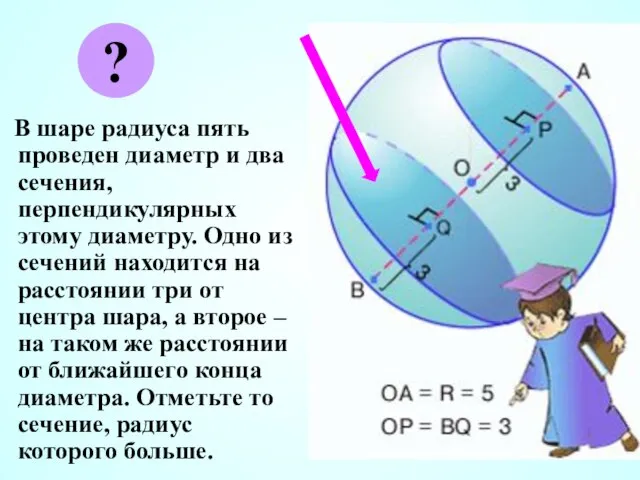
- 12. В шаре радиуса пять проведен диаметр и два сечения, перпендикулярных этому диаметру. Одно из сечений находится
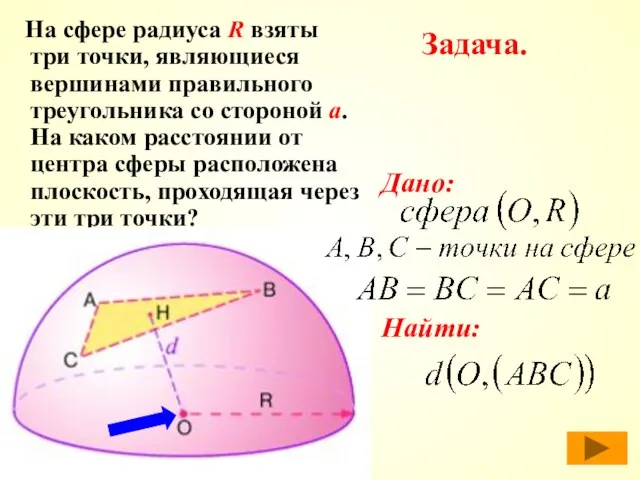
- 13. Задача. На сфере радиуса R взяты три точки, являющиеся вершинами правильного треугольника со стороной а. На
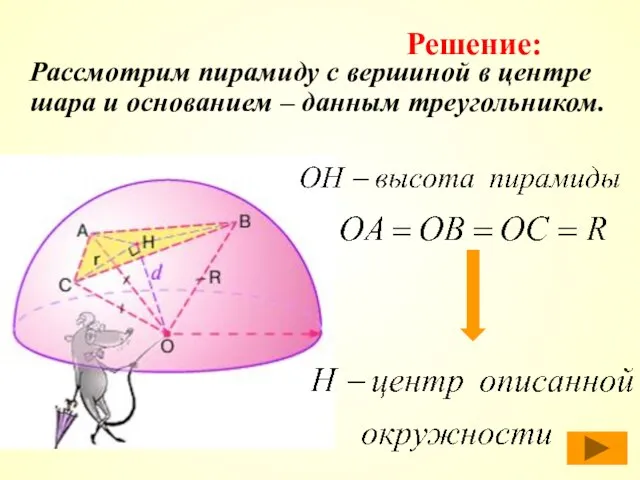
- 14. Рассмотрим пирамиду с вершиной в центре шара и основанием – данным треугольником. Решение:
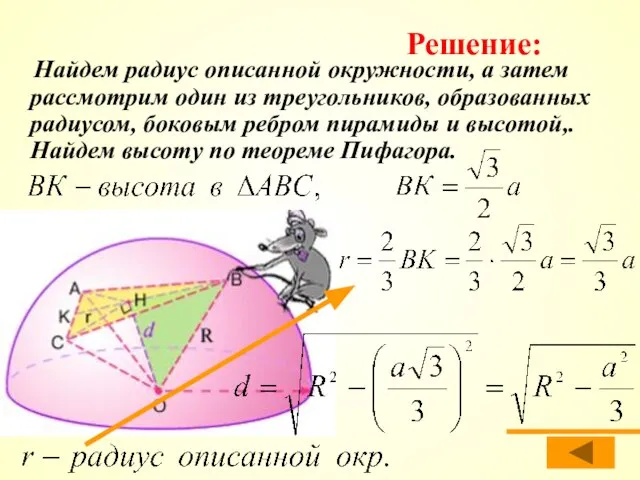
- 15. Найдем радиус описанной окружности, а затем рассмотрим один из треугольников, образованных радиусом, боковым ребром пирамиды и
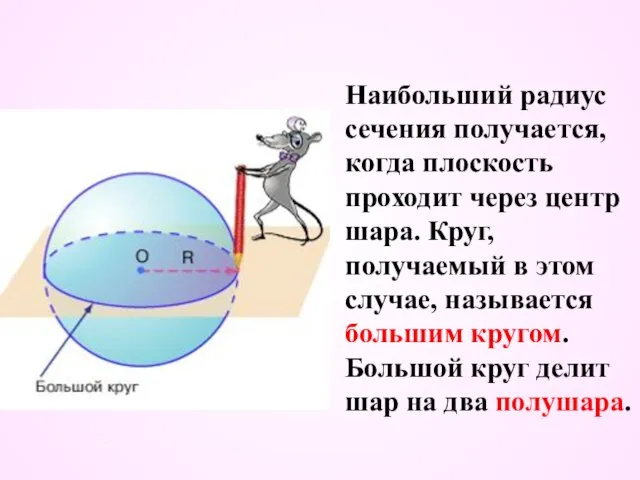
- 16. Наибольший радиус сечения получается, когда плоскость проходит через центр шара. Круг, получаемый в этом случае, называется
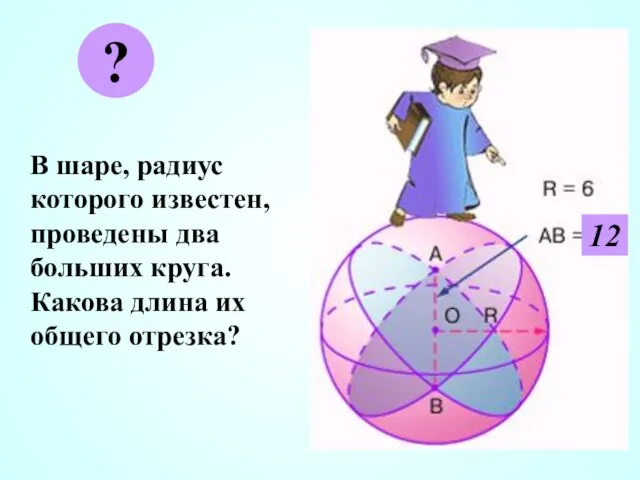
- 17. В шаре, радиус которого известен, проведены два больших круга. Какова длина их общего отрезка? ? 12
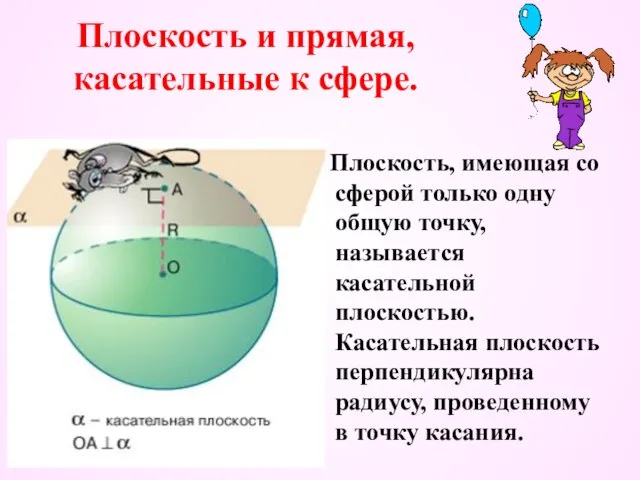
- 18. Плоскость и прямая, касательные к сфере. Плоскость, имеющая со сферой только одну общую точку, называется касательной
- 19. Пусть шар, радиус которого известен, лежит на горизонтальной плоскости. В этой плоскости через точку касания и
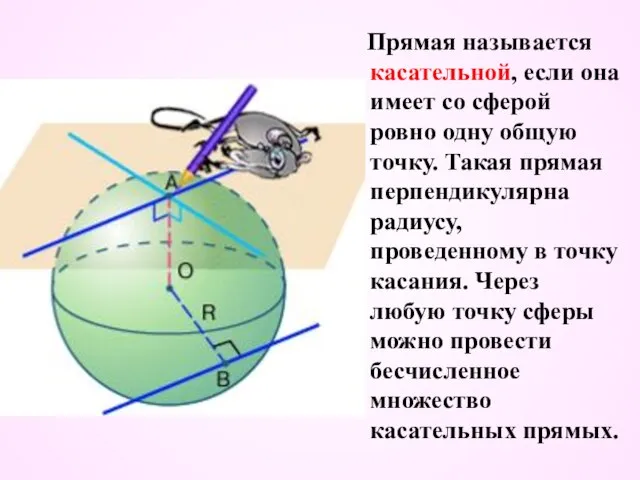
- 20. Прямая называется касательной, если она имеет со сферой ровно одну общую точку. Такая прямая перпендикулярна радиусу,
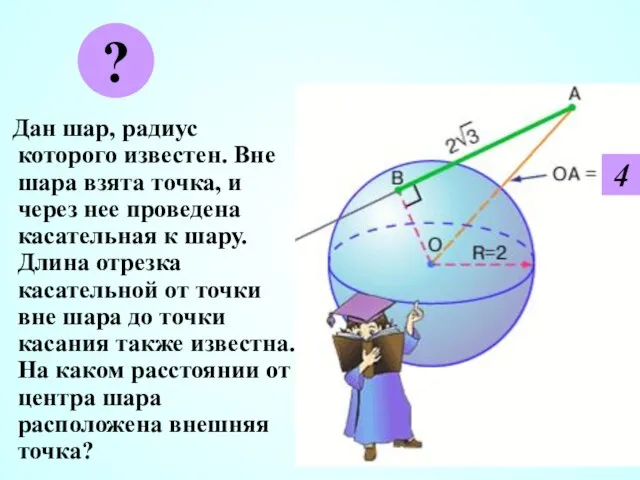
- 21. Дан шар, радиус которого известен. Вне шара взята точка, и через нее проведена касательная к шару.
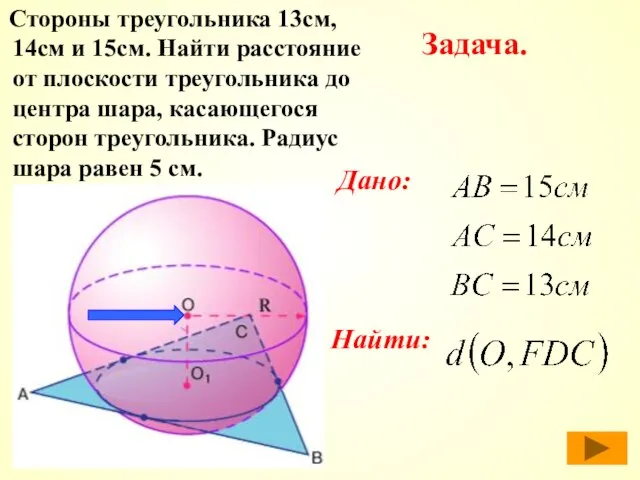
- 22. Стороны треугольника 13см, 14см и 15см. Найти расстояние от плоскости треугольника до центра шара, касающегося сторон
- 23. Сечение сферы, проходящее через точки касания, - это вписанная в треугольник АВС окружность. Решение:
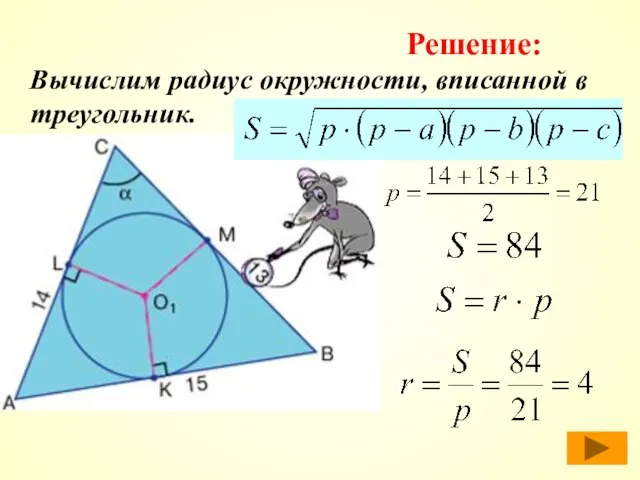
- 24. Вычислим радиус окружности, вписанной в треугольник. Решение:
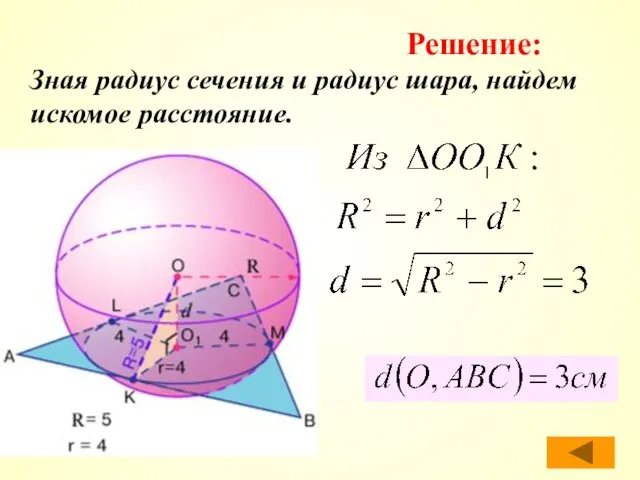
- 25. Зная радиус сечения и радиус шара, найдем искомое расстояние. Решение:
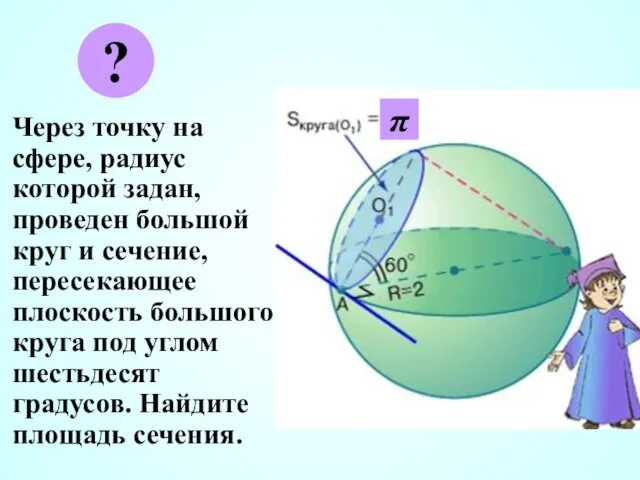
- 26. Через точку на сфере, радиус которой задан, проведен большой круг и сечение, пересекающее плоскость большого круга
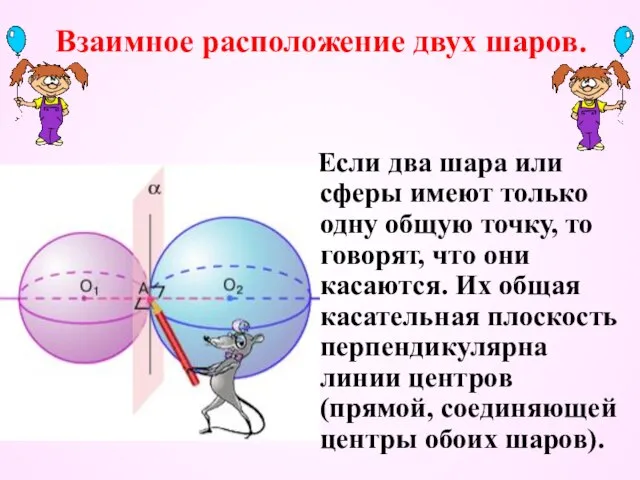
- 27. Взаимное расположение двух шаров. Если два шара или сферы имеют только одну общую точку, то говорят,
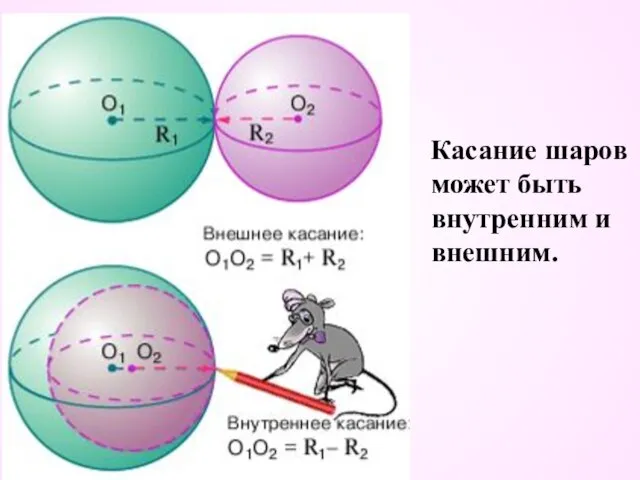
- 28. Касание шаров может быть внутренним и внешним.
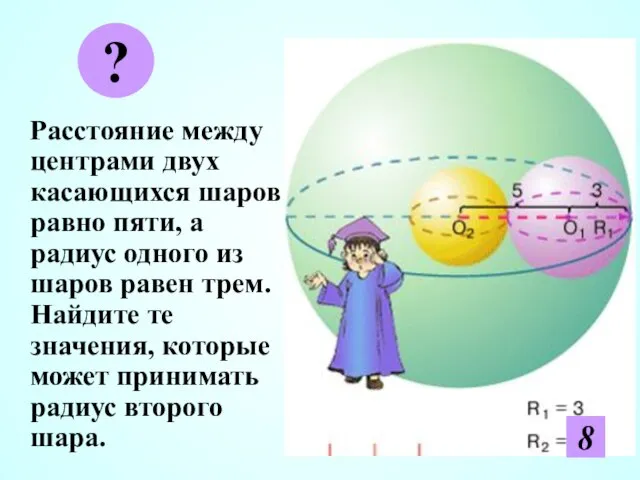
- 29. Расстояние между центрами двух касающихся шаров равно пяти, а радиус одного из шаров равен трем. Найдите
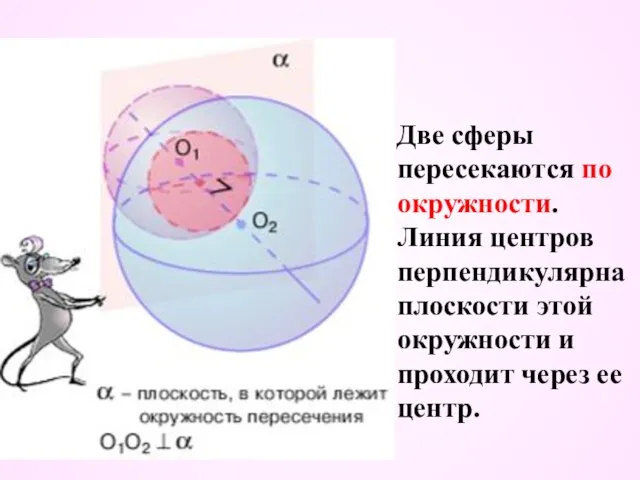
- 30. Две сферы пересекаются по окружности. Линия центров перпендикулярна плоскости этой окружности и проходит через ее центр.
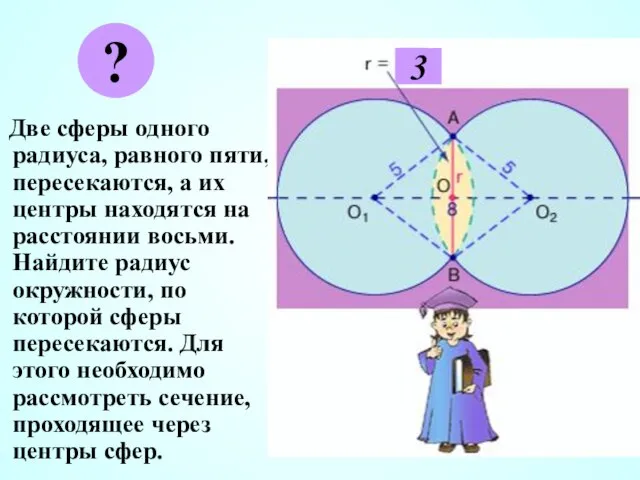
- 31. Две сферы одного радиуса, равного пяти, пересекаются, а их центры находятся на расстоянии восьми. Найдите радиус
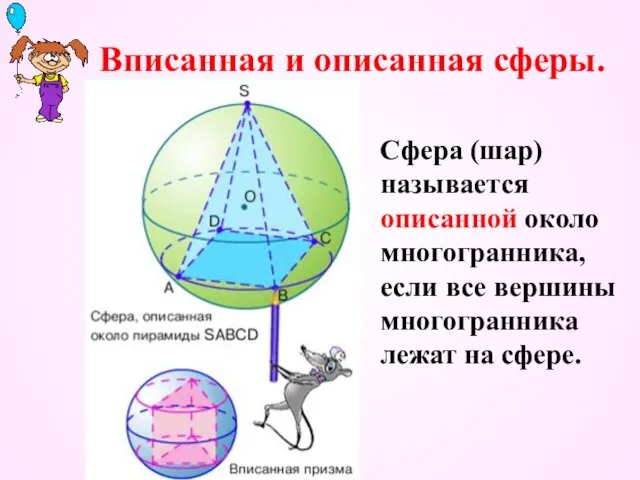
- 32. Вписанная и описанная сферы. Сфера (шар) называется описанной около многогранника, если все вершины многогранника лежат на
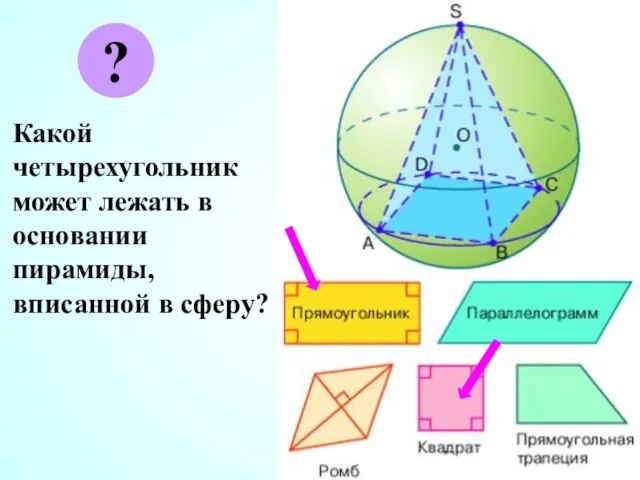
- 33. Какой четырехугольник может лежать в основании пирамиды, вписанной в сферу? ?
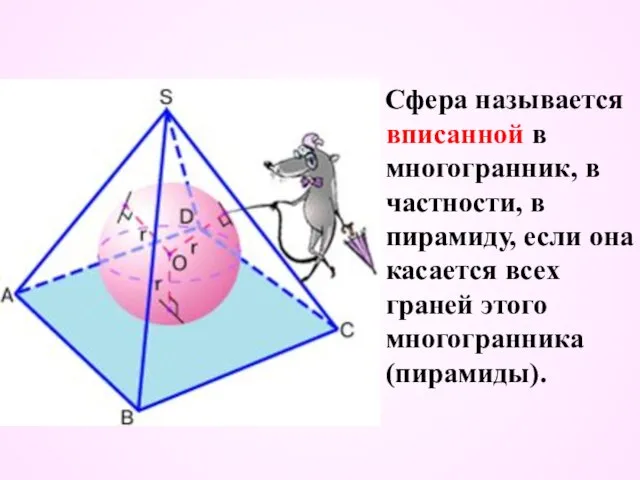
- 34. Сфера называется вписанной в многогранник, в частности, в пирамиду, если она касается всех граней этого многогранника
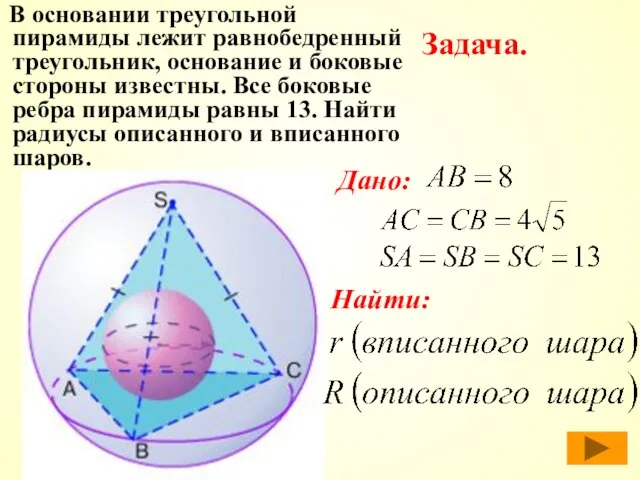
- 35. В основании треугольной пирамиды лежит равнобедренный треугольник, основание и боковые стороны известны. Все боковые ребра пирамиды
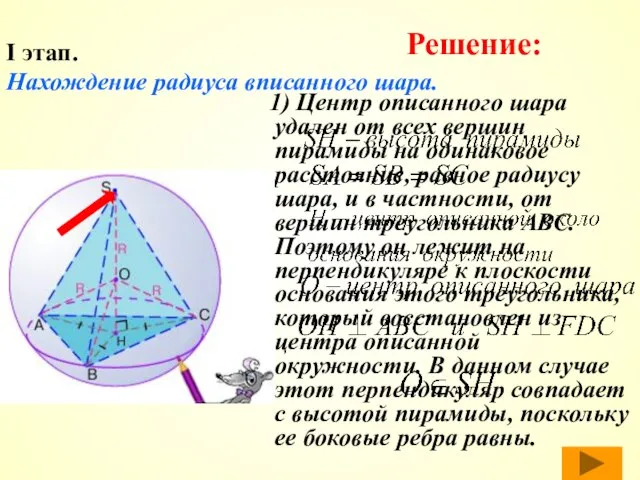
- 36. I этап. Нахождение радиуса вписанного шара. 1) Центр описанного шара удален от всех вершин пирамиды на
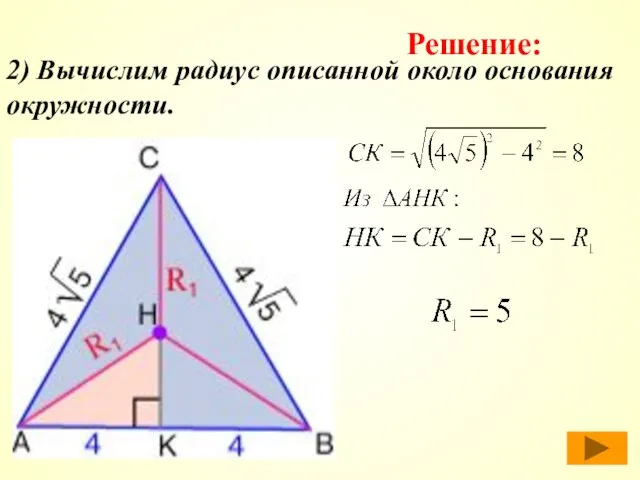
- 37. 2) Вычислим радиус описанной около основания окружности. Решение:
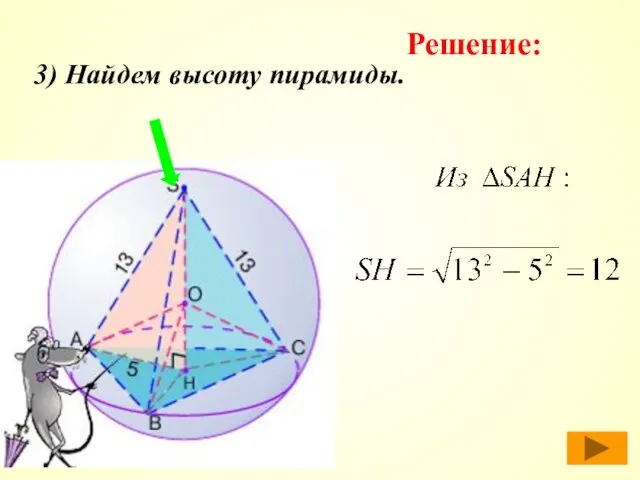
- 38. 3) Найдем высоту пирамиды. Решение:
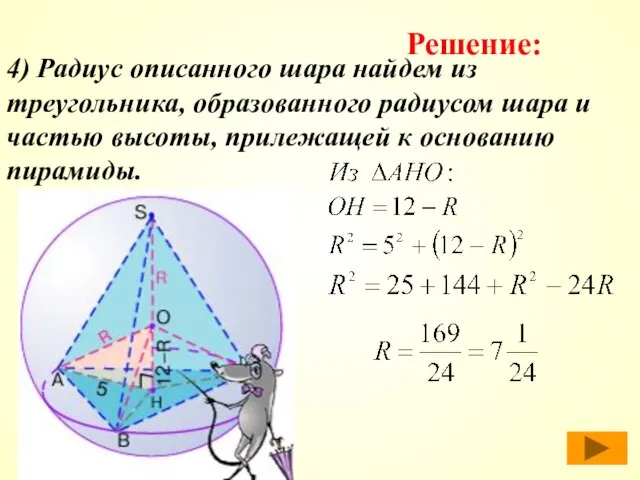
- 39. 4) Радиус описанного шара найдем из треугольника, образованного радиусом шара и частью высоты, прилежащей к основанию
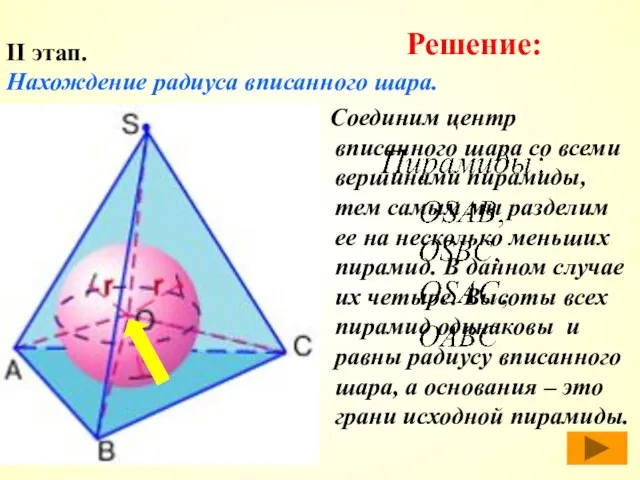
- 40. Соединим центр вписанного шара со всеми вершинами пирамиды, тем самым мы разделим ее на несколько меньших
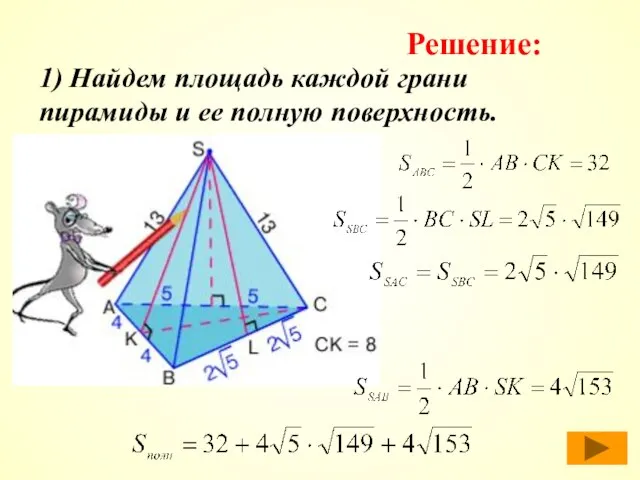
- 41. 1) Найдем площадь каждой грани пирамиды и ее полную поверхность. Решение:
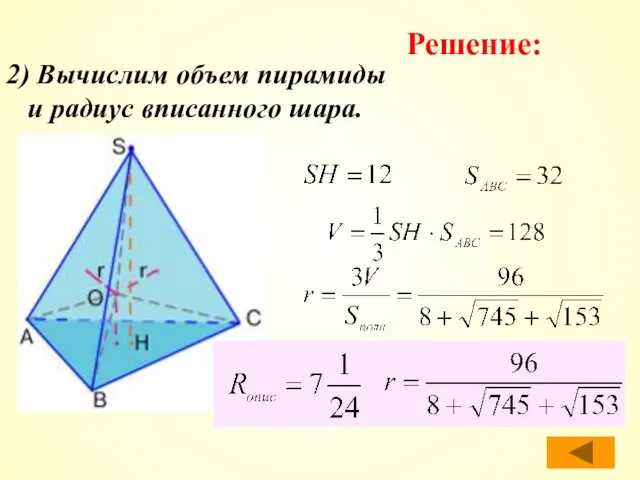
- 42. 2) Вычислим объем пирамиды и радиус вписанного шара. Решение:
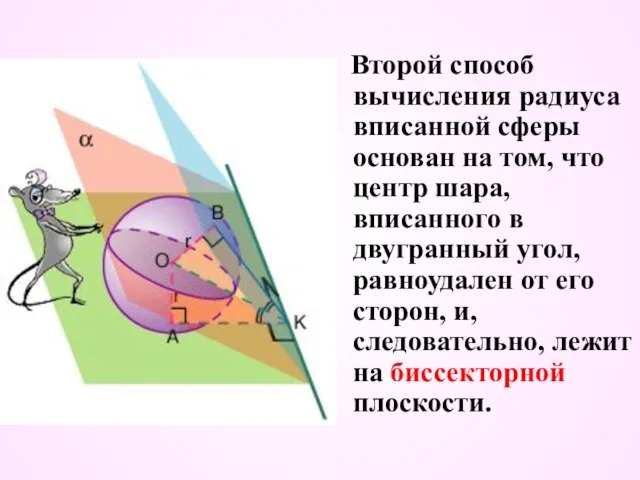
- 43. Второй способ вычисления радиуса вписанной сферы основан на том, что центр шара, вписанного в двугранный угол,
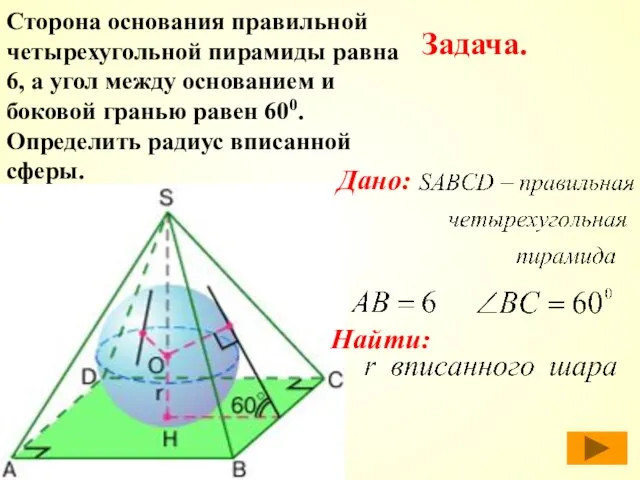
- 44. Сторона основания правильной четырехугольной пирамиды равна 6, а угол между основанием и боковой гранью равен 600.
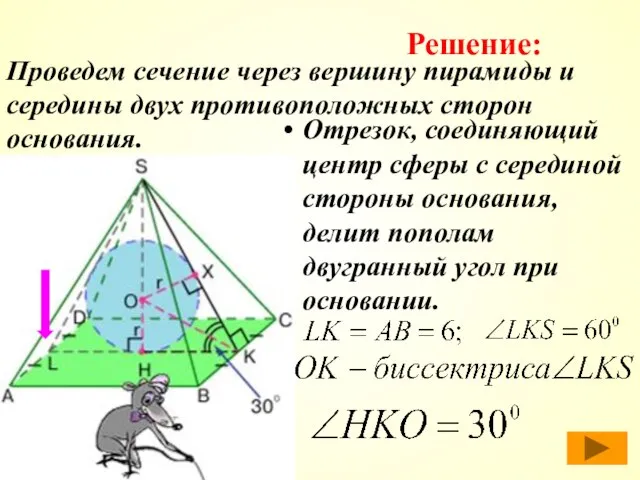
- 45. Проведем сечение через вершину пирамиды и середины двух противоположных сторон основания. Отрезок, соединяющий центр сферы с
- 47. Скачать презентацию




 Международный Юридический институт приглашает всех желающих на День Открытых дверей!
Международный Юридический институт приглашает всех желающих на День Открытых дверей! «Ожившие страницы русской истории в картинах художника Василия Сурикова»
«Ожившие страницы русской истории в картинах художника Василия Сурикова» Теоретические основы налогообложения
Теоретические основы налогообложения Отделение современной гитары. Школа МЭШДОМ, г. Калуга
Отделение современной гитары. Школа МЭШДОМ, г. Калуга Фотокросс Добру откроются сердца
Фотокросс Добру откроются сердца Современные методы и средства производства СТЭ. Лекция 1. Методология производства СТЭ
Современные методы и средства производства СТЭ. Лекция 1. Методология производства СТЭ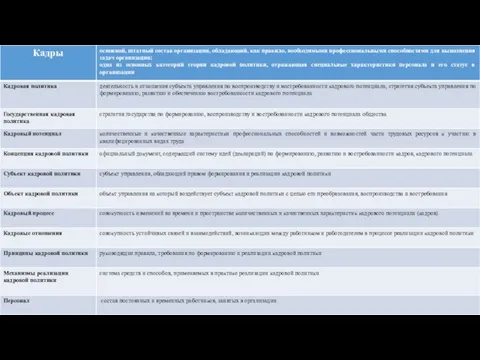 Кадровая политика. Основные термины
Кадровая политика. Основные термины Строение и работа мышц
Строение и работа мышц Presentation Title Here Subtitle
Presentation Title Here Subtitle  Как животные защищаются
Как животные защищаются Способы вальцовки и развальцовки труб
Способы вальцовки и развальцовки труб Happy Birthday Chevrolet!!!
Happy Birthday Chevrolet!!! Intel. Історія успіху
Intel. Історія успіху студсовет
студсовет Презентация на тему Профилактика ОРВИ гриппа
Презентация на тему Профилактика ОРВИ гриппа XXVI-ая Межвузовская научнопрактическая конференция молодых ученых и студентов г. Волжского
XXVI-ая Межвузовская научнопрактическая конференция молодых ученых и студентов г. Волжского Что учитывать при перепланировке
Что учитывать при перепланировке Анализ работы кафедры общественных и гуманитарных наукза 2010 – 2011 учебный год
Анализ работы кафедры общественных и гуманитарных наукза 2010 – 2011 учебный год Презентация на тему КОНСТАНТИН ГЕОРГИЕВИЧ ПАУСТОВСКИЙ
Презентация на тему КОНСТАНТИН ГЕОРГИЕВИЧ ПАУСТОВСКИЙ  Элективные курсы для предпрофильной подготовки учащихся 9-го класса по математике
Элективные курсы для предпрофильной подготовки учащихся 9-го класса по математике Золотая осень. Рисунок осеннего дерева с натуры и по памяти
Золотая осень. Рисунок осеннего дерева с натуры и по памяти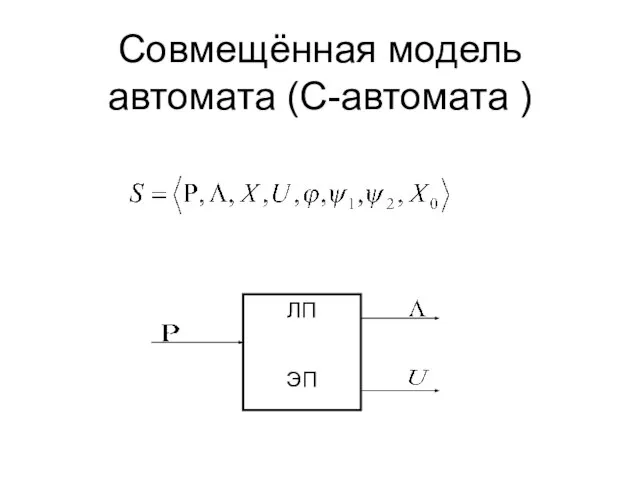 Структурный синтез C-автомата
Структурный синтез C-автомата Программное создание web-фрагментов, ускорителей и средств визуального поиска
Программное создание web-фрагментов, ускорителей и средств визуального поиска МОУ «Ракитянская средняя общеобразовательная школа № 2»
МОУ «Ракитянская средняя общеобразовательная школа № 2» Диаграммы
Диаграммы Շառլ Ազնավուր
Շառլ Ազնավուր Лигнвистическая сказка как средство преодоления трудностей при изучении морфологии русского языка
Лигнвистическая сказка как средство преодоления трудностей при изучении морфологии русского языка Возникновение института праздного класса
Возникновение института праздного класса