Содержание
- 2. §§ Волновая функция (ВФ) 02 Состояние частицы описывается волной A – амплитуда волны ω – частота
- 3. §§ Уравнение Шредингера Для частицы: Связь энергии и импульса Найдем E и P2 из волновой функции
- 4. 04 одномерное уравнение Шредингера для свободной частицы
- 5. 05 Пусть Тогда получаем УШ для стационарных состояний свободной частицы
- 6. §§ Частица в силовом поле Пусть U(x) – потенциальная энергия частицы в стационарном СП, тогда –
- 7. 07 – вероятность обнаружения частицы в интервале [x, x+dx]. Во всем пространстве то необходимо ввести нормировку.
- 8. 08 Пример: дифракция электронов Перемещая детектор можно построить график плотности вероятности обнаружения электронов |ψ2| Саму волновую
- 9. 09 Пример 2: интерференция электронов
- 10. 10 §§ Свойства УШ и решения Явления, в которых постоянная h играет существенную роль, называют квантовыми.
- 11. 11 1) E > U 2) E
- 12. 12 Если U(x) – сложная функция или содержит несколько областей, то на решение (т.е. на ψ(x))
- 13. 13 существует только при определенных значениях E = {E1, E2, … , EN, …}, а функции
- 14. §§ Потенциальные барьеры 14 Рассмотрим частицу с энергией E, которая проходит через границу двумя значениями потенциала
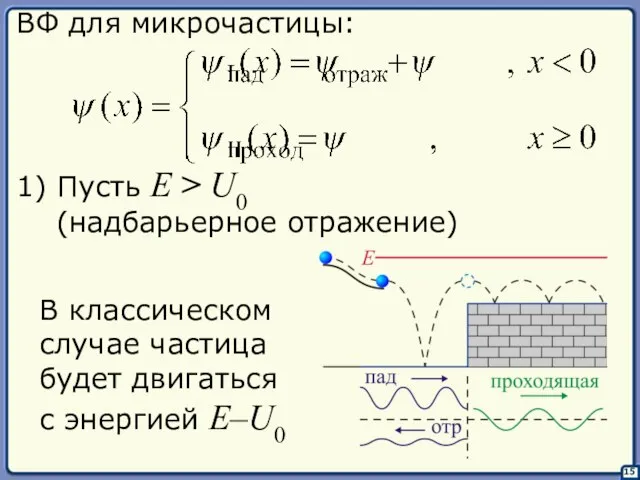
- 15. 15 ВФ для микрочастицы: 1) Пусть E > U0 (надбарьерное отражение) В классическом случае частица будет
- 16. 16 Амплитуды падающей и отраженной волны находятся из условий непрерывности и однозначности ВФ:
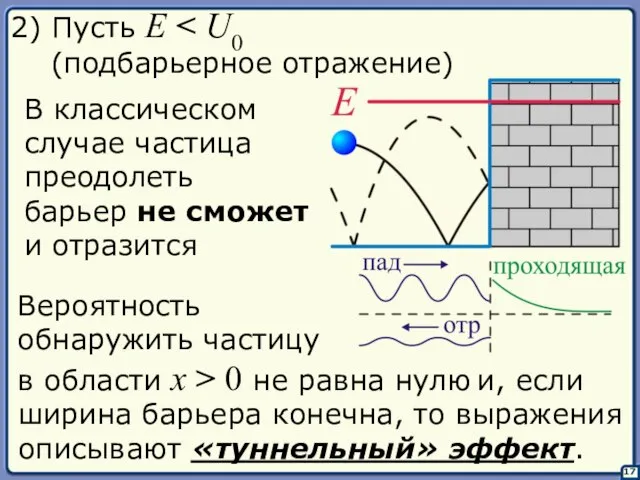
- 17. 17 В классическом случае частица преодолеть барьер не сможет и отразится Вероятность обнаружить частицу в области
- 18. §§ Потенциальная яма 18 U(x) – зависимость потенциальной энергии, которая известна с точностью до произвольной постоянной
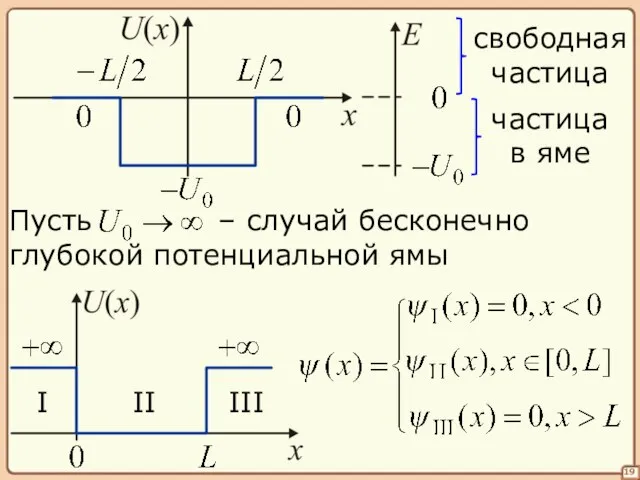
- 19. – случай бесконечно глубокой потенциальной ямы 19 свободная частица частица в яме I II III
- 20. 20 граничные условия: т.е. решение задачи возможно только при определенных значениях n.
- 21. 21 собственные значения энергии Собственные функции должны удовлетворять условию нормировки:
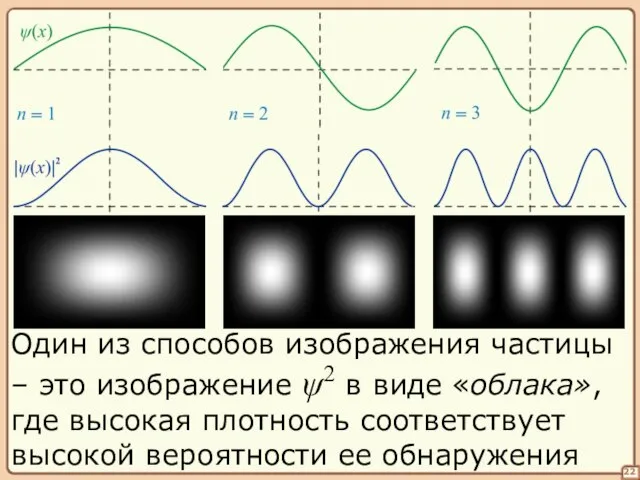
- 22. 22 Один из способов изображения частицы – это изображение ψ2 в виде «облака», где высокая плотность
- 23. 23 Выводы: 1) у связанной частицы не может быть состояния с E = 0. 2) движение
- 24. §§ Атом водорода 24 Рассмотрим атом с порядковым номером Z, который имеет 1 электрон (H,He+,Li++) Потенциал
- 25. 25 Спектр собственных значений энергии Собственные функции электрона: уравнения Шредингера: УШ решают в сферической СК
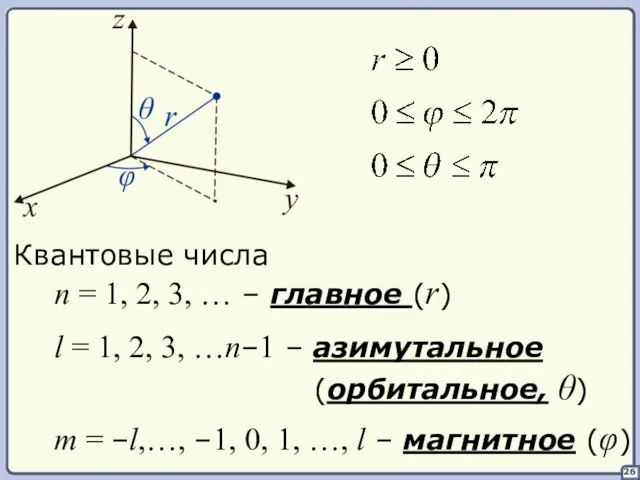
- 26. 26 Квантовые числа n = 1, 2, 3, … – главное (r) l = 1, 2,
- 27. 27 Каждому значению En соответствует несколько волновых функций с разными l и m, Такие состояния называются
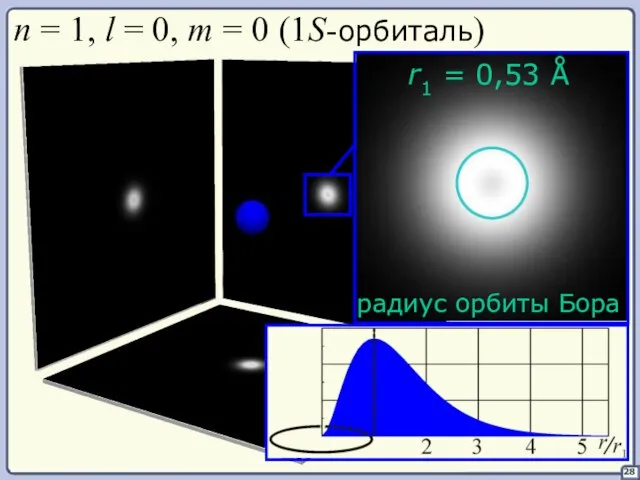
- 28. 28 n = 1, l = 0, m = 0 (1S-орбиталь)
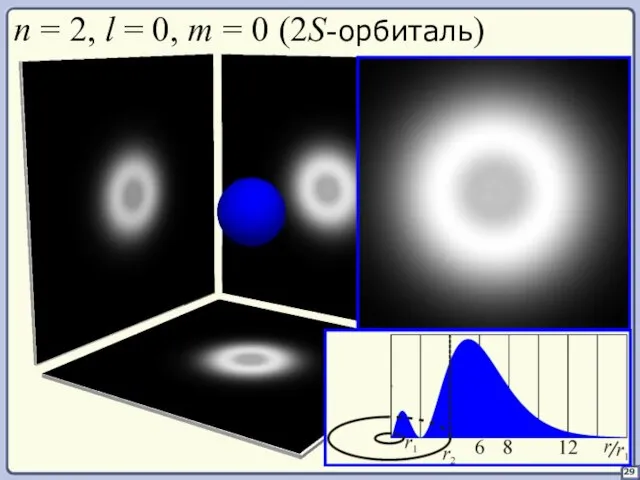
- 29. 29 n = 2, l = 0, m = 0 (2S-орбиталь)
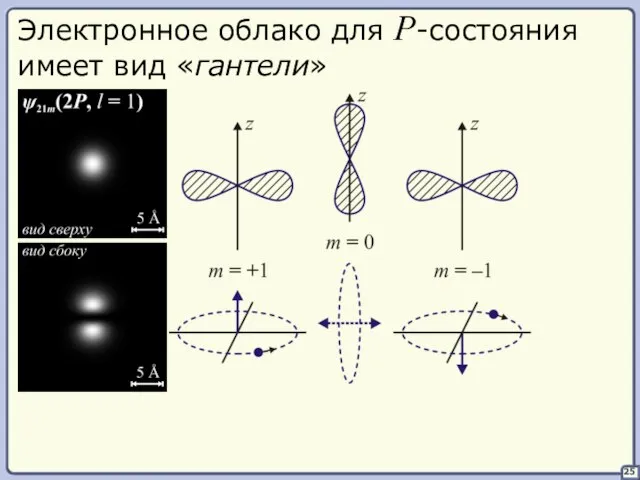
- 30. n = 2, l = 1, m = 0 (2P-орбиталь) n = 2, l = 1,
- 31. 31 Электронное облако для S-состояния имеет шаровую симметрию с характерным радиусом 0,5(S1)–5Å(S3).
- 32. 25 Электронное облако для P-состояния имеет вид «гантели»
- 33. §§ Правило отбора Переходы электрона между уровнями возможны только с Δl = ±1. Фотон изменяет момент
- 34. §§ Многоэлектронные атомы 34 Атом с порядковым номером Z содержит Z электронов, которые двигаются в поле
- 35. 35 К тройке добавим еще одно квантовое число. Электрон обладает спином – внутренним (собственным) моментом количества
- 36. 36 Принцип (запрета) Паули В квантовой системе (атоме) Иными словами, в одном и том же состоянии
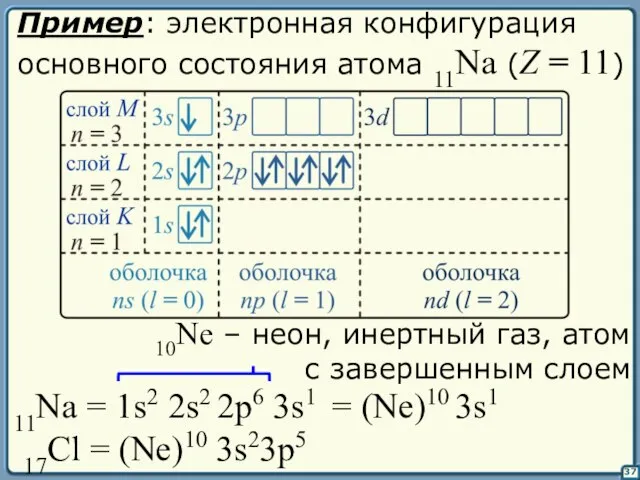
- 37. 37 Пример: электронная конфигурация основного состояния атома 11Na (Z = 11) 11Na = 1s2 2s2 2p6
- 38. 38 §§ Энергетические зоны Описание системы взаимодействующих электронов и ядер связано с расчетными и математическими трудностями.
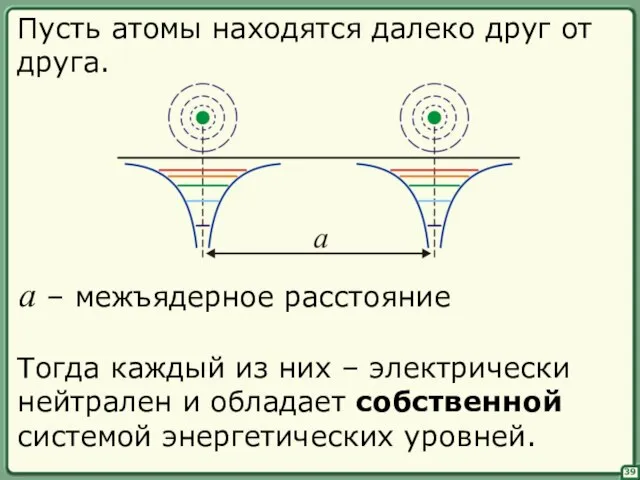
- 39. 39 Тогда каждый из них – электрически нейтрален и обладает собственной системой энергетических уровней. Пусть атомы
- 40. 40 На малом расстоянии электронные уровни смещаются из-за действия поля соседних атомов, при этом снимается вырождение
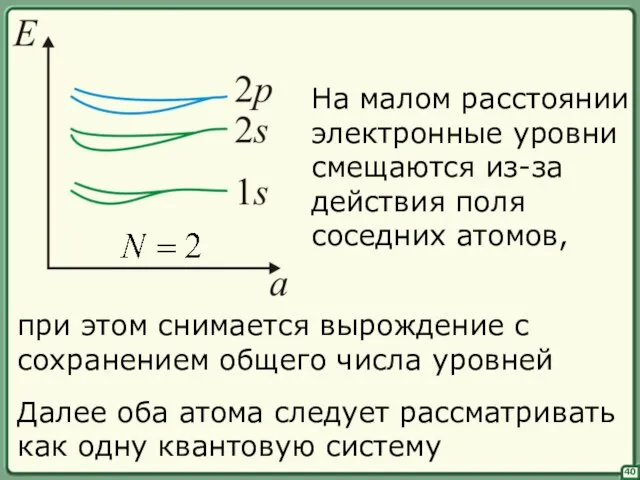
- 41. 41 Рассмотрим твердое тело (N = ∞) Совокупность большого числа уровней образует энергетические зоны разрешенные –
- 42. 42 При заполнении разрешенных зон принцип запрета остается справедливым При T = 0 заполняются сначала уровни
- 43. 43 Электроны полностью заполненных энергетических зон не участвуют в процессах переноса При ΔE ≥ 5 эВ
- 44. 44 Энергетическая схема для проводника. Электроны частично заполненной зоны участвуют в процессах переноса Энергетическая структура реального
- 45. 45 §§ Вынужденное излучение Вероятность заселения уровня определяется законом Больцмана При термодинамическом равновесии число частиц на
- 46. 46 Если атом переходит с уровня Em на уровень En, то произойдет излучение кванта с энергией
- 47. 47 Если система находится в состоянии равновесия, то она будет поглощать проходящее через нее излучение При
- 48. 48 Схема лазера оптического квантового генератора Многократно отразившись от зеркал резонатора из лазера выходит свет, обладающий
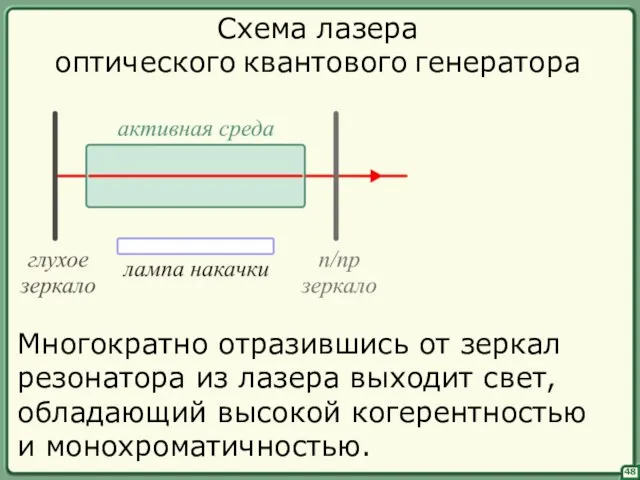
- 49. 49 §§ Типы лазеров Лазеры классифицируют по агрегатному состоянию рабочего тела: 1) твердотельные 2) газовые 3)
- 50. – корунд (Al2O3), кристалл, примесь – Cr (хром) – стекло, аморфное тело, примесь – Nd (неодим)
- 51. 51 Газовые лазеры: 1) атомарные – лазеры на инертных газах (He, Ne, Ar, Kr, He-Ne) 2)
- 52. 52 Жидкостные лазеры имеют в качестве рабочего тела неорганическую жидкость или раствор органических красителей Используется оптическая
- 54. Скачать презентацию





![07 – вероятность обнаружения частицы в интервале [x, x+dx]. Во всем пространстве то необходимо ввести нормировку.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/278868/slide-6.jpg)



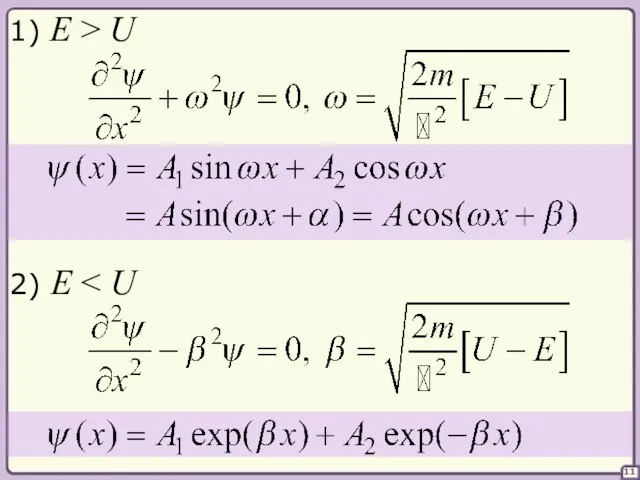





























 Висит за окошком Кулёк ледяной, Он полон капели И пахнет весной
Висит за окошком Кулёк ледяной, Он полон капели И пахнет весной Средства регулирования движением поездов
Средства регулирования движением поездов Афины при Перикле
Афины при Перикле Электронная таблица EXCEL
Электронная таблица EXCEL Архетипы
Архетипы УНИДРУА: международный институт по унификации частного права
УНИДРУА: международный институт по унификации частного права Органы чувств
Органы чувств  «Этимологический анализ прозвищ жителей деревень Завражье, Мешково и поселка Судоверфь Судоверфского сельского поселения»
«Этимологический анализ прозвищ жителей деревень Завражье, Мешково и поселка Судоверфь Судоверфского сельского поселения» Новогодние открытки
Новогодние открытки Робототехника. Проект
Робототехника. Проект Балансирующий рынок
Балансирующий рынок Теорема Пифагора
Теорема Пифагора Культура XX века
Культура XX века Деревня Юрьевец
Деревня Юрьевец Wine. The benefits of wine with moderate consumption
Wine. The benefits of wine with moderate consumption Биопсихосоциодуховный подход к профилактике профессионального выгорания психологов
Биопсихосоциодуховный подход к профилактике профессионального выгорания психологов Воздействие высокоскоростных магистралей на окружающую среду
Воздействие высокоскоростных магистралей на окружающую среду Презентация экскурсии в животноводческий комплекс «ИП Каюмов»
Презентация экскурсии в животноводческий комплекс «ИП Каюмов» 07_0___163
07_0___163 каждую неделю около 600 000 слушателей включаются на частоту 100,5 FM каждый день Радио BEST FM слушают около 300 000 человек каждые 15 минут на в
каждую неделю около 600 000 слушателей включаются на частоту 100,5 FM каждый день Радио BEST FM слушают около 300 000 человек каждые 15 минут на в «Белые» в Гражданской войне
«Белые» в Гражданской войне Внедрение здоровьесберегающих технологий
Внедрение здоровьесберегающих технологий Русское искусство 2 пол.19 века
Русское искусство 2 пол.19 века Всегда ли правы мы- родители?
Всегда ли правы мы- родители? Итоги работы отрасли в 2010 году и задачи на 2011 год Глава департамента Елена Борисовна Чеснокова
Итоги работы отрасли в 2010 году и задачи на 2011 год Глава департамента Елена Борисовна Чеснокова Семейные традиции семьи Митрофановых
Семейные традиции семьи Митрофановых HADI – это экспериментальный научный метод исследования, переложенный на бизнес
HADI – это экспериментальный научный метод исследования, переложенный на бизнес ПРОЕКТ КНИЖКА-САМОДЕЛКА «Волшебница Зима» 4 класс
ПРОЕКТ КНИЖКА-САМОДЕЛКА «Волшебница Зима» 4 класс