Презентация на тему Вычисление объема цилиндра

Устные упражнения по теме.
Решение стереометрических задач.
Выполнение практической работы.
Самостоятельная работа.
План урока

Чтобы избегать ошибок, надо набираться опыта; чтобы набираться опыта, надо делать ошибки
/А.Н. Колмогоров/
(1903-1987)

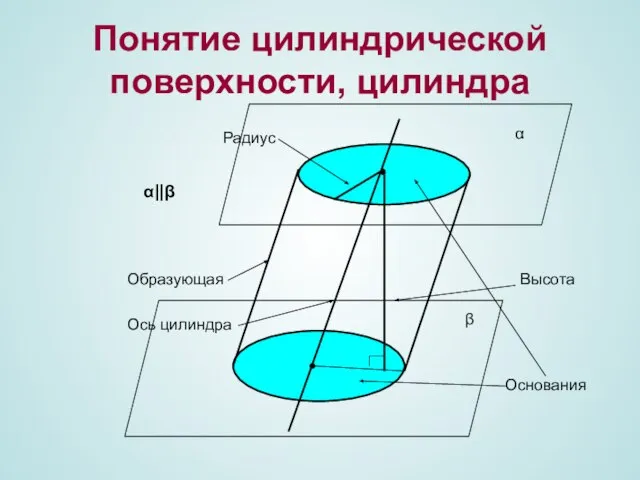
Понятие цилиндрической поверхности, цилиндра

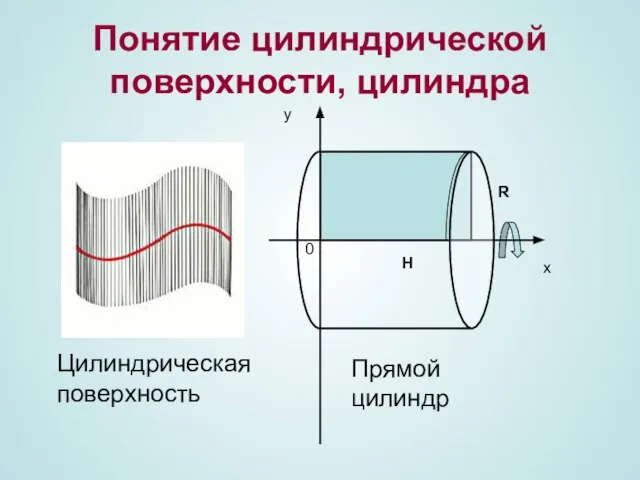
Понятие цилиндрической поверхности, цилиндра
х
у
0
Н
R
Прямой цилиндр
Цилиндрическая
поверхность

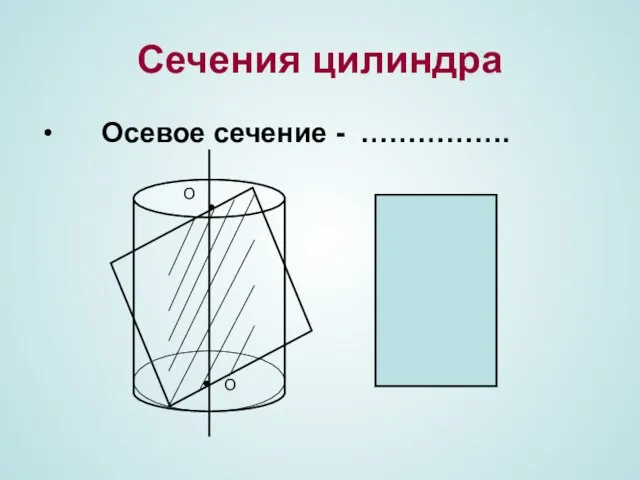
Сечения цилиндра
Осевое сечение - …………….
О
О

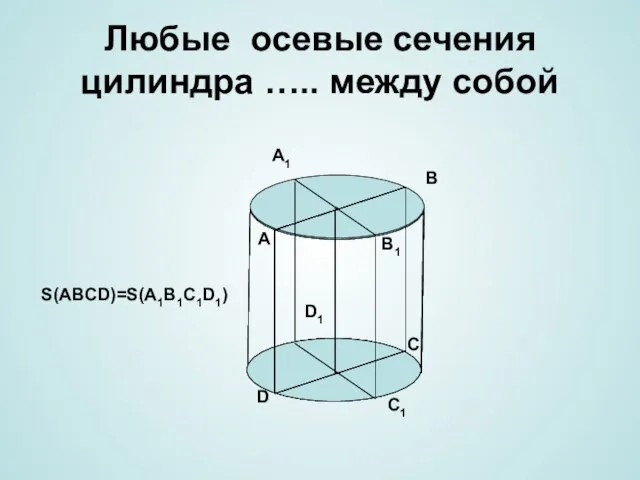
Любые осевые сечения цилиндра ….. между собой
A
B
C
D
A1
B1
C1
D1
S(ABCD)=S(A1B1C1D1)

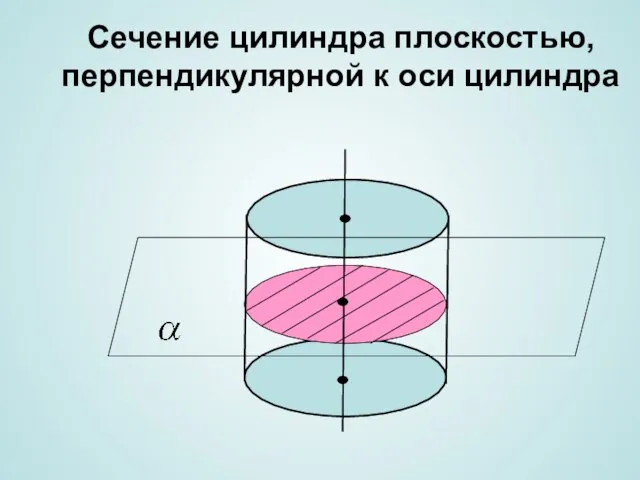
Сечение цилиндра плоскостью, перпендикулярной к оси цилиндра

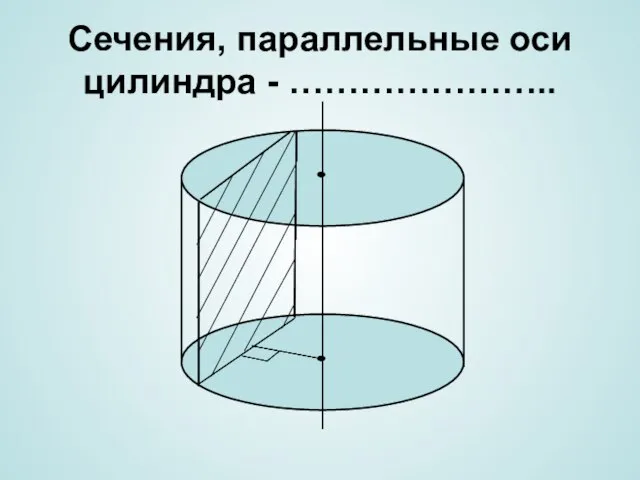
Сечения, параллельные оси цилиндра - …………………..

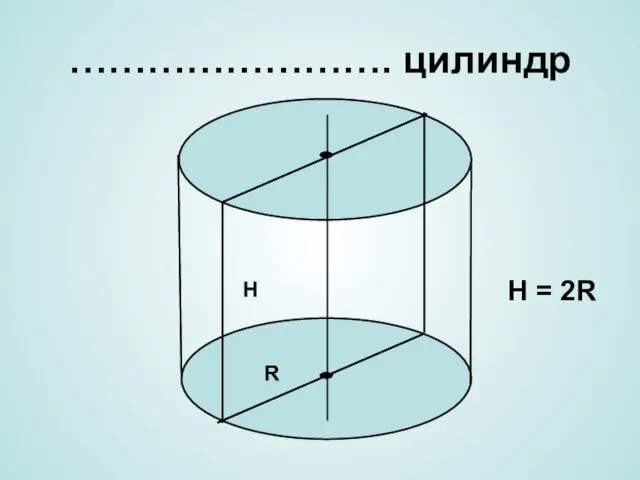
……………………. цилиндр
H
R
H = 2R

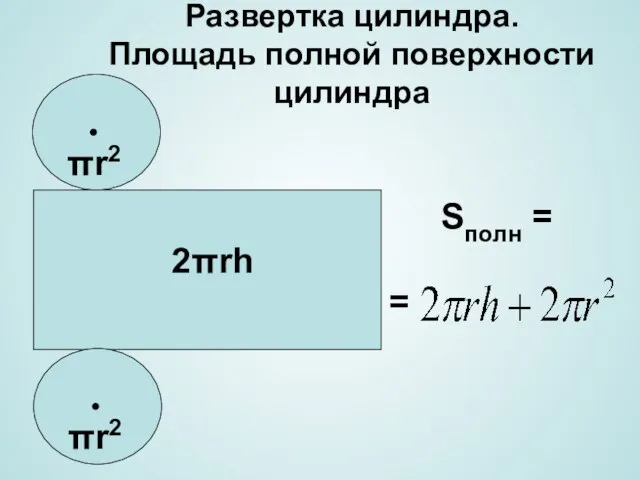
Развертка цилиндра.
Площадь полной поверхности цилиндра
Sполн =
=
πr2
πr2
2πrh

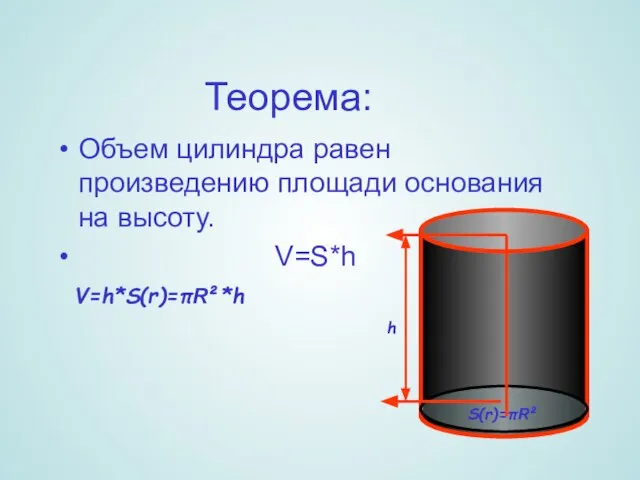
Теорема:
Объем цилиндра равен произведению площади основания на высоту.
V=S*h
V=h*S(r)=πR²*h
S(r)=πR²
h

Решение стереометрических задач

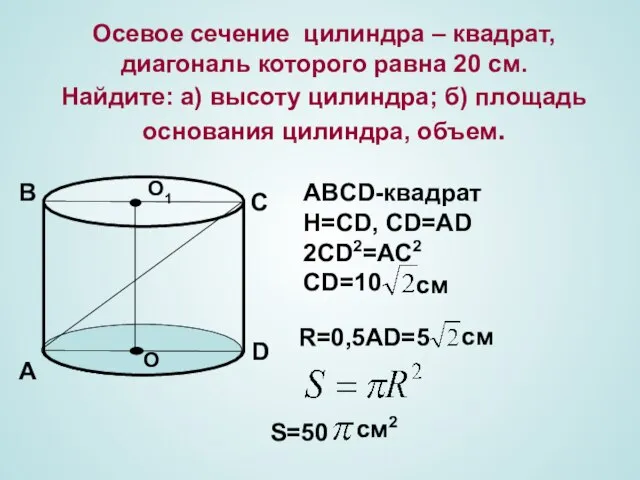
Осевое сечение цилиндра – квадрат, диагональ которого равна 20 см.
Найдите: а) высоту цилиндра; б) площадь основания цилиндра, объем.
О
О1
А
В
С
D
ABCD-квадрат
Н=СD, CD=AD
2CD2=AC2
CD=10
см
R=0,5AD=5
см
S=50
см2

Площадь осевого сечения цилиндра равна
10 м2, а площадь основания равна 5 м2.
Найдите высоту цилиндра, объем.
А
В
С
D
O
O1
R
H
R=
H=
м

1. Верно ли, что образующая цилиндра больше его высоты?
Самостоятельная работа
2. Может ли площадь боковой поверхности цилиндра быть
равной площади его осевого сечения?
3. Назовите плоскую фигуру, при вращении которой вокруг
одной из сторон образуются цилиндр.
4. Может ли развёртка боковой поверхности цилиндра
быть квадратом?
5. Верно ли, что среди всех сечений цилиндра, проходящих
через его образующие, наибольшую площадь имеет
осевое сечение?

Какая фигура получается в сечении цилиндра
плоскостью, проходящей перпендикулярно оси
цилиндра?
Круг
Какая фигура получается в сечении цилиндра
плоскостью, проходящей через ось цилиндра?
Прямоугольник
Чему равна площадь осевого сечения
равностороннего цилиндра, высота
которого равна 6 см?
36 см2

Задание 1. Произведя необходимые измерения, вычислите:
? площадь боковой поверхности цилиндра;
? площадь полной поверхности цилиндра;
? объем цилиндра.
Выполнение практической работы
Задание 2. Увеличьте радиус в два раза, высоту уменьшите в три раза и найдите те же величины.
Проверка

Знания, в противоположность вещам, обладают неограниченной способностью к накоплению.
/Аристотель/
(384 до н. э.(384 до н. э.) — древнегреческий(384 до н. э.) — древнегреческий философ(384 до н. э.) — древнегреческий философ и учёный.