Содержание
Слайд 2ЗАДАЧА №7(СТР.8).
Две прямые пересекаются в точке М. Докажите, что все прямые, не
ЗАДАЧА №7(СТР.8).
Две прямые пересекаются в точке М. Докажите, что все прямые, не

проходящие через точку М и пересекающие данные прямые, лежат в одной плоскости. Лежат ли в одной плоскости все прямые, проходящие через точку М?
Слайд 3 М
а
b
Дано: а,b-прямые;
M-точка пересечения прямых;
Доказать: 1) Прямые, пересекающие прямые a,b,
М
а
b
Дано: а,b-прямые;
M-точка пересечения прямых;
Доказать: 1) Прямые, пересекающие прямые a,b,

лежат в одной плоскости.
2) Прямые, пересекающие точку М, лежат в одной плоскости.
2) Прямые, пересекающие точку М, лежат в одной плоскости.
ДОКАЗАТЕЛЬСТВО.
1)Отметим на прямой а некоторую точку K. По первому следствию через точку K и прямую b проходит плоскость α, но так как точка М является точкой прямой а, то по второй аксиоме и прямая а лежит в плоскости α. Так как прямые a,b лежат в плоскости α, то все прямые, проходящие через них будут иметь 2 общих точки с плоскостью, то есть лежать в данной плоскости.
2)Прямые, проходящие через точку М, не будут лежать в плоскости α, так как по второй аксиоме в плоскости должно лежать минимум две точки прямой.
Ответ: 1)Да 2)Нет.
α
K
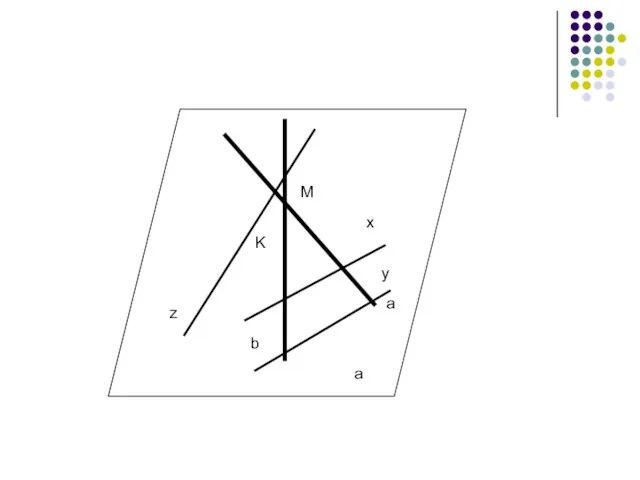
Слайд 4M
a
b
K
a
z
x
y
M
a
b
K
a
z
x
y
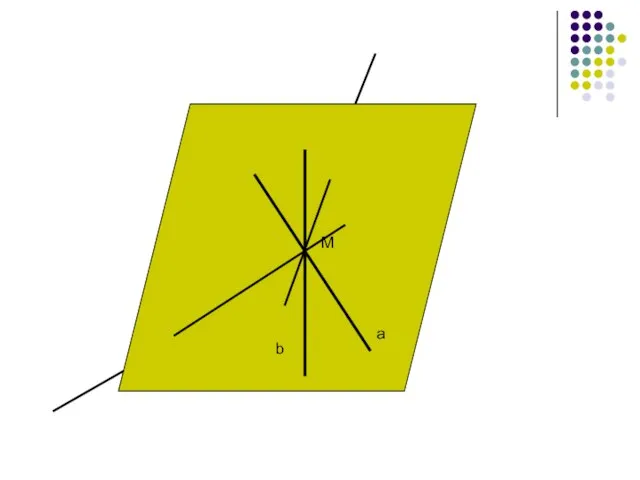
Слайд 5
M
a
b
M
a
b
- Предыдущая
Презентация к уроку геометриив 7 классеСледующая -
Реши примеры МАРКЕТИНГ
МАРКЕТИНГ Химия в медицине
Химия в медицине 0006d06c-2b7ab0fb
0006d06c-2b7ab0fb Орёл на горе, перо на орле.Гора под орлом,орёл под пером.
Орёл на горе, перо на орле.Гора под орлом,орёл под пером. Citation One бриф (002)
Citation One бриф (002) Средняя линия трапеции
Средняя линия трапеции Транспортные запасы
Транспортные запасы Архитектура и дизайн
Архитектура и дизайн Презентация на тему Политическая мысль древнего востока
Презентация на тему Политическая мысль древнего востока  Prezentatsia___po_Istorii_Uratkina_Mikhaila____4
Prezentatsia___po_Istorii_Uratkina_Mikhaila____4 Материнские платы
Материнские платы Click to edit Master title style Click to edit Master subtitle style
Click to edit Master title style Click to edit Master subtitle style  - программастратегического назначения
- программастратегического назначения Аз, буки, веди (из истории русского алфавита)
Аз, буки, веди (из истории русского алфавита) Презентация на тему БИОЛОГИЯ РАСТЕНИЯ
Презентация на тему БИОЛОГИЯ РАСТЕНИЯ  Презентация на тему Гравитация
Презентация на тему Гравитация Презентация на тему Welcome to Australia
Презентация на тему Welcome to Australia  Презентация школьной библиотеки
Презентация школьной библиотеки The National Parks in Great Britain
The National Parks in Great Britain Традиции, парадигмы и споры в теории международных отношений
Традиции, парадигмы и споры в теории международных отношений Применение механизма Совместного Осуществления Киотского Протокола для организации финансирования проекта по использованию др
Применение механизма Совместного Осуществления Киотского Протокола для организации финансирования проекта по использованию др Театральный коллектив Маски
Театральный коллектив Маски Биография Чарльза Дарвина
Биография Чарльза Дарвина Аппликация «Собачка»
Аппликация «Собачка» Пираньи. Речные монстры
Пираньи. Речные монстры Понятие информации, 10 кл. Семакин ФГОС
Понятие информации, 10 кл. Семакин ФГОС АвтоВАЗ. История завода
АвтоВАЗ. История завода Становись партнером и зарабатывай с продажи билетов
Становись партнером и зарабатывай с продажи билетов