Слайд 2 « Геометрия обладает двумя великими сокровищами. Первое - это теорема Пифагора,

которую можно сравнить
с мерой золота…»
И. Кеплер
Слайд 3Цель:
внимательно изучив формулировку теоремы Пифагора, проанализировав доказательство и используя обобщение, предложить

более широкий круг объектов, при помощи которых происходит доказательство теоремы Пифагора, создав тем самым новую интерпретацию её формулировки.
Задачи:
1) обобщение материала по исследуемой теме. 2) применение теоремы Паппа как дополнительного инструмента проекта.
3) систематизирование информации, представленной в проекте.
4) создание новой интерпретации формулировки теоремы Пифагора.
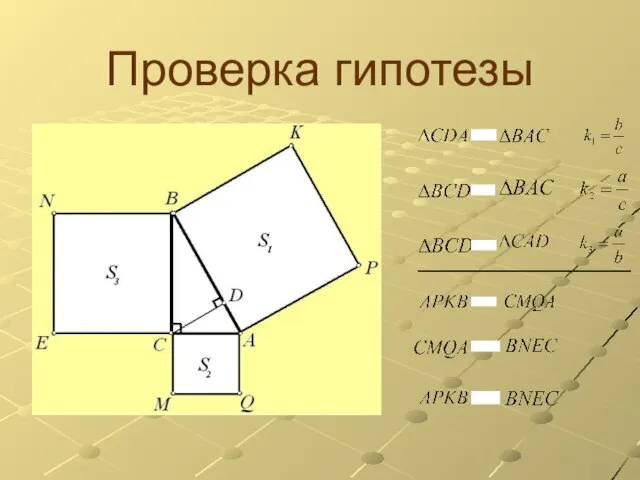
Слайд 4 ГИПОТЕЗА
Если я (в доказательстве теоремы Пифагора) на сторонах прямоугольного треугольника

построю не квадраты (как предложил Пифагор), а подобные многоугольники, то будет ли справедливо, что площадь многоугольника, построенного на гипотенузе, равна сумме площадей многоугольников, построенных на катетах? Если я это докажу, то у меня появится новая интерпретация формулировки теоремы Пифагора, что обогатит задачный материал, а главное, будет иметь интересное обобщение.
Слайд 5 Теорема Паппа
Если на сторонах произвольного треугольника АВС построить параллелограммы соответствующим образом,

то площадь параллелограмма, построенного на большей стороне, равна сумме площадей двух остальных.
Слайд 7 На сторонах прямоугольного треугольника построим равносторонние треугольники. Достроив их до параллелограммов
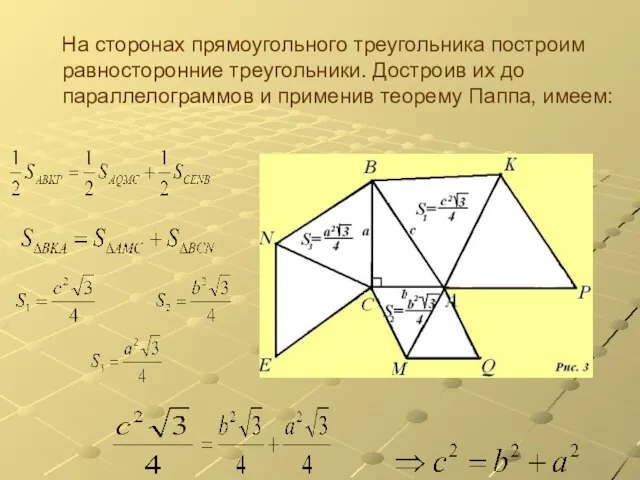
и применив теорему Паппа, имеем:
Слайд 8 На сторонах прямоугольного треугольника построим равнобедренные подобные треугольники.
Достроив их до
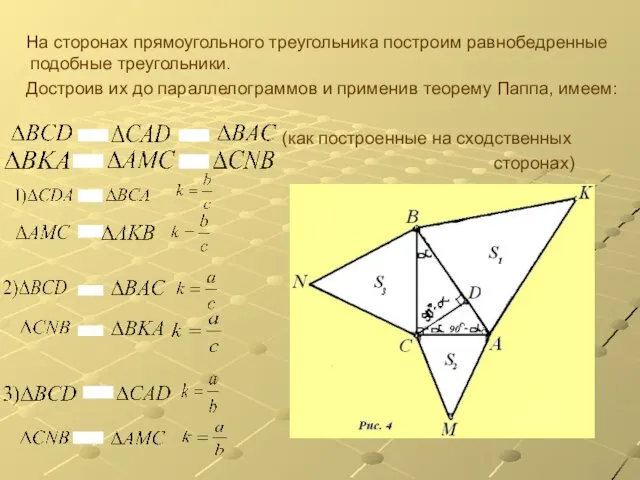
параллелограммов и применив теорему Паппа, имеем:
(как построенные на сходственных
сторонах)
Слайд 9 На сторонах прямоугольного треугольника построим разносторонние подобные треугольники с коэффициентами подобия
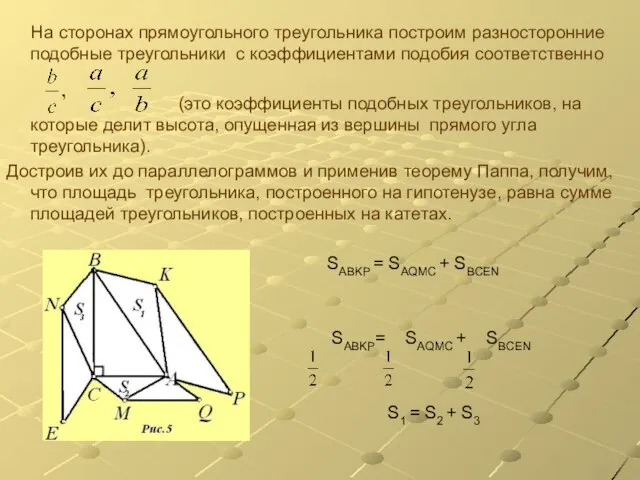
соответственно
(это коэффициенты подобных треугольников, на которые делит высота, опущенная из вершины прямого угла треугольника).
Достроив их до параллелограммов и применив теорему Паппа, получим, что площадь треугольника, построенного на гипотенузе, равна сумме площадей треугольников, построенных на катетах.
SABKP = SAQMC + SBCEN
SABKP= SAQMC + SBCEN
S1 = S2 + S3







 Повышенный доход от облигаций: продвинутый курс
Повышенный доход от облигаций: продвинутый курс Игорь Северянин (Игорь Васильевич Лотарёв) 1887-1941
Игорь Северянин (Игорь Васильевич Лотарёв) 1887-1941 Особенности социально-экономического развития ведущих стран глобальной экономики в 1870-1913
Особенности социально-экономического развития ведущих стран глобальной экономики в 1870-1913 Восстановление Арала
Восстановление Арала Гражданские правоотношения
Гражданские правоотношения Лось - лесная корова, волк - хвост палкой
Лось - лесная корова, волк - хвост палкой ОКСЮМОРОН
ОКСЮМОРОН Отражение краткосрочных активов обязательств, доходов и расходов
Отражение краткосрочных активов обязательств, доходов и расходов  BI в облачных вычислениях. SQL Azure Reporting
BI в облачных вычислениях. SQL Azure Reporting Интересные свойства воды
Интересные свойства воды Стили мебели (часть 2)
Стили мебели (часть 2) Московский Кремль (2 класс)
Московский Кремль (2 класс) Presentations_ZS_2022-23
Presentations_ZS_2022-23 Проект «Интересное рисование»
Проект «Интересное рисование» Презентация на тему Объёмная снежинка
Презентация на тему Объёмная снежинка Кредит в США и России
Кредит в США и России ИСС Аюдар Инфо. Информационно-справочная система для бухгалтера коммерческой организации государственного учреждения
ИСС Аюдар Инфо. Информационно-справочная система для бухгалтера коммерческой организации государственного учреждения Психологія брехні та обману
Психологія брехні та обману Уход за одеждой
Уход за одеждой Экстренная помощь в гинекологии
Экстренная помощь в гинекологии  Полевые компьютеры
Полевые компьютеры Мордовские узоры
Мордовские узоры Кавказская война
Кавказская война Орнамент: ленточный, сетчатый, композиционно-замкнутый
Орнамент: ленточный, сетчатый, композиционно-замкнутый Открытое акционерное общество «Шестая генерирующая компания оптового рынка электроэнергии» Финансовые и операционные итоги де
Открытое акционерное общество «Шестая генерирующая компания оптового рынка электроэнергии» Финансовые и операционные итоги де Династия Тургелей
Династия Тургелей Оружие нашей армии и противника в начале Великой Отечественной войны.
Оружие нашей армии и противника в начале Великой Отечественной войны. Практиканы АО Костанайский мелькомбинат
Практиканы АО Костанайский мелькомбинат