Содержание
- 2. Вопрос1 Дискретизация непрерывных сигналов Во многих случаях первичные сигналы в ТКС непрерывны как по множеству, так
- 3. Вопрос1 Дискретизация непрерывных сигналов Дискретизация по времени заключается в замене непрерывного сигнала b(t) дискретным по времени
- 4. Вопрос1 Дискретизация непрерывных сигналов Очевидно, с уменьшением интервала дискретизации воспроизводящая функция будет с большей точностью отображать
- 5. Вопрос1 Дискретизация непрерывных сигналов Частотный критерий академика В.А. Котельникова. Данный критерий выбора частоты квантования базируется на
- 6. Вопрос1 Дискретизация непрерывных сигналов Слайд 6 Рис. 2 Рис. 3
- 7. Вопрос1 Дискретизация непрерывных сигналов Слайд 7 Рис.4 Представление непрерывной функции времени с ограниченным спектром Как видно
- 8. Вопрос1 Дискретизация непрерывных сигналов
- 9. Вопрос1 Дискретизация непрерывных сигналов Слайд 9
- 10. Вопрос1 Дискретизация непрерывных сигналов Слайд 10
- 11. ВОПРОС 2 Квантование по уровню Слайд 11 Рассмотрим четыре способа описания аналоговой исходной информации. Возможные варианты
- 12. ВОПРОС 2 Квантование по уровню Даже если дискретные сигналы имеют плоские вершины, возможные значения составляют бесконечное
- 13. ВОПРОС 2 Квантование по уровню Это искажение, вызванное необходимостью аппроксимации аналогового сигнала квантованными выборками, называется шумом
- 14. ВОПРОС 2 Квантование по уровню Слайд 14 Шаг между уровнями квантования называется интервалом квантования (q). Каждое
- 15. ВОПРОС 2 Квантование по уровню Слайд 15 При этом для слабых сигналов Рш.кв уменьшается, а для
- 17. Скачать презентацию
Слайд 2Вопрос1 Дискретизация непрерывных сигналов
Во многих случаях первичные сигналы в ТКС непрерывны как
Вопрос1 Дискретизация непрерывных сигналов
Во многих случаях первичные сигналы в ТКС непрерывны как
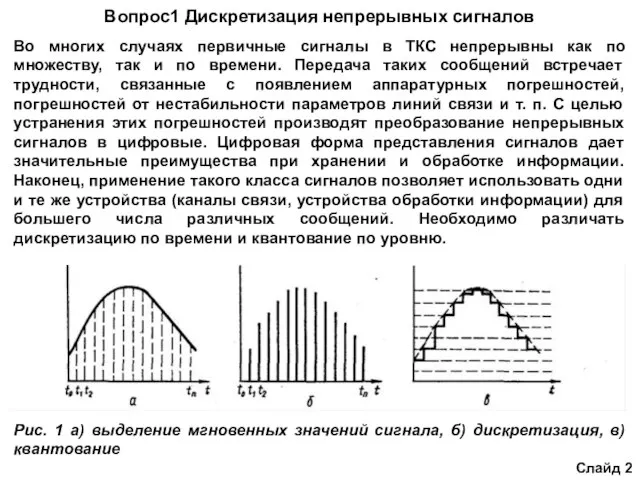
Рис. 1 а) выделение мгновенных значений сигнала, б) дискретизация, в) квантование
Слайд 2
Слайд 3Вопрос1 Дискретизация непрерывных сигналов
Дискретизация по времени заключается в замене непрерывного сигнала b(t)
Вопрос1 Дискретизация непрерывных сигналов
Дискретизация по времени заключается в замене непрерывного сигнала b(t)

При дискретизации по времени непрерывная по аргументу функция b(t), описывающая сигнал, преобразуется в функцию bд(t) дискретного аргумента. Такое преобразование может быть выполнено путем взятия отсчетов функции b(t) в определенные дискретные моменты времени t0, t1, t2, ..., tk. В результате функция b(t) заменяется совокупностью мгновенных значений b(ti), i = 0, 1, 2, ..., k.
Временной интервал между двумя соседними фиксированными моментами времени, в которых задается дискретная функция, называется интервалом дискретизации. Величина, обратная интервалу дискретизации, называется частотой дискретизации: fд=1/ . По мгновенным значениям b(ti) можно восстановить исходную функцию с определенной точностью. Функцию, полученную в результате восстановления по отсчетам b(ti), называют воспроизводящей.
Слайд 4Вопрос1 Дискретизация непрерывных сигналов
Очевидно, с уменьшением интервала дискретизации воспроизводящая функция будет с
Вопрос1 Дискретизация непрерывных сигналов
Очевидно, с уменьшением интервала дискретизации воспроизводящая функция будет с

Дискретизация сигналов по времени может быть равномерной и не-равномерной.
При равномерной дискретизации функции b(t) интервал постоянен. Его величина выбирается на основе априорных сведений о характеристиках сигнала.
При неравномерной дискретизации интервал между отсчетами изменяется по случайному закону или с учетом изменения характеристик сигнала (адаптивная дискретизация). Адаптивную дискретизацию реализовать труднее, чем равномерную, однако она позволяет значительно сократить число избыточных отсчетов.
Известно несколько критериев выбора интервалов временной дискретизации. В подавляющем большинстве случаев используется частотный критерий академика В.А. Котельникова (есть еще корреляционный критерий Н.А. Железнова, критерий отклонения воспроизводящей функции от исходной и др.)
Слайд 5Вопрос1 Дискретизация непрерывных сигналов
Частотный критерий академика В.А. Котельникова. Данный критерий выбора частоты
Вопрос1 Дискретизация непрерывных сигналов
Частотный критерий академика В.А. Котельникова. Данный критерий выбора частоты

Аналитически теорема Котельникова выражается интерполяционным рядом
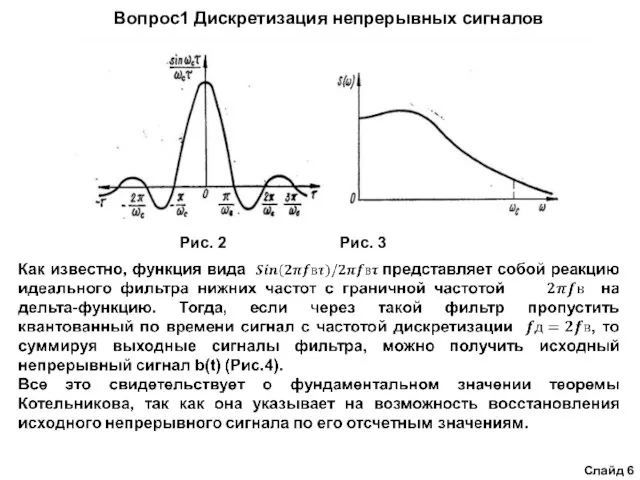
Непосредственно из этого выражения следует, что непрерывная функция с ограниченным спектром может быть представлена в виде суммы бесконечно большого числа членов, каждый из которых является произведением функции вида Sin(y)/y - (функции отсчета) и коэффициента b(k ), определяющего значение функции b(t) в моменты отсчета.
Функция отсчетов представлена графически на рис. 2, где введено обозначение τ = t-k ,ωс = 2πfв. Эта функция в момент времени
t = k достигает максимального значения и равна единице. В момент времени t=(k+1) , где i = 1, 2, 3,.., , функция отсчетов обращается в ноль.
Слайд 6Вопрос1 Дискретизация непрерывных сигналов
Слайд 6
Рис. 2 Рис. 3
Вопрос1 Дискретизация непрерывных сигналов
Слайд 6
Рис. 2 Рис. 3
Слайд 7
Вопрос1 Дискретизация непрерывных сигналов
Слайд 7
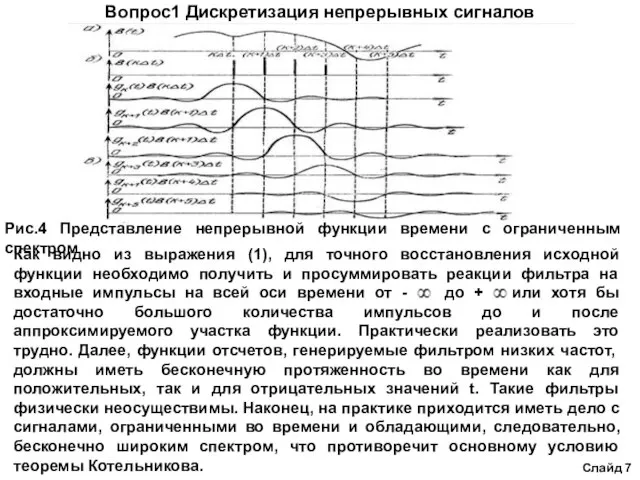
Рис.4 Представление непрерывной функции времени с ограниченным спектром
Как
Вопрос1 Дискретизация непрерывных сигналов
Слайд 7
Рис.4 Представление непрерывной функции времени с ограниченным спектром
Как
Слайд 8Вопрос1 Дискретизация непрерывных сигналов
Вопрос1 Дискретизация непрерывных сигналов

Слайд 9
Вопрос1 Дискретизация непрерывных сигналов
Слайд 9
Вопрос1 Дискретизация непрерывных сигналов
Слайд 9
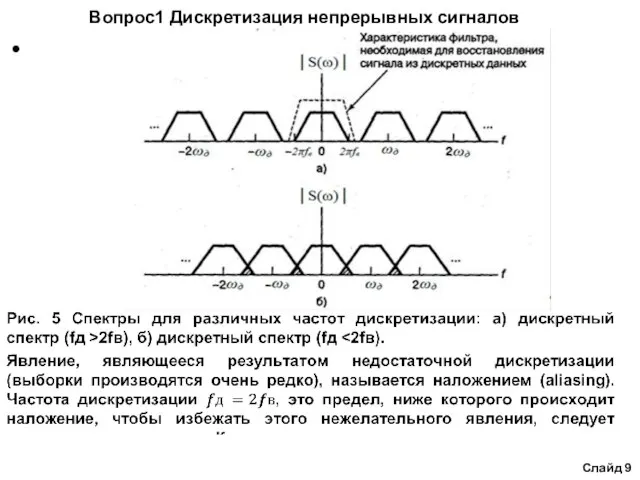
Слайд 10Вопрос1 Дискретизация непрерывных сигналов
Слайд 10
Вопрос1 Дискретизация непрерывных сигналов
Слайд 10

Слайд 11ВОПРОС 2 Квантование по уровню
Слайд 11
Рассмотрим четыре способа описания аналоговой исходной информации.
ВОПРОС 2 Квантование по уровню
Слайд 11
Рассмотрим четыре способа описания аналоговой исходной информации.
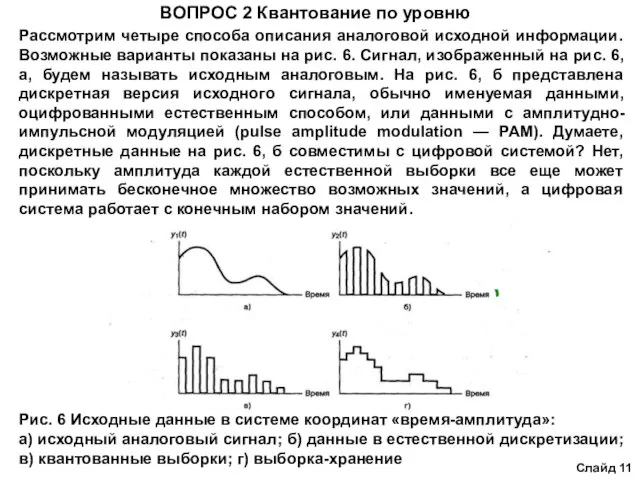
Рис. 6 Исходные данные в системе координат «время-амплитуда»:
а) исходный аналоговый сигнал; б) данные в естественной дискретизации; в) квантованные выборки; г) выборка-хранение
Слайд 12ВОПРОС 2 Квантование по уровню
Даже если дискретные сигналы имеют плоские вершины, возможные
ВОПРОС 2 Квантование по уровню
Даже если дискретные сигналы имеют плоские вершины, возможные

Слайд 12
Слайд 13
ВОПРОС 2 Квантование по уровню
Это искажение, вызванное необходимостью аппроксимации аналогового сигнала квантованными
ВОПРОС 2 Квантование по уровню
Это искажение, вызванное необходимостью аппроксимации аналогового сигнала квантованными
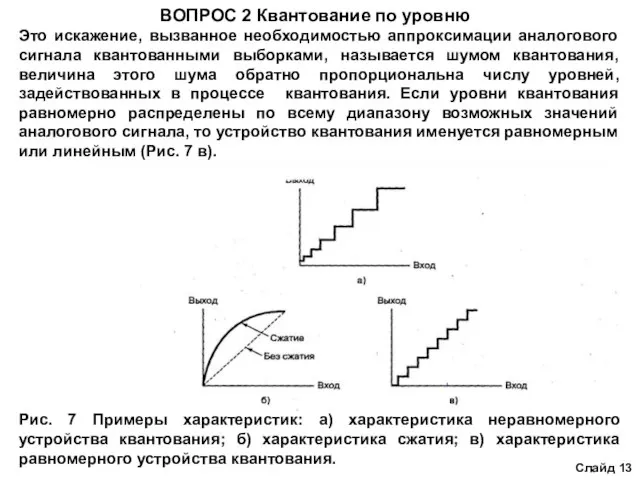
Рис. 7 Примеры характеристик: а) характеристика неравномерного устройства квантования; б) характеристика сжатия; в) характеристика равномерного устройства квантования.
Слайд 13
Слайд 14ВОПРОС 2 Квантование по уровню
Слайд 14
Шаг между уровнями квантования называется интервалом квантования
ВОПРОС 2 Квантование по уровню
Слайд 14
Шаг между уровнями квантования называется интервалом квантования

Недостатком равномерного квантования является меньшая защищенность от шумов квантования малых уровней сигнала. Большое число разрядов в коде (n = 12) при равномерном квантовании приводит к усложнению аппаратуры и неоправданному увеличению тактовой частоты. Устранить указанный существенный недостаток можно, осуществляя неравномерное квантование, которое используется в современных цифровых системах передачи (ЦСП). Сущность неравномерного квантования заключается в следующем. Для малых значений сигналов шаг квантования выбирают минимальным и постепенно увеличивают до максимального для больших значений сигналов. Амплитудная характеристика неравномерного квантователя показана на рис.7 а.
Слайд 15ВОПРОС 2 Квантование по уровню
Слайд 15
При этом для слабых сигналов Рш.кв уменьшается,
ВОПРОС 2 Квантование по уровню
Слайд 15
При этом для слабых сигналов Рш.кв уменьшается,

 Котел Минск 1
Котел Минск 1 Понятие и общая характеристика права собственности на землю
Понятие и общая характеристика права собственности на землю Выцинанка - Храм. Объединение Природа и фантазия
Выцинанка - Храм. Объединение Природа и фантазия Проект. Продвижение кафе
Проект. Продвижение кафе Налог на доходы физических лиц
Налог на доходы физических лиц Архитектура Древнего Рима
Архитектура Древнего Рима Презентация на тему Океаны
Презентация на тему Океаны  Приёмы здоровьесберегающих технологий в начальной школе
Приёмы здоровьесберегающих технологий в начальной школе Методы принятия управленческих решений. Лекция 1
Методы принятия управленческих решений. Лекция 1 Детерминанты коррупции. Социальные последствия коррупции. Тема 2
Детерминанты коррупции. Социальные последствия коррупции. Тема 2 Конституция РФ
Конституция РФ Реинжениринг данных общего архива наблюдений САО РАН
Реинжениринг данных общего архива наблюдений САО РАН Налог на профессиональный доход
Налог на профессиональный доход Развитие универсальных учебных действий при обучении написанию изложения
Развитие универсальных учебных действий при обучении написанию изложения Word-formation in Modern
Word-formation in Modern Тема урока « Наука и семья»8 КЛАСС( химия и литература)
Тема урока « Наука и семья»8 КЛАСС( химия и литература) Процесс многократного рассеяния
Процесс многократного рассеяния Арисова
Арисова Организация деятельности учреждений дополнительного образования с использованием договоров сетевого взаимодействия
Организация деятельности учреждений дополнительного образования с использованием договоров сетевого взаимодействия Экономика Москвы
Экономика Москвы  Гарибян Ирина Ивановна доцент, победитель Фонда «Форум культуры и искусства Узбекистана»
Гарибян Ирина Ивановна доцент, победитель Фонда «Форум культуры и искусства Узбекистана» Формы работы на приходе с молодежью: организация направлений деятельности и приходских кружков
Формы работы на приходе с молодежью: организация направлений деятельности и приходских кружков Презентация1
Презентация1 Борис Иванович Кудрин
Борис Иванович Кудрин Подготовка муниципальных образовательных учреждений к 2011-2012 учебному году
Подготовка муниципальных образовательных учреждений к 2011-2012 учебному году GENTLE DAY
GENTLE DAY Презентация на тему Г. Остер. "Задачник"
Презентация на тему Г. Остер. "Задачник"  Физиологические и мотивационные аспекты волевых действий
Физиологические и мотивационные аспекты волевых действий