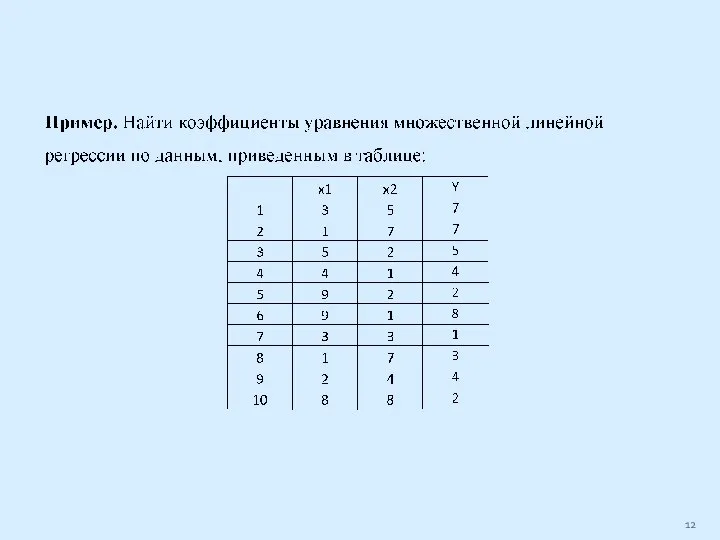
Слайд 10Нахождение коэффициентов уравнения множественной линейной регрессии

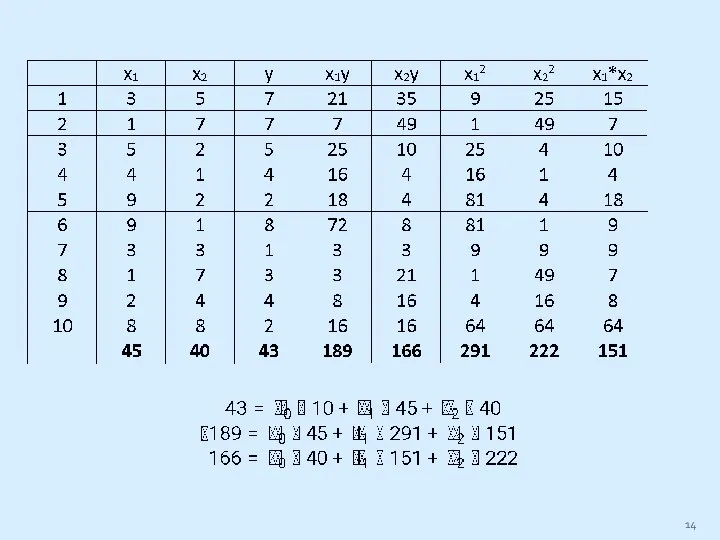
Слайд 11Решение системы нормальных уравнений возможно разными способами. Рассмотрим метод Крамера и матричный

метод.
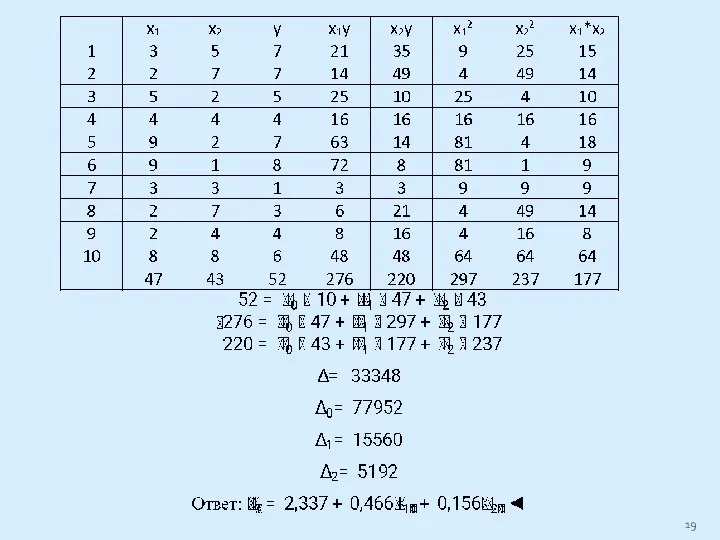
Слайд 17Самостоятельно, используя систему нормальных уравнений (метод Крамера)!
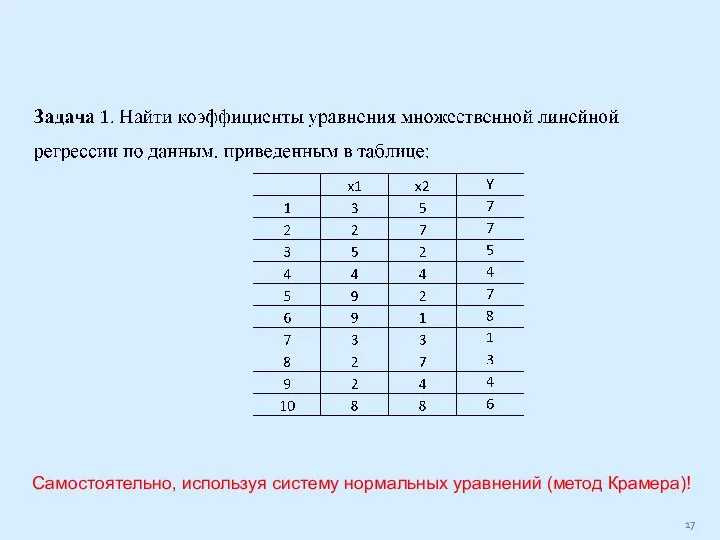
Слайд 20Самостоятельно, используя метод определителей.
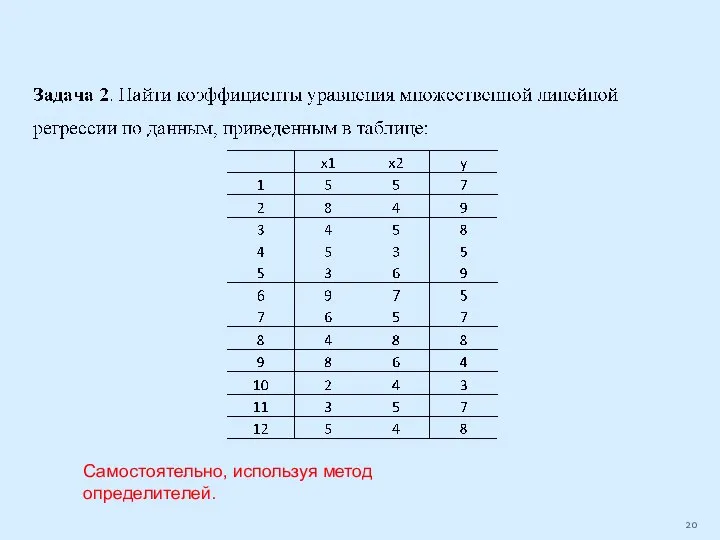
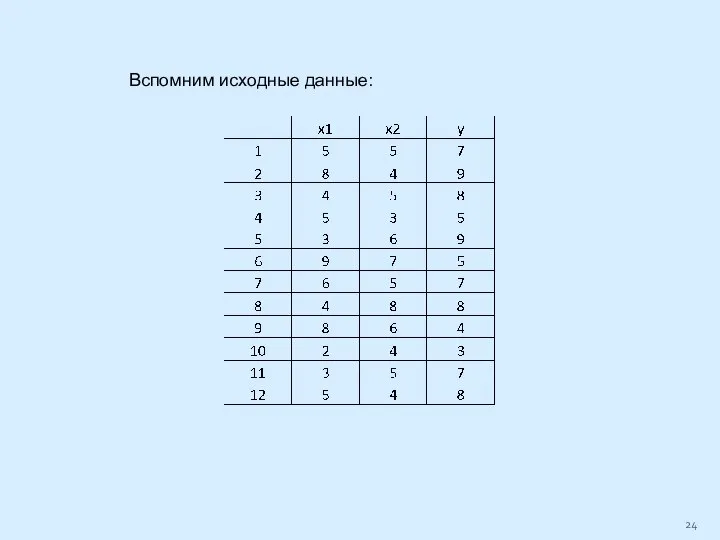
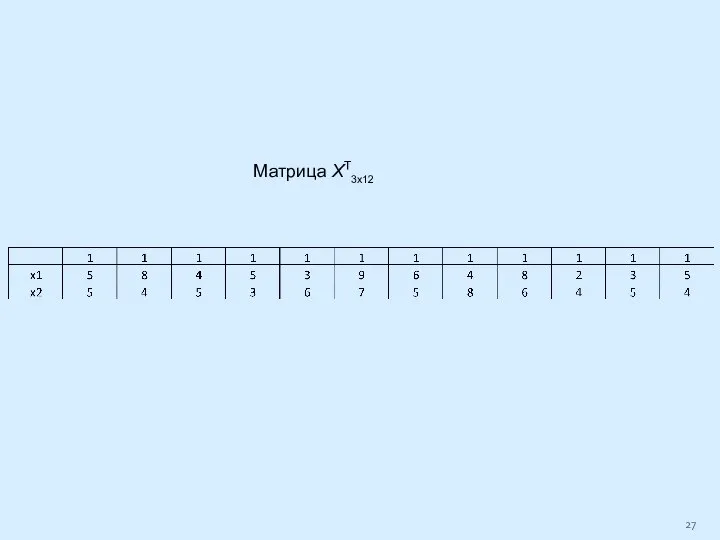
Слайд 25Матрица Х12х3 (1 – единица в первом столбце соответствует переменной
при коэффициенте b0)

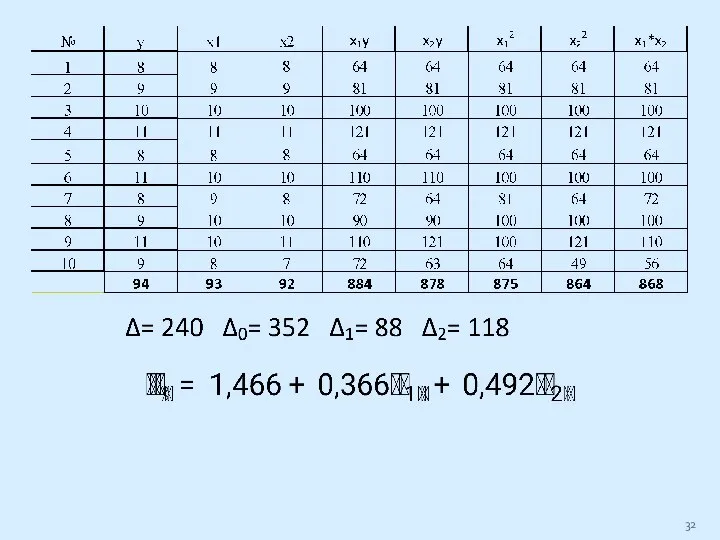
Слайд 31Самостоятельно, используя метод Крамера и матричный метод!
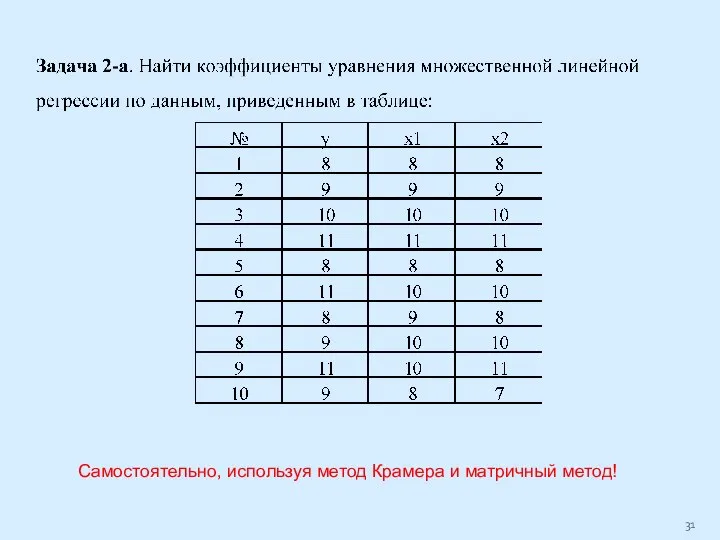
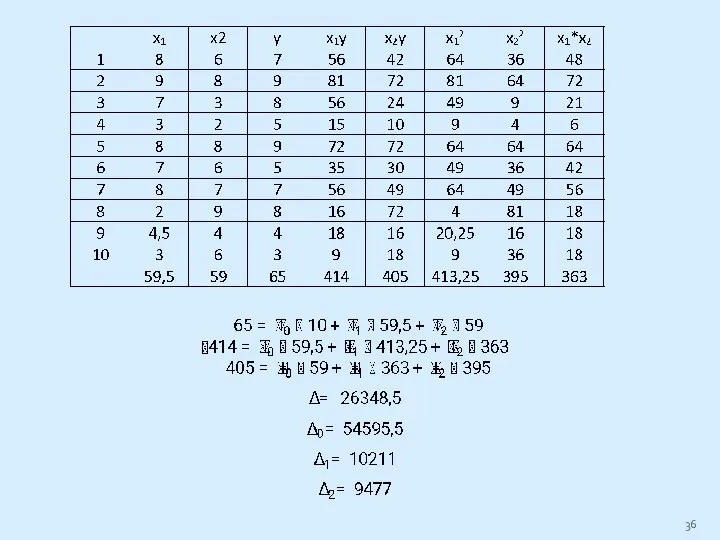
Слайд 34Самостоятельно, используя метод Крамера и матричный метод!
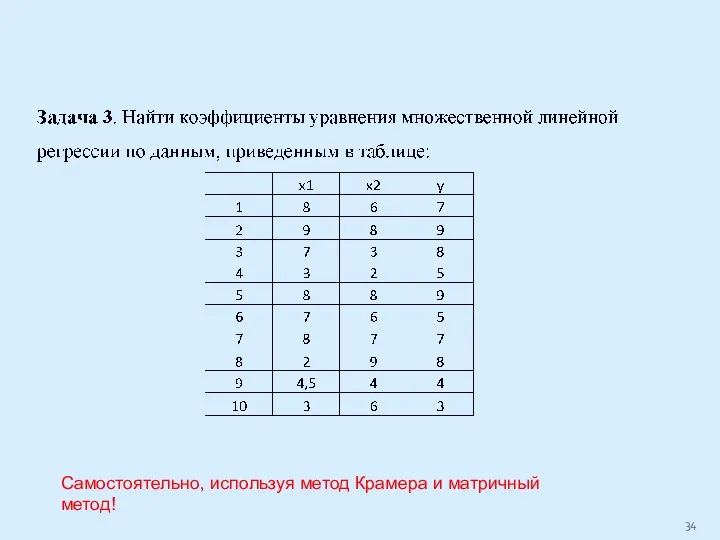
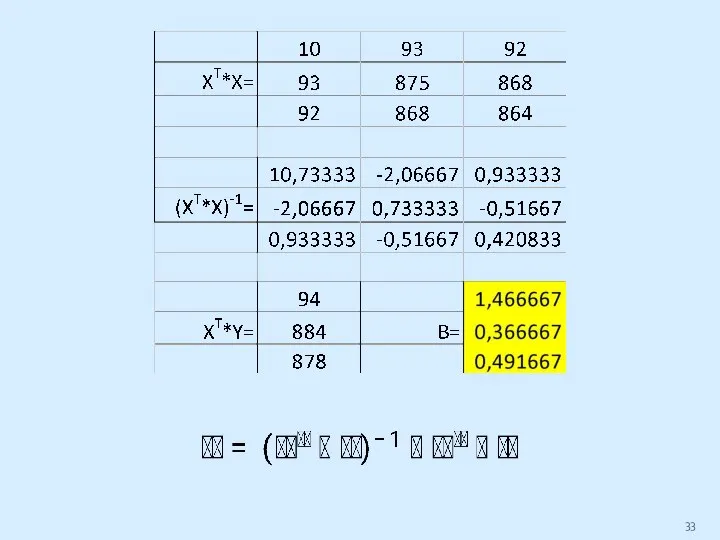
Слайд 37Эта же задача, решенная матричным способом:
◄

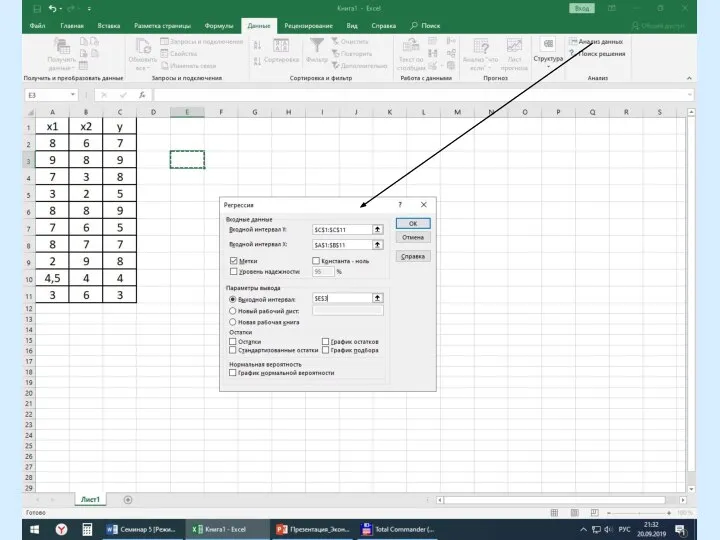
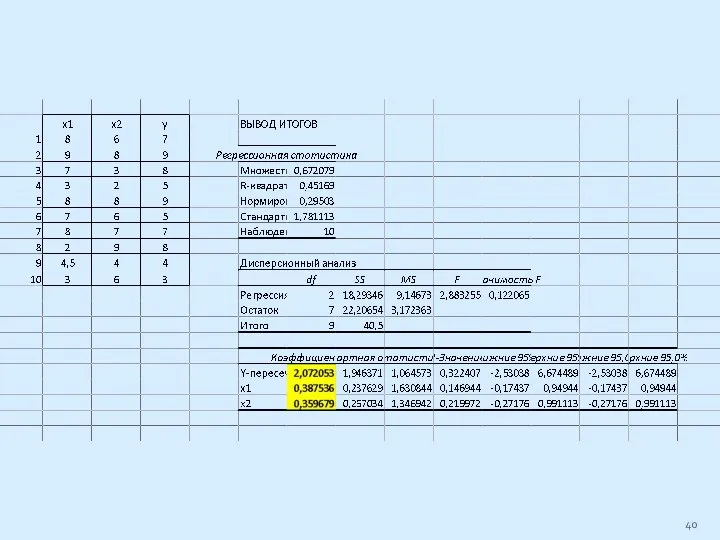
Слайд 38То же, используя программу Регрессия Excel:






























 Web программирование
Web программирование  Почетный гражданин Нижнего Новгорода
Почетный гражданин Нижнего Новгорода Захоронение Сандармох
Захоронение Сандармох Електричне поле. Закон Кулона
Електричне поле. Закон Кулона Архитектура аппаратных средств. Практическое задание № 2. Анализ конфигурации ПК
Архитектура аппаратных средств. Практическое задание № 2. Анализ конфигурации ПК Составление карты узких мест производства вареных колбас
Составление карты узких мест производства вареных колбас Специальные упражнения на развитие общей,мелкой, артикуляционной моторики. Дыхательная гимнастика
Специальные упражнения на развитие общей,мелкой, артикуляционной моторики. Дыхательная гимнастика Kiberry
Kiberry БЫТ ХИМ презентация
БЫТ ХИМ презентация Вокруг нас гаджеты
Вокруг нас гаджеты История елочных украшений
История елочных украшений Использование метода регрессионного анализа для создания тестовых батарей Теплова Ольга
Использование метода регрессионного анализа для создания тестовых батарей Теплова Ольга  NewAvails
NewAvails Презентация_СВ Бакланов_АЛ Шестко
Презентация_СВ Бакланов_АЛ Шестко Общественное объединение «СУТЯЖНИК»1994-2005
Общественное объединение «СУТЯЖНИК»1994-2005 1
1 Презентация на тему Я - ученик 21 века
Презентация на тему Я - ученик 21 века Elizabeth Walsh
Elizabeth Walsh  Добро пожаловать в Хогвартс!
Добро пожаловать в Хогвартс! Переходим на Microsoft Office 2007
Переходим на Microsoft Office 2007 Мой дом - моя семья
Мой дом - моя семья Srednevekovye
Srednevekovye Глаголы. Итальянский язык
Глаголы. Итальянский язык Дворы ОБС Благоустройство 2023 год - МАФ только Счастливый ребенок
Дворы ОБС Благоустройство 2023 год - МАФ только Счастливый ребенок Детская организация Тенгрин герл
Детская организация Тенгрин герл Весельная лодка
Весельная лодка ПАО Челябэнергосбыт
ПАО Челябэнергосбыт Концепции фило и онтогенеза психики в психологии
Концепции фило и онтогенеза психики в психологии