Приемы устного счета. Умножение

Русский способ умножения, или способ изменения сомножителей
Если один сомножитель увеличить в несколько раз, а другой уменьшить во столько же раз, то произведение не измениться.
Примеры:
43 ∙ 16 = 86∙ 8 = 172∙ 4 = 344∙ 2 = 688 ∙ 1 = 688
23 ∙ 27 = 69 ∙ 9 = 207 ∙ 3 = 621 ∙ 1 = 621
125 ∙ 24 = 500 ∙ 6 = 1500 ∙ 2 = 3000 ∙ 1 = 3000

Решите примеры по способу изменения сомножителей
37 ∙ 8 =
53 ∙ 16 =
∙ 18 =
∙ 24 =
∙ 32 =
74 ∙ 4 = 148 ∙ 2 = 296 ∙ 1 = 296
106 ∙ 8 = 212 ∙4 =424∙2 =848∙1= 848
68 ∙ 9 = 204 ∙ 3 = 612 ∙ 1 = 612
90∙12 = 270∙4 =540∙2=1080∙1= 1080
74∙16 = 148∙ 8 = 296∙4 = 592 ∙2 = 1184 ∙ 1 = 1184

Умножение по способу Гаусса
Известный математик Гаусс заметил, что всякое умножение двух целых чисел можно привести к умножению одного из них на 5, 2 и 1 или на круглые числа, записанные только этими цифрами ( и нулем ), путем замены другого сомножителя суммой или разностью соответствующим образом подобранных чисел

Пример 1. 89 ∙ 27.
Представим число 27 в виде суммы трех чисел (20 + 5 + 2) получим
89∙ 27 =89 ∙ (20 + 5 + 2)= 1780 + 445 + 178 =2403
Пример 2. 53∙ 89 = 53∙ (100 – 10 - 1) = 5300 –
-530 – 53 = 4770 – 53 = 4717
Пример 3. 47 ∙ 91 = 47 ∙ ( 100 – 10 + 1)= 4700-
- 470 + 47 = 4230 + 47 = 4277

Решите примеры по способу Гаусса
45 ∙ 31 =
64 ∙ 88 =
57 ∙ 92 =
45 ∙ (30 + 1) = 45 ∙ 30 + 45 ∙ 1=
= 1350 + 45 = 1395
64 ∙ (90-2) = 64 ∙ 90 - 64∙ 2=
=5760 – 128 = 5632
57 ∙ (90 + 2 ) = 57 ∙ 90 + 57 ∙ 2 =
= 5130 + 114 = 5244

Умножение на 5 ; 50 ; 0,5 , 25

Вычисли
138 ∙ 5 =
117 ∙ 50 = 468 ∙ 0,5 =
284 ∙ 25 =

Умножение на 15 ; 101 ; 11

Чтобы умножить двузначное число на 101 , надо мысленно приписать к данному числу ( справа или слева) еще раз само это число.
Пример.
58 ∙ 101 = 5858 , так как 58 ∙ 101 = 58 ∙ 100 +
+ 58 ∙ 1 = 5800 + 58 = 5858

Умножение на 11 , когда сумма двух радом стоящих цифр множимого меньше десятки
Пример 1. 25 ∙ 11
При умножении первая цифра множимого будет первой цифрой произведения (2); вторая цифра множимого будет последней цифрой произведения (5); средняя цифра произведения равна сумме цифр множимого (2 + 5 = 7).
25 ∙ 11 = 275

Пример 2. 354 ∙ 11
Крайние цифры множимого будут крайними цифрами произведения. Первая средняя цифра произведения равняется сумме первой и второй цифр множимого (3 + 5 = 8); вторая средняя цифра произведения равна сумме второй и третьей цифр множимого
(5 + 4 = 9)
354 ∙ 11 = 3894

Пример 3. 4327 ∙ 11
4 - первая цифра произведения.
4 + 3 = 7 -вторая цифра произведения.
3 + 2 = 5 – третья цифра произведения.
2 + 7 = 9 - четвертая цифра произведения.
7 - последняя цифра произведения.
Следовательно,
4327 ∙ 11 = 47597

Умножение на 11 , когда сумма двух радом стоящих цифр множимого равна 10 или больше.
Когда при умножении любого числа на 11 сумма двух рядом стоящих цифр множимого равна десяти или больше десяти, то первую цифру полученной суммы прибавляем к следующей, старшей цифре множимого; причем сложение цифр надо производить только с конца.

Пример 1. 68 ∙ 11
8 - последняя цифра произведения.
8 + 6 = 14 - 4 –вторая цифра
произведения 1 в уме;
6 да 1 в уме , будет 7 - первая цифра
произведения.
68 ∙ 11 = 748

Пример 2. 587 ∙ 11
7 – последняя цифра произведения
7 + 8 = 15 – 5 вторая цифра, считая с конца ;
один в уме.
8 + 5 да один в уме, будет 14 (4 третья
цифра с конца ; 1 в уме)
5 да 1 в уме, будет 6 –первая цифра
произведения.
587 ∙ 11 = 6457

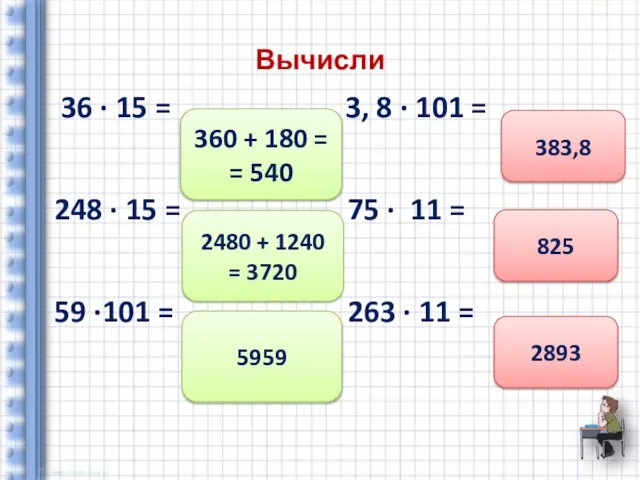
Вычисли
36 ∙ 15 = 3, 8 ∙ 101 =
248 ∙ 15 = 75 ∙ 11 =
59 ∙101 = 263 ∙ 11 =
360 + 180 = = 540
2480 + 1240 = 3720
5959
383,8
825
2893