Приложение к лекции 2

1а Степенная функция
1) D ( f ) = ( – ∞, 0) ∪ ( 0, + ∞)
2) E ( f ) = {1}
3) четная: (- x) 0 = x 0
4) постоянная
5) ограниченная
6) непериодическая

1б Степенная функция
1) D ( f ) = ( – ∞, + ∞)
2) E ( f ) = ( – ∞, + ∞)
3) нечетная: (- x)1 = - x1
4) возрастает на ( – ∞, + ∞)
5) неограниченная
6) непериодическая

1в Степенная функция
n нечетное натуральное число > 2
1) D ( f ) = ( – ∞, + ∞)
2) E ( f ) = ( – ∞, + ∞)
3) нечетная: (- x)n = - xn
4) возрастает на ( – ∞, + ∞)
5) неограниченная
6) непериодическая

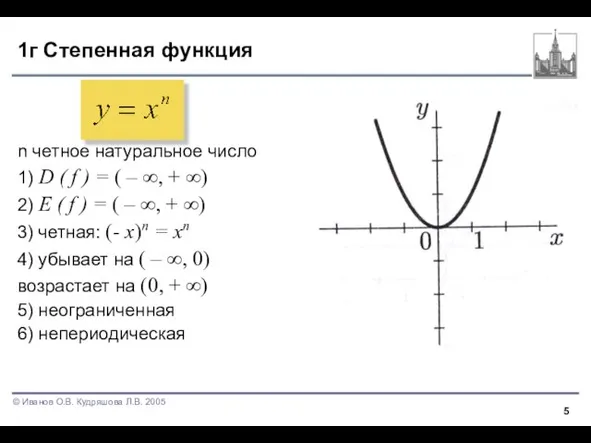
1г Степенная функция
n четное натуральное число
1) D ( f ) = ( – ∞, + ∞)
2) E ( f ) = ( – ∞, + ∞)
3) четная: (- x)n = xn
4) убывает на ( – ∞, 0)
возрастает на (0, + ∞)
5) неограниченная
6) непериодическая

1д Степенная функция
n нечетное натуральное число
1) D ( f ) = ( – ∞, 0 ) ∪ ( 0, + ∞)
2) E ( f ) = ( – ∞, 0 ) ∪ ( 0, + ∞)
3) нечетная: (- x) -n = - x -n
4) убывает на ( – ∞, 0) ∪ ( 0, + ∞)
5) неограниченная
6) непериодическая

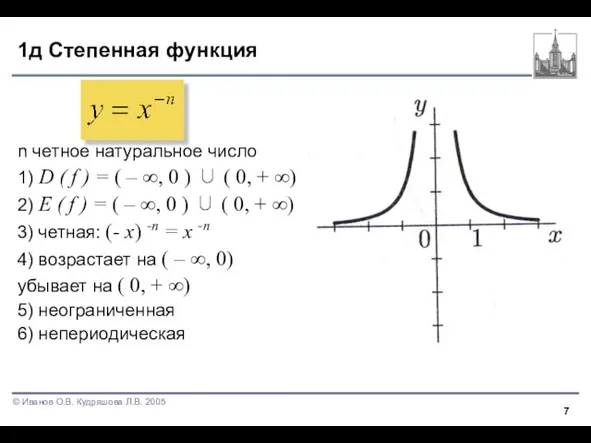
1д Степенная функция
n четное натуральное число
1) D ( f ) = ( – ∞, 0 ) ∪ ( 0, + ∞)
2) E ( f ) = ( – ∞, 0 ) ∪ ( 0, + ∞)
3) четная: (- x) -n = x -n
4) возрастает на ( – ∞, 0)
убывает на ( 0, + ∞)
5) неограниченная
6) непериодическая

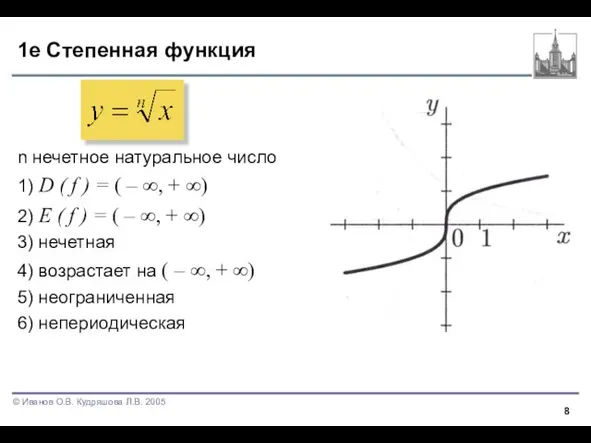
1е Степенная функция
n нечетное натуральное число
1) D ( f ) = ( – ∞, + ∞)
2) E ( f ) = ( – ∞, + ∞)
3) нечетная
4) возрастает на ( – ∞, + ∞)
5) неограниченная
6) непериодическая

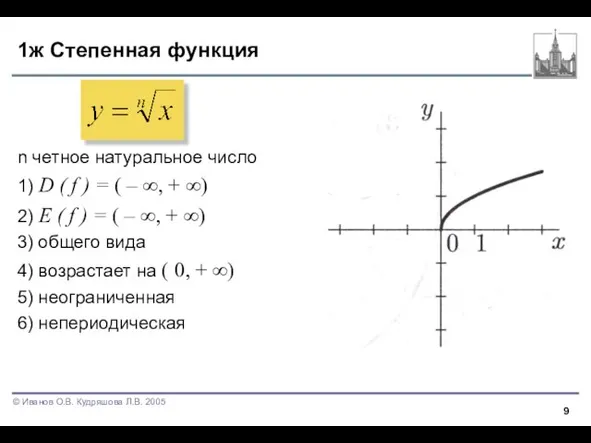
1ж Степенная функция
n четное натуральное число
1) D ( f ) = ( – ∞, + ∞)
2) E ( f ) = ( – ∞, + ∞)
3) общего вида
4) возрастает на ( 0, + ∞)
5) неограниченная
6) непериодическая

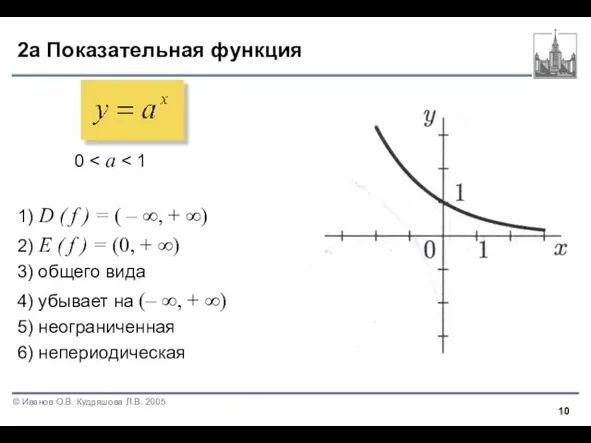
2а Показательная функция
0 < a < 1
1) D ( f ) = ( – ∞, + ∞)
2) E ( f ) = (0, + ∞)
3) общего вида
4) убывает на (– ∞, + ∞)
5) неограниченная
6) непериодическая

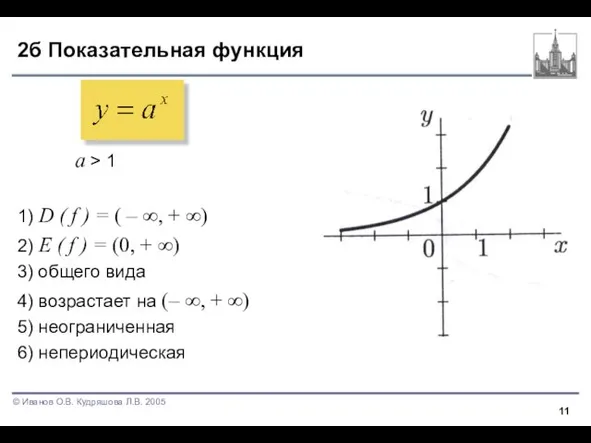
2б Показательная функция
a > 1
1) D ( f ) = ( – ∞, + ∞)
2) E ( f ) = (0, + ∞)
3) общего вида
4) возрастает на (– ∞, + ∞)
5) неограниченная
6) непериодическая

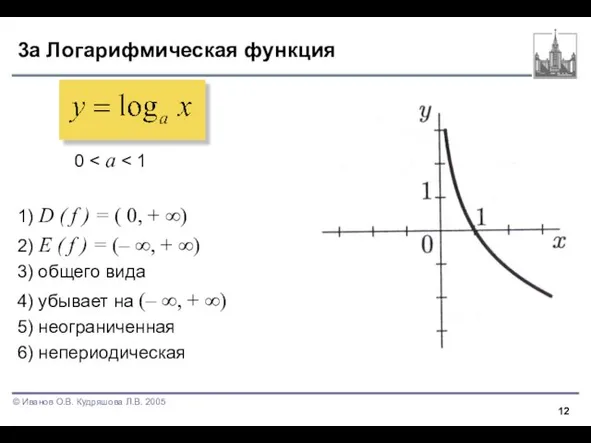
3a Логарифмическая функция
0 < a < 1
1) D ( f ) = ( 0, + ∞)
2) E ( f ) = (– ∞, + ∞)
3) общего вида
4) убывает на (– ∞, + ∞)
5) неограниченная
6) непериодическая

3б Логарифмическая функция
a > 1
1) D ( f ) = ( 0, + ∞)
2) E ( f ) = (– ∞, + ∞)
3) общего вида
4) возрастает на (– ∞, + ∞)
5) неограниченная
6) непериодическая

4 Тригонометрические функции
4а синус
4б косинус
4в тангенс
4г котангенс

5 Обратные тригонометрические функции
5а арксинус
5б арккосинус
5в арктангенс
5г арккотангенс

Преобразование: параллельный перенос
График функции
y = f (x) + b
получается из графика
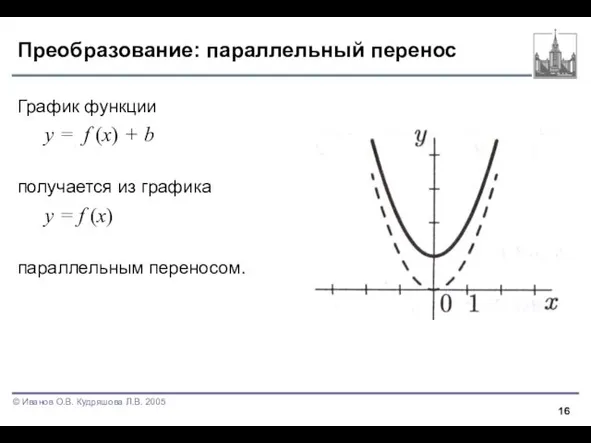
y = f (x)
параллельным переносом.

Преобразование: параллельный перенос (2)
График функции
y = f (x + a)
получается из графика
y = f (x)
параллельным переносом.

Преобразование: растяжение (сжатие)
График функции
y = A f (x), A > 0
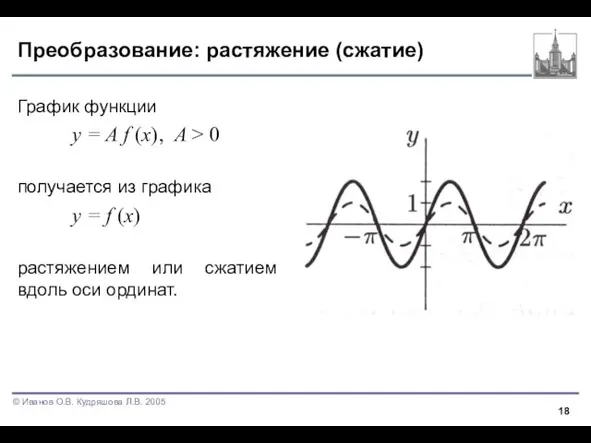
получается из графика
y = f (x)
растяжением или сжатием вдоль оси ординат.

Преобразование: растяжение (сжатие)
График функции
y = f (ax), a > 0
получается из графика
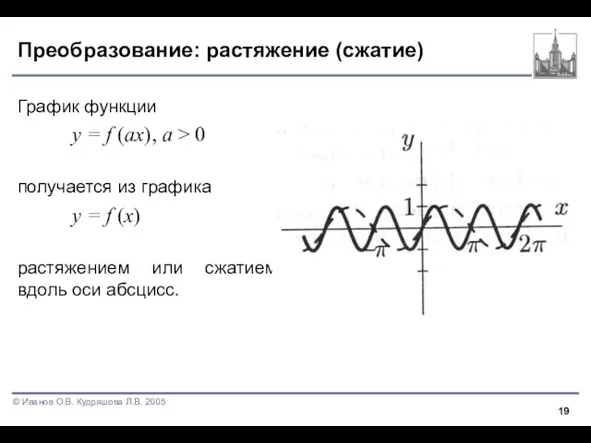
y = f (x)
растяжением или сжатием вдоль оси абсцисс.

Преобразование: зеркальное отражение
График функции
y = – f (x)
получается из графика
y = f (x)
зеркальным отражением относительно оси абсцисс.