Применение формул сокращённого умножения

Примеры основных формул сокращённого умножения:
(a + b)² = a² + 2ab + b²
(a – b)² = a² – 2ab + b²
a² – b² = (a – b)(a + b)
a³ + b³ = (a + b)(a² – ab + b²)
a³ – b³ = (a – b)(a² + ab + b²)
(a + b)³ = a³ + 3a²b + 3ab² + b³
(a – b)³ = a³ – 3a²b + 3ab² – b³
А также:

Исторические сведения
Формулы сокращённого умножения были известны еще 4000 лет назад. Ученые Древней Греции представляли величины не числами или буквами, а отрезками прямых. Вместо «произведение a и b» говорилось «прямоугольник, содержащийся между а и в», вместо а² - «квадрат на отрезке а».

Евклид «Начала»

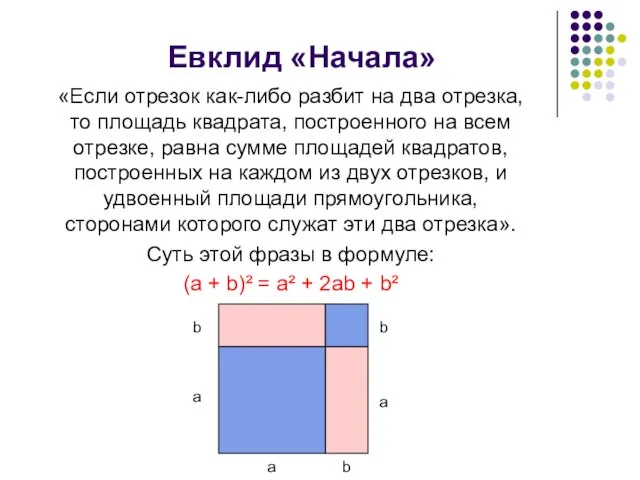
Евклид «Начала»
«Если отрезок как-либо разбит на два отрезка, то площадь квадрата, построенного на всем отрезке, равна сумме площадей квадратов, построенных на каждом из двух отрезков, и удвоенный площади прямоугольника, сторонами которого служат эти два отрезка».
Суть этой фразы в формуле:
(a + b)² = a² + 2ab + b²
a
b
a
b
a
b

Применение формул сокращённого умножения:
в алгебре
в геометрии

Разложение многочленов на множители
(a² + 1)² – 4a² = ((a² + 1) – 2a)((a² + 1) + +2a) = (a² + 1 – 2a)(a² + 1 + 2a) = (a² – 2a + +1)(a² + 2a + 1) = (a - 1)²(a + 1)²
a² – b² – a – b = (a – b)(a + b)–(a + b) =(a + + b)(a – b – 1)
В разложении данных многочленов использовались формулы:
разность квадратов
квадрат разности
квадрат суммы

Представление выражения в виде многочлена
.
Ответ:

Решение уравнения
(x – 2)³ + (x + 2)³ = 2(x – 3)(x² + 3x + 9)
x³ – 6x² + 12x – 8 + x³ + 6x² + 12x + 8 = 2(x³ – 27)
2x³ + 24x = 2x³ – 54
24x = - 54
x = - 2,25
1 способ
В решении данного уравнения первым способом использовались формулы:
1) куб разности
2) куб суммы

Решение уравнения
(x – 2)³ + (x + 2)³ = 2(x – 3)(x² + 3x + 9)
(x-2+x+2)((x-2)² - (x-2)(x+2) + (x+2)² = 2(x³-27)
2x(x² – 4x + 4 – x² + 4 + x² + 4x +4) = 2x³ – 54
2x(x² + 12) = 2x³ – 54
2x³ + 24x – 2x³ = - 54
24x = - 54
x = - 2,25
2 способ
В решении данного уравнения вторым способом использовались формулы:
1) сумма кубов; 2) квадрат разности; 3) квадрат суммы;
4) разность квадратов.

Доказательство неравенства
Доказать неравенство:
, что верно.

Делимость
Докажем, что число n³ – n, где n – натуральное число, делится на 6:
n³ – n = n(n² – 1) = n(n – 1)(n + 1)
Заданное число есть произведение трёх последовательных чисел, из которых одно обязательно делится на 3 и хотя бы одно делится на 2. Если произведение делится и на 3, и на 2, то оно делится и на 6.

Тождественные преобразования
Докажем тождество:
.
,
,
.
Итак, с помощью тождественных преобразований с применением формул сокращённого умножения мы левую часть равенства привели к виду правой его части. Тождество доказано.

Задача Пифагора
«Всякое нечётное число, кроме единицы, есть разность двух квадратов».
Решение:
n – натуральное число
(n + 1)² – n² = (n + 1 – n)(n + 1 + n) = 2n + 1
2n + 1 – нечётное число

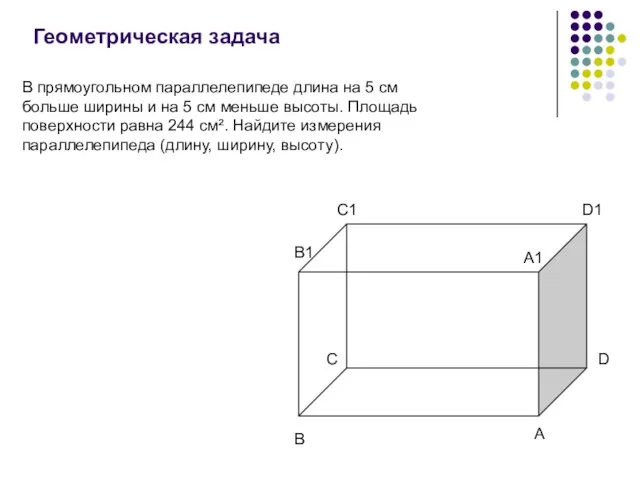
Геометрическая задача
C
A1
В прямоугольном параллелепипеде длина на 5 см больше ширины и на 5 см меньше высоты. Площадь поверхности равна 244 см². Найдите измерения параллелепипеда (длину, ширину, высоту).

Геометрическая задача
Пусть x см – AB(длина), тогда (x+5) cм – AA1(высота), (x-5) см – AD(ширина).
S = 2SABCD + 2SAA1D1D + 2SAA1B1B, а по условию – 244 см²
SABCD = x(x-5); SAA1D1D = (x-5)(x+5);
SAA1B1B = x(x+5)
Составим и решим уравнение:
2x(x-5) + 2(x-5)(x+5) + 2x(x+5) = 244
x(x-5) + (x-5)(x+5) + x(x+5) = 122
x² – 5x + x² – 5² + x² + 5x = 122
3x² = 122+25
3x² = 147
x² = 49, x > 0 (по смыслу задачи)
x = 7
A
B
C
D
B1
A1
C1
D1

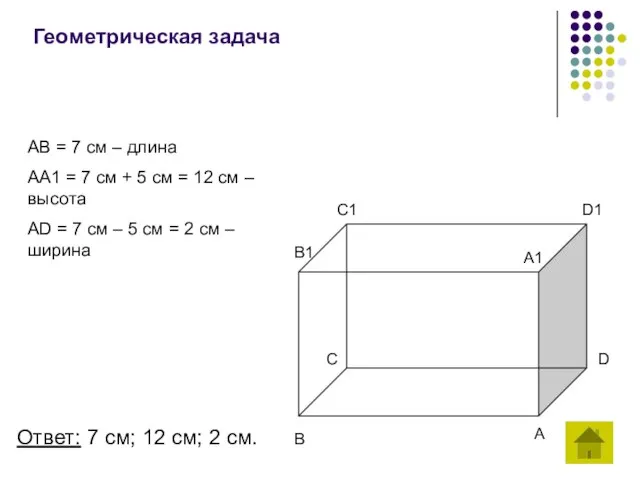
Геометрическая задача
AB = 7 см – длина
AA1 = 7 см + 5 см = 12 см – высота
AD = 7 см – 5 см = 2 см – ширина
A
B
C
D
B1
A1
C1
D1
Ответ: 7 см; 12 см; 2 см.