Содержание
- 2. Плоские и пространственные кривые Плоской является такая кривая линия, которая лежит в плоскости и, следовательно, при
- 3. КРИВЫЕ ЛИНИИ И ПОВЕРХНОСТИ Кривые линии Определение: Кривую линию можно рассматривать как траекторию движущейся точки на
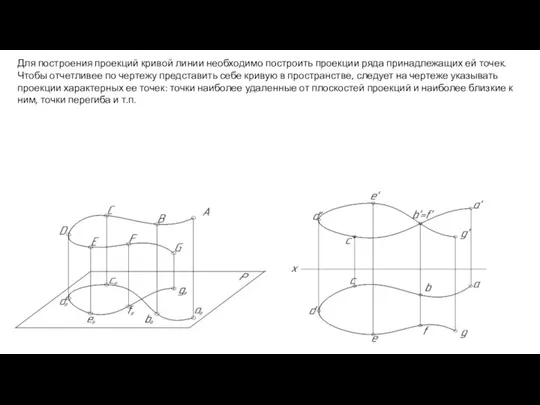
- 4. Для построения проекций кривой линии необходимо построить проекции ряда принадлежащих ей точек. Чтобы отчетливее по чертежу
- 5. Поверхность представляет собой множество последовательных положений линии, перемещающейся в пространстве. Эту линию называют образующей поверхности.
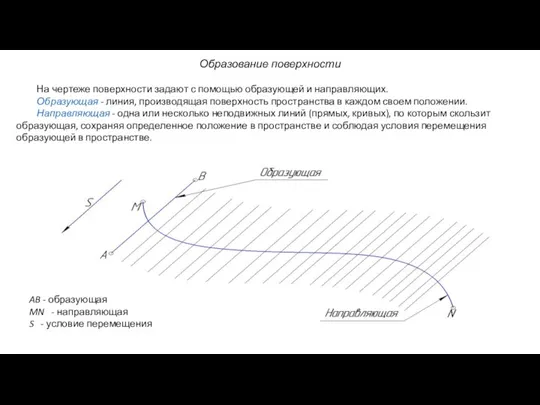
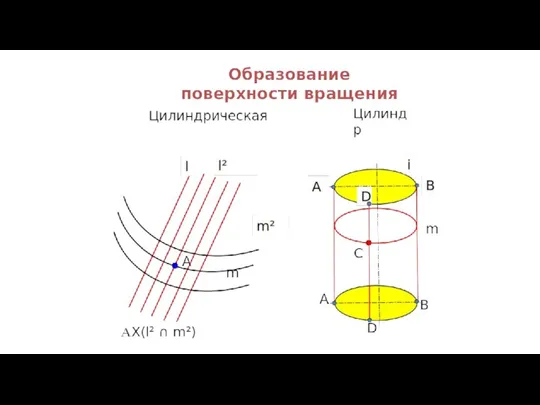
- 6. Образование поверхности На чертеже поверхности задают с помощью образующей и направляющих. Образующая - линия, производящая поверхность
- 7. Образование поверхностей l l' l" ln m m' m" mn A C B l– образующая поверхности;
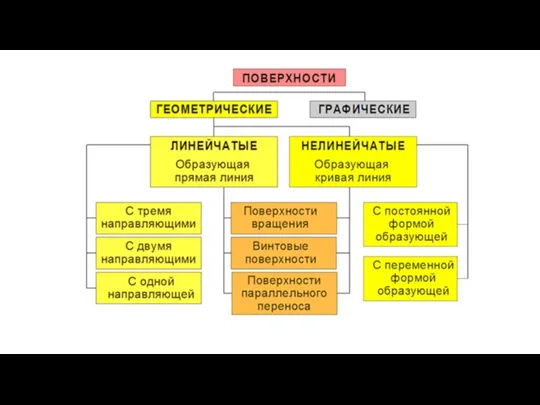
- 8. Существует три способа задания поверхности: 1. Аналитический − поверхность задается уравнением;
- 9. 2. Каркасный − поверхность задается совокупностью точек и линий;
- 10. g – образующая поверхности; d – направляющая поверхности. 3. Кинематический − поверхность рассматривается как совокупность последовательных
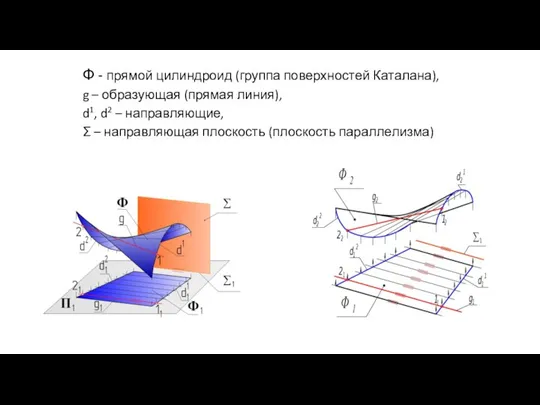
- 11. Ф - прямой цилиндроид (группа поверхностей Каталана), g – образующая (прямая линия), d1, d2 – направляющие,
- 12. Геометрическая поверхность Графическая поверхность
- 13. Определитель поверхности Это совокупность независимых условий, однозначно задающих поверхность. Определитель состоит из двух частей: Геометрическая (Г)
- 14. Одна и та же поверхность может быть образована различными способами, следовательно иметь несколько определителей. а) цилиндр
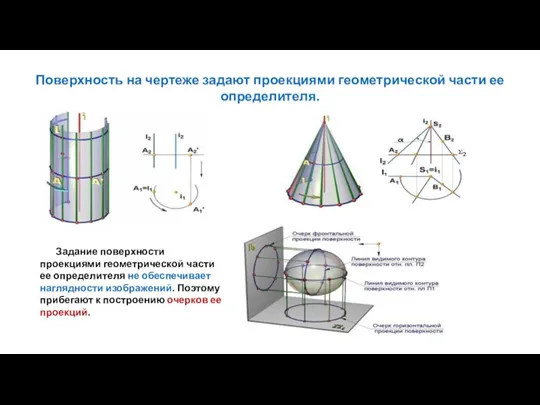
- 15. Поверхность на чертеже задают проекциями геометрической части ее определителя. Задание поверхности проекциями геометрической части ее определителя
- 16. Очерк поверхности Очерк поверхности – это линия пересечения плоскости проекций с проецирующей поверхностью, касательной к заданной
- 17. Чтобы задать поверхность на чертеже необходимо: 1. Построить проекции определителя. 2. Построить проекции очерковых образующих поверхности
- 18. Поверхности Поверхностью называется совокупность всех последовательных положений линий, непрерывно перемещающихся в пространстве. Линия, образующая поверхность, называется
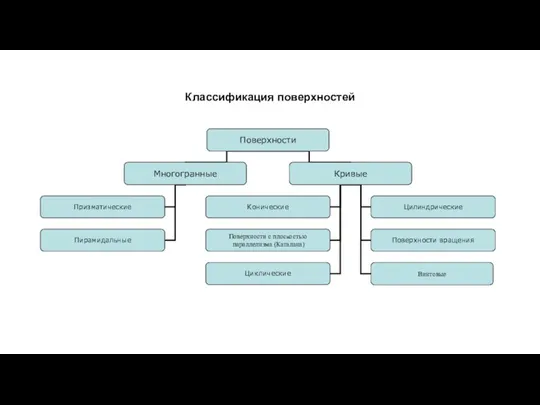
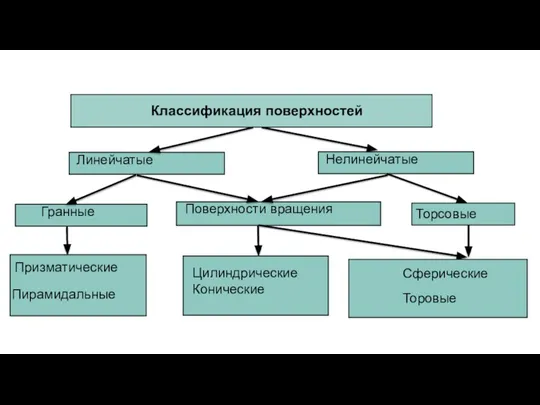
- 19. Классификация поверхностей
- 20. Классификация поверхностей
- 22. Линейчатые поверхности с тремя направляющими Поверхность косого клина Поверхность косого перехода
- 23. Линейчатые поверхности с двумя направляющими и направляющей плоскостью или плоскостью параллелизма (поверхности Каталана)
- 24. Поверхности Каталана (с плоскостью параллелизма) – неразвертывающиеся линейчатые поверхности Цилиндроид – поверхность, у которой обе направляющие
- 25. Коноид – поверхность, у которой одна направляющая прямая, другая – кривая.
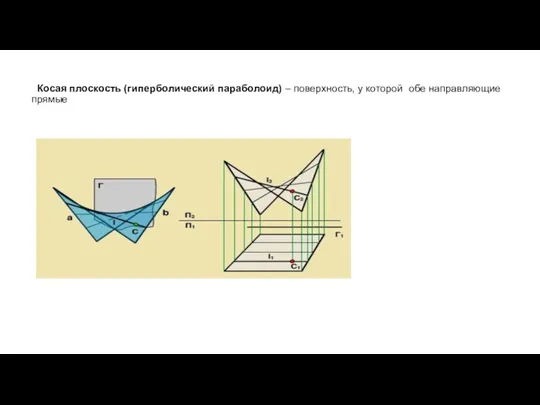
- 26. Косая плоскость (гиперболический параболоид) – поверхность, у которой обе направляющие прямые
- 27. Линейчатые поверхности с одной направляющей Торсы S – реальная точка S∞ - несобственная точка пространства
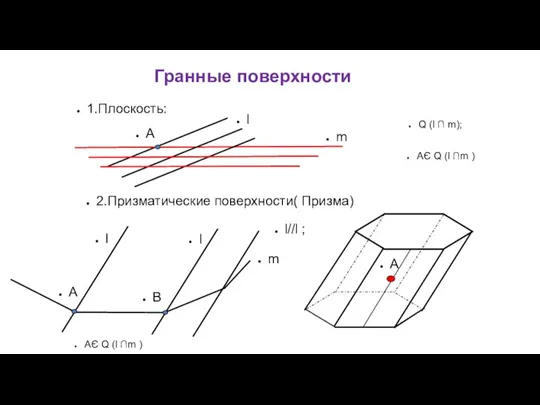
- 28. Гранные поверхности Призматическая Пирамидальная
- 29. Гранные поверхности 2.Призматические поверхности( Призма) 1.Плоскость: l m A AЄ Q (l ∩m ) Q (l
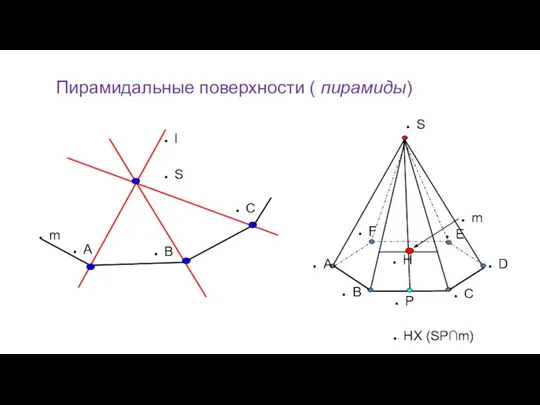
- 30. Пирамидальные поверхности ( пирамиды) S l A B C m S A B C D F
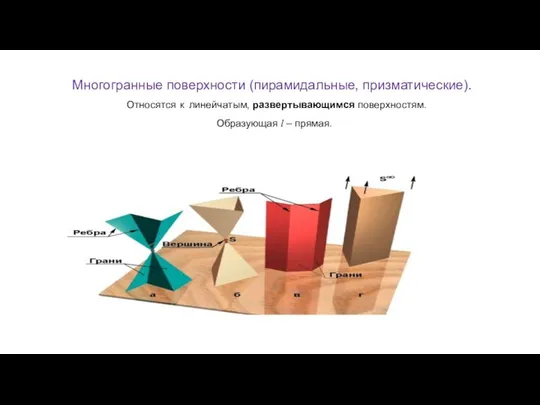
- 31. Многогранные поверхности (пирамидальные, призматические). Относятся к линейчатым, развертывающимся поверхностям. Образующая l – прямая.
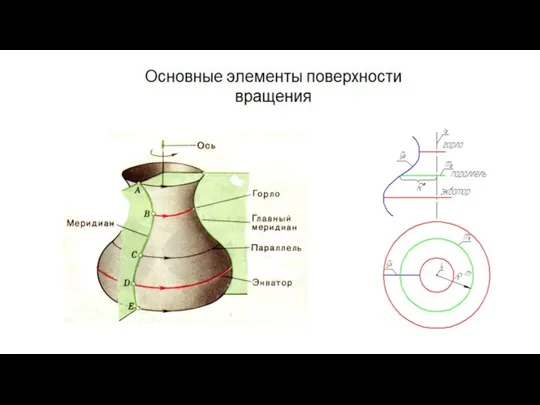
- 32. Поверхности вращения
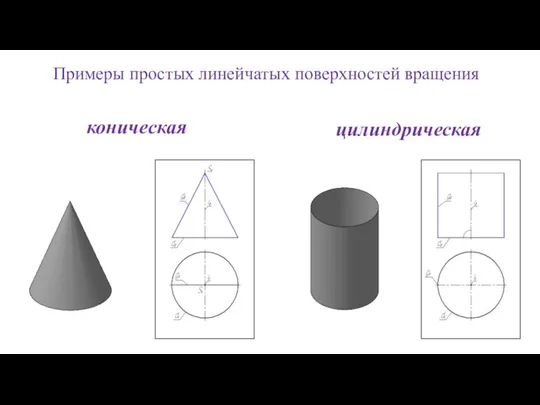
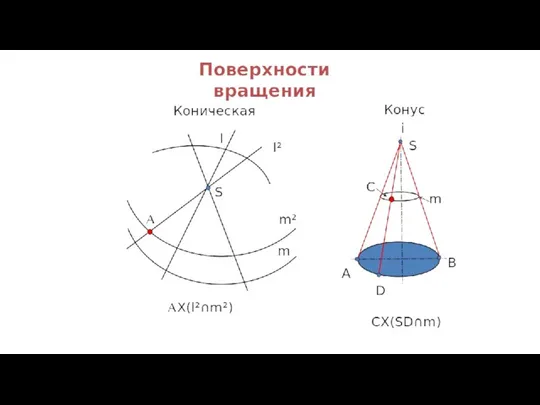
- 33. Примеры простых линейчатых поверхностей вращения коническая цилиндрическая
- 34. Цилиндрические поверхности Цилиндрическая поверхность образуется движением прямой линии, скользящей по некоторой неподвижной замкнутой или незамкнутой
- 36. Конические поверхности Коническая поверхность образуется движением прямой линии, скользящей по некоторой неподвижной замкнутой или незамкнутой
- 37. Поверхности вращения 2-го порядка. Цилиндр вращения –проецирующая поверхность. Комплексный чертеж
- 38. 1). Цилиндр вращения (прямой круговой цилиндр)– линейчатая, развертываемая, алгебраическая поверхность второго порядка, получается при вращении прямой
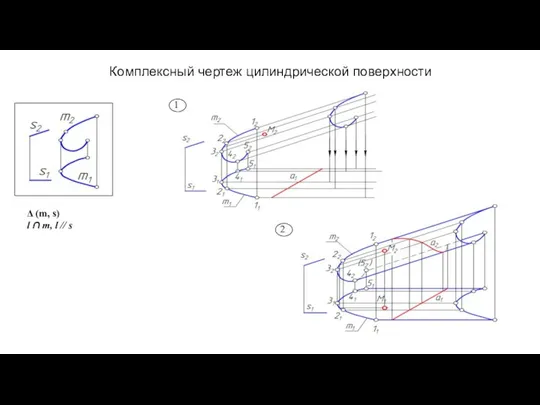
- 39. Комплексный чертеж цилиндрической поверхности 1 2 Δ (m, s) l ∩ m, l // s
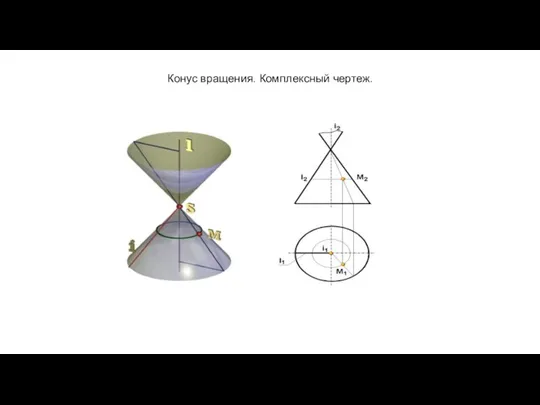
- 41. Конус вращения. Комплексный чертеж.
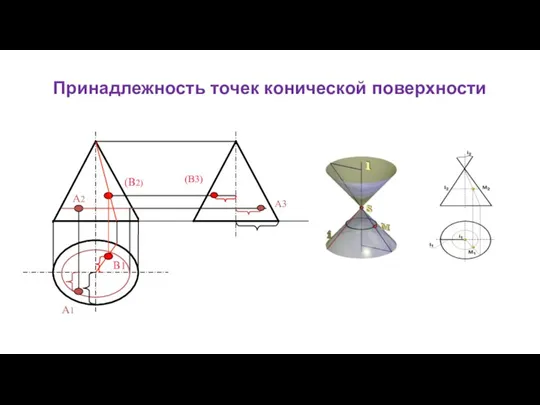
- 42. Коническая поверхность общего вида - образующая SA проходит через некоторую неподвижную точку S (вершину) и последовательно
- 43. SA - образующая MN – направляющая K ∈ Кон ⇒ k' → k - ? Коническая
- 44. Коническая поверхность общего вида - образующая SA проходит через некоторую неподвижную точку S (вершину) и последовательно
- 45. SA - образующая MN – направляющая K ∈ Кон ⇒ k' → k - ? K
- 46. SA - образующая MN – направляющая K ∈ Кон ⇒ k' → k - ? K
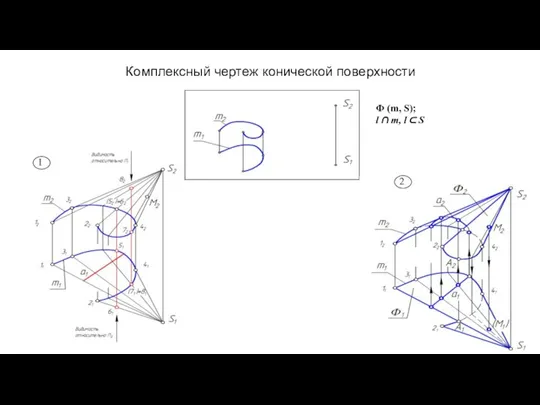
- 47. Комплексный чертеж конической поверхности 2 1 Φ (m, S); l ∩ m, l ⊂ S
- 48. Сфера Сфера образуется вращением окружности вокруг оси (i) Комплексный чертеж сферы
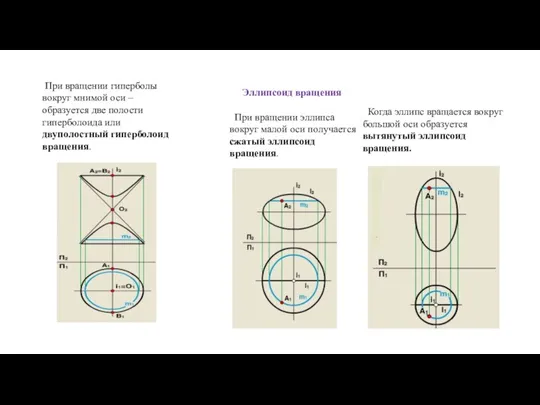
- 49. Однополостный гиперболоид вращения. Комплексный чертеж. Гипербола имеет две оси – действительную и мнимую. При вращении гиперболы
- 50. При вращении гиперболы вокруг мнимой оси – образуется две полости гиперболоида или двуполостный гиперболоид вращения. Эллипсоид
- 51. Параболоид вращения Эта поверхность образуется при вращении параболы вокруг своей оси. При вращении дуги окружности, образуется
- 52. Тор - поверхность вращения 4-го порядка Если R Если R > либо = r, то окружность
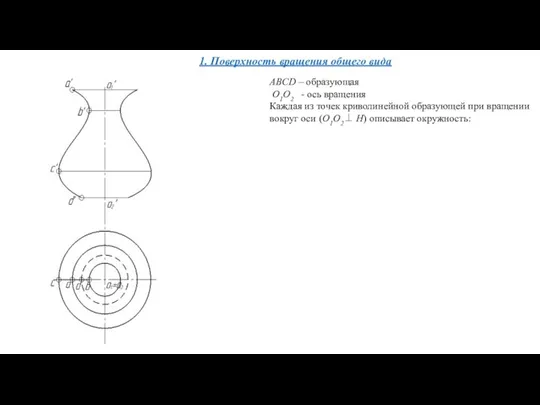
- 53. ПОВЕРХНОСТИ ВРАЩЕНИЯ 1. Поверхность вращения общего вида Поверхностью вращения общего вида называют поверхность, которая образуется произвольной
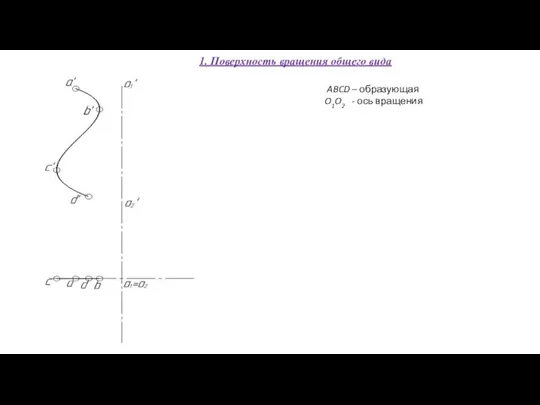
- 55. 1. Поверхность вращения общего вида ABCD – образующая O1O2 - ось вращения
- 56. 1. Поверхность вращения общего вида ABCD – образующая O1O2 - ось вращения Каждая из точек криволинейной
- 57. ABCD – образующая O1O2 - ось вращения Каждая из точек криволинейной образующей при вращении вокруг оси
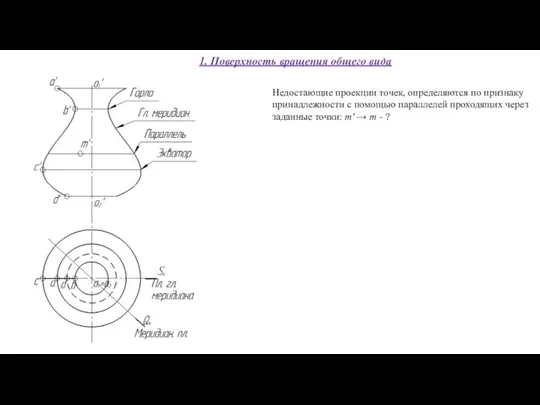
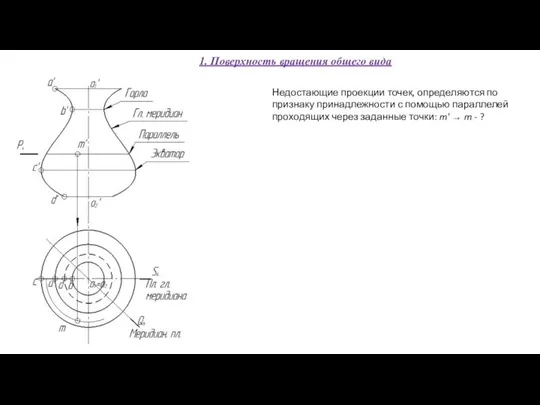
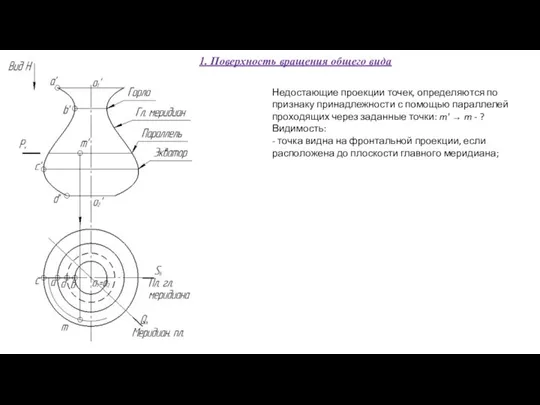
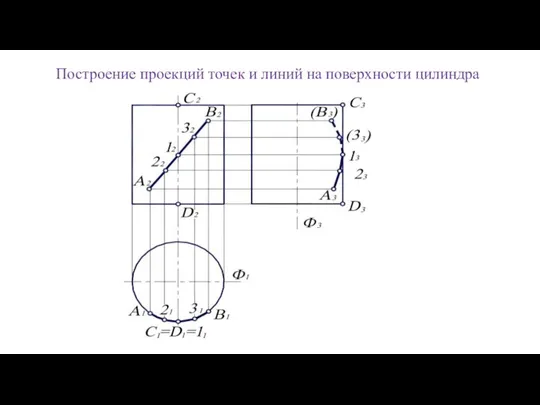
- 58. Недостающие проекции точек, определяются по признаку принадлежности с помощью параллелей проходящих через заданные точки: m' →
- 59. Недостающие проекции точек, определяются по признаку принадлежности с помощью параллелей проходящих через заданные точки: m' →
- 60. Недостающие проекции точек, определяются по признаку принадлежности с помощью параллелей проходящих через заданные точки: m' →
- 61. Недостающие проекции точек, определяются по признаку принадлежности с помощью параллелей проходящих через заданные точки: m' →
- 62. Недостающие проекции точек, определяются по признаку принадлежности с помощью параллелей проходящих через заданные точки: m' →
- 63. Примеры нелинейчатых поверхностей вращения
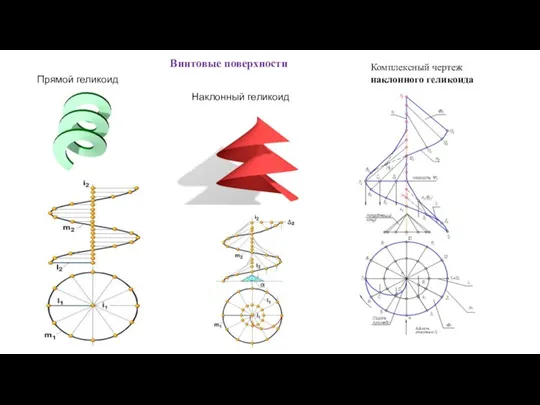
- 64. Винтовые поверхности Прямой геликоид Наклонный геликоид Комплексный чертеж наклонного геликоида
- 65. Винтовые поверхности Прямой геликоид, Винтовой коноид
- 66. Чтобы задать поверхность на чертеже необходимо: 1. Построить проекции определителя. 2. Построить проекции очерковых образующих поверхности
- 67. Точка на поверхности Точка принадлежит поверхности, если она принадлежит линии, принадлежащей этой поверхности. А∈Ф ⇔ А∈
- 68. Линия l, которой должна принадлежать точка, может иметь форму, как прямой линии (образующая), так и окружности
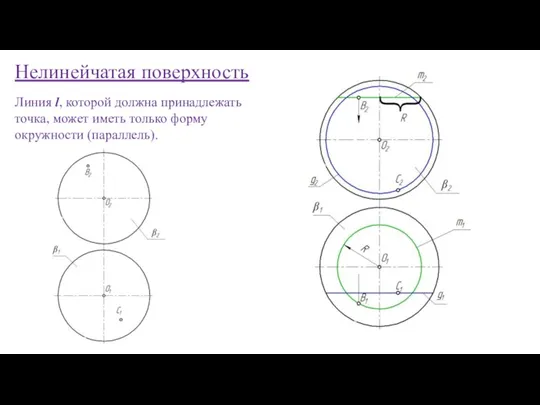
- 69. Нелинейчатая поверхность Линия l, которой должна принадлежать точка, может иметь только форму окружности (параллель).
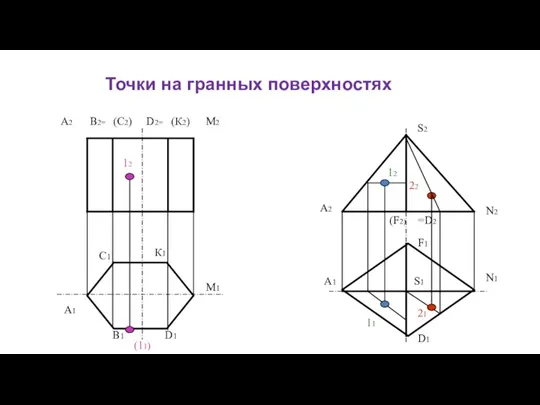
- 70. Точка на гранной поверхности Каждая грань – отсек плоскости. Построение точки на грани сводится к построению
- 71. Линия на поверхности Линия принадлежит поверхности, если все множество ее точек принадлежит этой поверхности. Чтобы построить
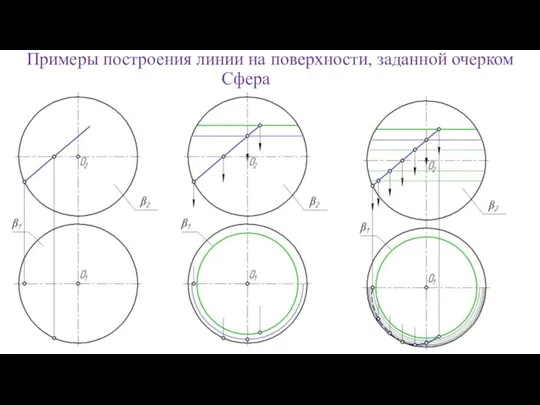
- 72. Сфера Примеры построения линии на поверхности, заданной очерком
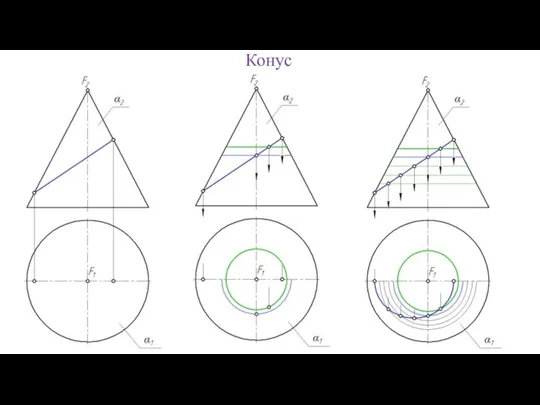
- 73. Конус
- 74. ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ Геометрическая фигура - это любое множество точек. Геометрические фигуры бывают: Плоские (точка, прямая, плоскость
- 75. МНОГОГРАННИКИ Простой многогранной поверхностью называется объединение многоугольников. Многоугольники, составляющие многогранную поверхность, называются гранями, грани пересекаются по
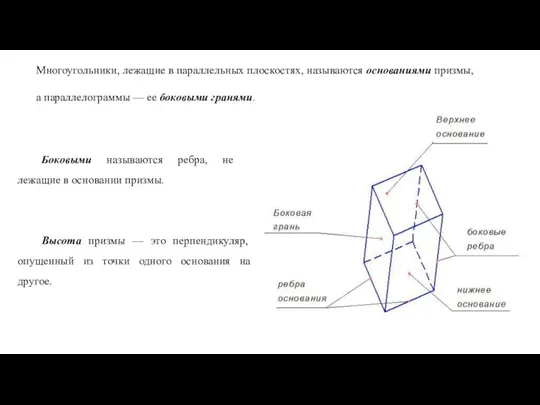
- 76. ПРИЗМА Призма — это многогранник, две грани которого — многоугольники, лежащие в параллельных плоскостях, а остальные
- 77. Многоугольники, лежащие в параллельных плоскостях, называются основаниями призмы, а параллелограммы — ее боковыми гранями. Боковыми называются
- 78. ПИРАМИДА Пирамидой называется многогранник, одна из граней которого — продольный многоугольник, а остальные грани — треугольники,
- 79. Треугольники SАВ, SВС, SАС называются боковыми гранями пирамиды, точка S — вершиной пирамиды, треугольник АВС —
- 80. При пересечении пирамиды плоскостью, параллельной основанию, получается усеченная пирамида.
- 81. ПРОЕЦИРОВАНИЕ ЦИЛИНДРА Цилиндром называется пространственная фигура, полученная при вращении прямоугольника вокруг оси, содержащей его сторону. Прямым
- 82. Боковая поверхность цилиндра – кривая поверхность, называемая цилиндрической. Сторона прямоугольника, параллельная оси, называется образующей цилиндрической поверхности.
- 83. ПРОЕЦИРОВАНИЕ КОНУСА Прямым круговым конусом называется пространственная фигура (множество точек), полученная при вращении прямоугольного треугольника вокруг
- 84. Катет, принадлежащий оси, называется высотой конуса. Второй катет описывает круг, который называется основанием конуса. Гипотенуза называется
- 85. ПРОЕЦИРОВАНИЕ СФЕРЫ Множество всех точек пространства, расстояние от каждой из которых до данной точки не больше
- 86. На сфере выделяют два семейства линий: а) параллели — окружности, получаемые при пересечении сферы плоскостями, перпендикулярными
- 87. 3). Сфера – не линейчатая, не развёртываемая, алгебраическая поверхность второго порядка, получается при вращении окружности или
- 88. 2. Частные виды поверхностей вращения 3). Сфера – не линейчатая, не развёртываемая, алгебраическая поверхность второго порядка,
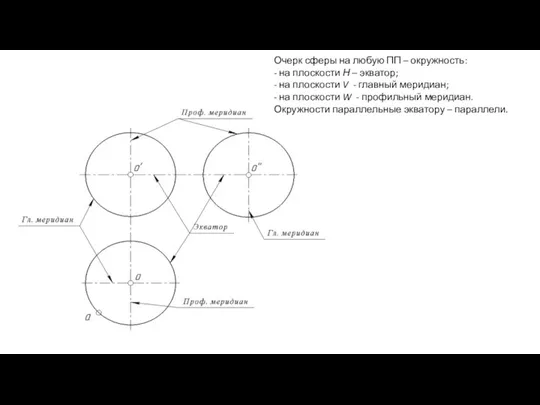
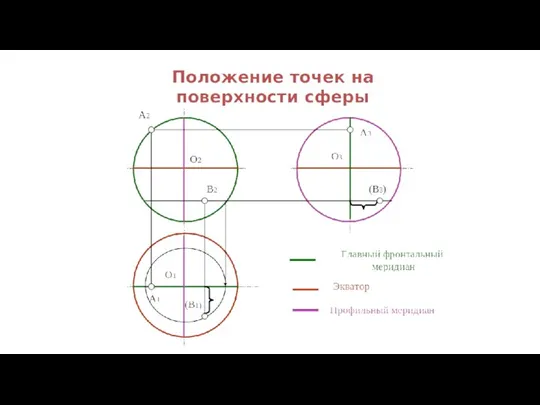
- 89. Очерк сферы на любую ПП – окружность: - на плоскости Н – экватор; - на плоскости
- 90. Видимость сферической поверхности на плоскости Н определяет экватор: точки выше экватора – видны, ниже – не
- 91. a → a', a″ ? Точка А принадлежит экватору на горизонтальной ПП и проекциям экватора на
- 92. b'→ b, b″ ? Точка В принадлежит главному меридиану на фронтальной ПП и проекциям главного меридиана
- 93. b'→ b, b″ ? Точка В принадлежит главному меридиану на фронтальной ПП и проекциям главного меридиана
- 94. c″ → c ,c' ? Точка С принадлежит профильному меридиану на профильной ПП и проекциям профильного
- 95. c″ → c ,c' ? Точка С принадлежит профильному меридиану на профильной ПП и проекциям профильного
- 96. m' →m, m″ ? Точка М принадлежит параллели на фронтальной ПП и проекциям параллели на горизонтальной
- 97. m' →m, m″ ? Точка М принадлежит параллели на фронтальной ПП и проекциям параллели на горизонтальной
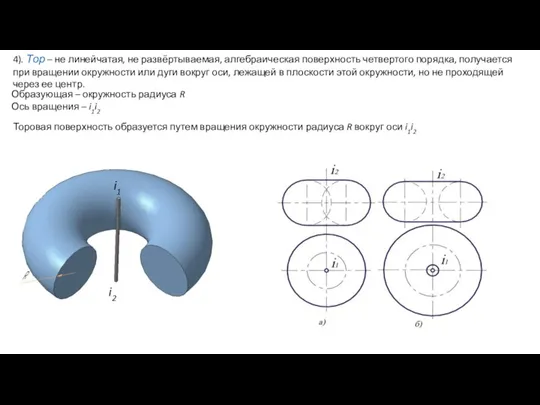
- 98. 4). Тор – не линейчатая, не развёртываемая, алгебраическая поверхность четвертого порядка, получается при вращении окружности или
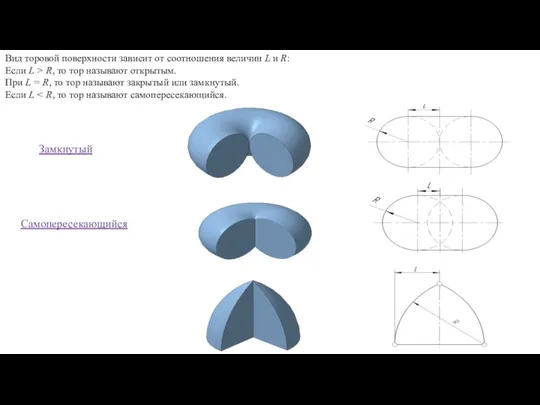
- 99. Вид торовой поверхности зависит от соотношения величин L и R: Если L > R, то тор
- 100. Торовая поверхность образуется путем вращения окружности радиуса R вокруг оси О1О2 так, что центр окружности радиуса
- 101. Горизонтальная проекция торовой поверхности – две концентрические окружности, фронтальная – справа и слева ограничена дугами полуокружности
- 102. Тор имеет две системы круговых сечений: 1). Плоскости, перпендикулярные к оси вращения (Р) образуют две концентрические
- 103. 2). Плоскости, проходящие через ось вращения (Q) пересекает поверхность тора по двум образующим окружностям радиуса R.
- 104. Торовая поверхность образуется путем вращения окружности радиуса R вокруг оси О1О2 так, что центр окружности радиуса
- 105. Цилиндр, конус, сфера
- 106. Построение проекций точек и линий на поверхности цилиндра
- 107. Построение проекций точек и линий на поверхности конуса
- 108. Построение проекций точек и линий на поверхности сферы
- 110. Построение проекций точек и линий на поверхности тора
- 111. Принадлежность точек конической поверхности А2 А1 (В2) В1 (В3) А3
- 112. Точки на гранных поверхностях А1 А2 В2= В1 (С2) С1 D2= D1 (К2) К1 М2 М1
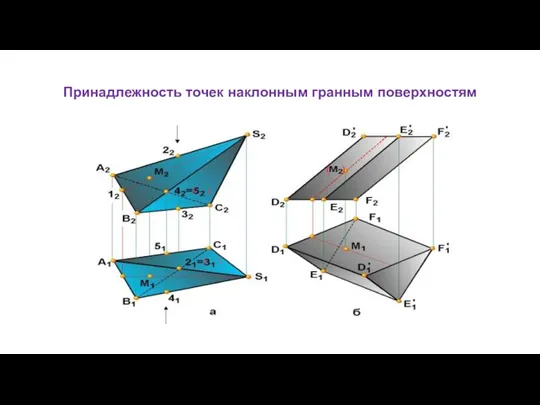
- 113. Принадлежность точек наклонным гранным поверхностям ( ) ( ) ( )
- 114. Пирамида – многогранник, одна из граней которого (основание) есть произвольный многоугольник, остальные n- граней – треугольники,
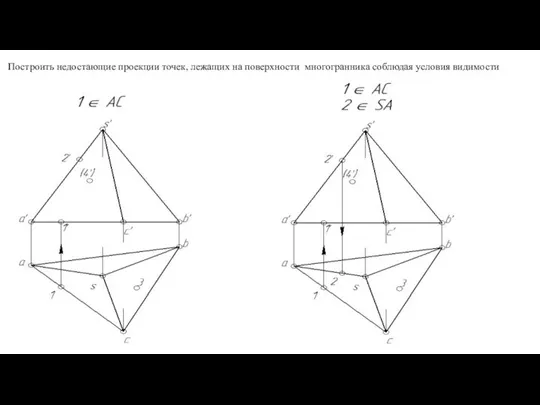
- 115. Построить недостающие проекции точек, лежащих на поверхности многогранника соблюдая условия видимости
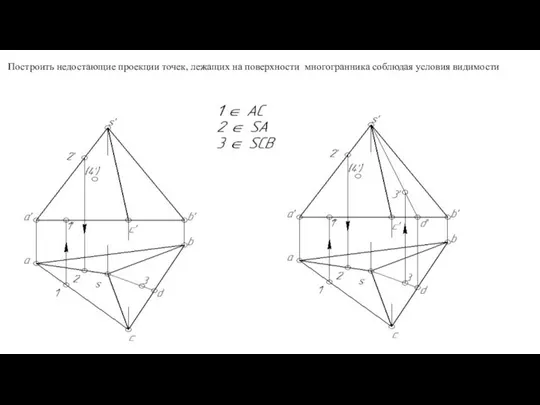
- 116. Построить недостающие проекции точек, лежащих на поверхности многогранника соблюдая условия видимости
- 117. Построить недостающие проекции точек, лежащих на поверхности многогранника соблюдая условия видимости
- 118. Построить недостающие проекции точек, лежащих на поверхности многогранника соблюдая условия видимости
- 120. Скачать презентацию














































































 Сожаление о старом халате.
Сожаление о старом халате. Работники культуры не бездельники ,все они
Работники культуры не бездельники ,все они Словообразование имён существительных
Словообразование имён существительных A X I O M
A X I O M Окаменевшее время Стоунхенджа
Окаменевшее время Стоунхенджа Дебаты – искусство благородного спора
Дебаты – искусство благородного спора Стулья Оримекс
Стулья Оримекс «Программируемые устройства вокруг нас»поисково-исследовательская работа
«Программируемые устройства вокруг нас»поисково-исследовательская работа ВКР: Направления развития ресурсной базы коммерческого банка
ВКР: Направления развития ресурсной базы коммерческого банка Схема передачи информации. Локальные и глобальные компьютерные сети
Схема передачи информации. Локальные и глобальные компьютерные сети Состояние отраслей машиностроения и металлообработки
Состояние отраслей машиностроения и металлообработки Презентация на тему Правовые основы охраны труда
Презентация на тему Правовые основы охраны труда риггеры на биполярных транзисторах. Генераторы линейно-изменяющегося напряжения
риггеры на биполярных транзисторах. Генераторы линейно-изменяющегося напряжения R
R Симметрия в одежде
Симметрия в одежде Роль финансов в эффективном функционировании рыночной экономики
Роль финансов в эффективном функционировании рыночной экономики  LES GENETS D’ORПрезентация организации
LES GENETS D’ORПрезентация организации День народного единства
День народного единства Мое здоровье
Мое здоровье Религиозная толерантность
Религиозная толерантность Создание эскиза театрального героя. 3 класс
Создание эскиза театрального героя. 3 класс СПИД - наиболее опасное инфекционное заболевание.
СПИД - наиболее опасное инфекционное заболевание. Прямые паруса и их бегучий такелаж шлюпа Мирный
Прямые паруса и их бегучий такелаж шлюпа Мирный Отчет по разработке Программы стратегического развития Зеленодольского муниципального района до 2020 года
Отчет по разработке Программы стратегического развития Зеленодольского муниципального района до 2020 года Постановка задачи
Постановка задачи Муниципальное образовательное учреждение средняя общеобразовательная школа № 124 Октябрьского района городского округа город Уф
Муниципальное образовательное учреждение средняя общеобразовательная школа № 124 Октябрьского района городского округа город Уф Потребительские кредиты
Потребительские кредиты Культура России в XIX в
Культура России в XIX в