Применение генетических алгоритмов для генерации тестов к олимпиадным задачам по программированию

Тестирование
Занимает до 50% времени и стоимости разработки ПО
Подлежащие тестированию процессы разнообразны
Автоматизация тестирования позволяет снизить затраты на разработку ПО и увеличить его качество

Олимпиадные задачи
Решения тестируются на определенном наборе тестов
Жесткие ограничения на время работы решения
Простой текстовый формат входных и выходных данных
Автоматическая проверка корректности ответа
Процесс тестирования полностью автоматизирован
Качество проверки зависит от качества набора тестов

Подготовка тестов
Подготовка тестов – творческий процесс, включающий написание неверных и неэффективных решений
Число возможных тестов в большинстве случаев огромно, перебор не представляется возможным
Поиск тестов против наиболее сложных неверных решений – трудная задача
Часто ограничиваются большими случайными тестами, может пострадать качество набора тестов

Генетические алгоритмы как способ поиска тестов
Задачу о поиске тестов против неэффективных решений можно рассматривать как оптимизационную
Параметром оптимизации служит время работы решения на одном тесте, чем оно больше, тем лучше тест
Поиск алгоритма создания хороших тестов можно возложить на генетические алгоритмы

Даны N предметов, каждый с весом WI и стоимостью PI.
Требуется указать, какие из этих предметов нужно выбрать, чтобы их суммарный вес не превзошел W, а суммарная стоимость была бы максимальной
Задача является NP-полной
Разработано множество алгоритмов, решающих эту задачу для больших N (порядка 100 тысяч) за малое время (порядка 1 секунды) для большей части (но не для всех) входных данных
Пример применения:
задача о рюкзаке
Задача: найти трудный тест для конкретного решения.

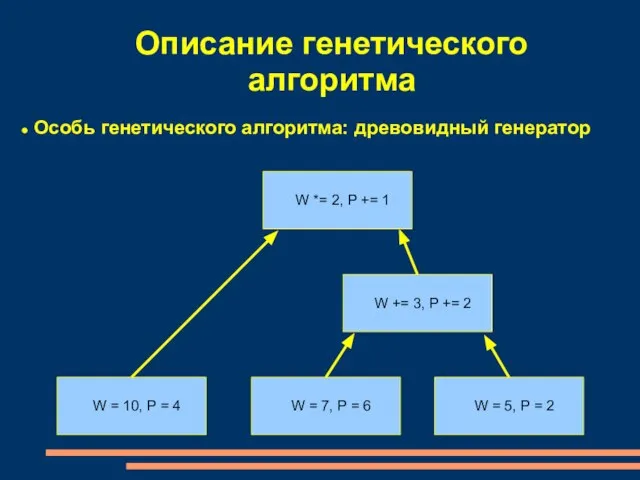
Особь генетического алгоритма: древовидный генератор
Описание генетического алгоритма
W = 10, P = 4
W = 7, P = 6
W = 5, P = 2
W += 3, P += 2
W *= 2, P += 1

Кроссовер – обмен случайными поддеревьями
Мутация – изменение параметров в случайно выбранной вершине
Схема алгоритма – скрещивание с наилучшей особью, затем выбор фиксированного числа наиболее приспособленных особей
Размер поколения – 100 особей
Описание генетического алгоритма

Задача о рюкзаке NP-полна, поэтому у любого ее решения существуют конфигурации входных данных, трудные для обработки
Поддерево генератора теста представляет собой описание некоторой конфигурации части теста
Поддерево будет сохраняться в поколении, если генерируемая им конфигурация является трудной для алгоритма
Обоснование применимости генетического алгоритма

Задача: N = 10, 0 <= W,P <= 2128
Ограничение по времени: 4 секунды
За 30 минут генетическим алгоритмом найден тест, на котором решение работает больше 4 секунд
Генерация тестов случайным образом в соответствии с шаблоном, известным как самый сложный случай для данного алгоритма, в течение 2 часов не привела к подобному результату (максимальное достигнутое время работы – 2 секунды)‏
Результаты работы