Применение теоремы Пифагора

«Геометрия владеет двумя сокровищами, одно из них - это теорема Пифагора»
Иоганн Кеплер

Цель данной работы:
исследовать теорему Пифагора и выяснить области применения теоремы. Задачи:
Изучить некоторые исторические сведения о Пифагоре;
Рассмотреть историю открытия теоремы Пифагора;
Собрать информацию о практическом применении теоремы в различных источниках и определить области ее применения;
Показать применение теоремы Пифагора при решении различных задач;
Оформить наработанный материал.

Знаменитый греческий
философ и математик
Пифагор Самосский,
именем которого названа
теорема, жил около 2,5
тысяч лет тому назад.

с2 =а2 + b2
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов

Задача индийского математика XII века Бхаскары
"На берегу реки рос тополь одинокий. Вдруг ветра порыв его ствол надломал.
Бедный тополь упал. И угол прямой
С теченьем реки его ствол составлял.
Запомни теперь, что в этом месте река
В четыре лишь фута была широка
Верхушка склонилась у края реки.
Осталось три фута всего от ствола,
Прошу тебя, скоро теперь мне скажи:
У тополя как велика высота?"

32+42=х2
х2=25
х=5 ( футов) длина отломленной части ствола
3+5=8 (футов) высота тополя

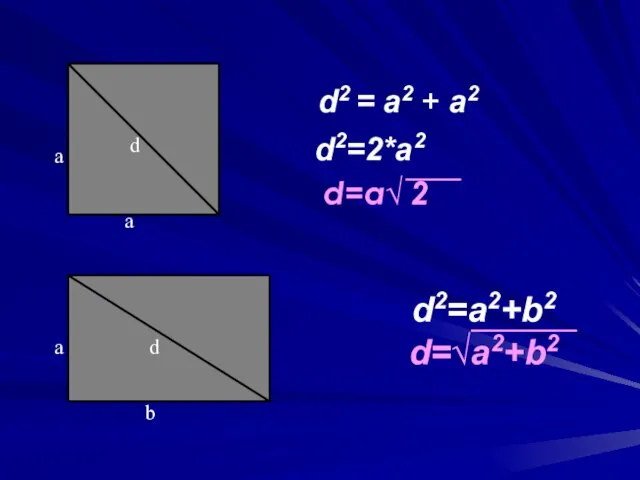
Теорема Пифагора для вычисления длин отрезков некоторых фигур.

d2 = a2 + a2
d2=2*a2
d=a√ 2
d2=a2+b2 d=√a2+b2

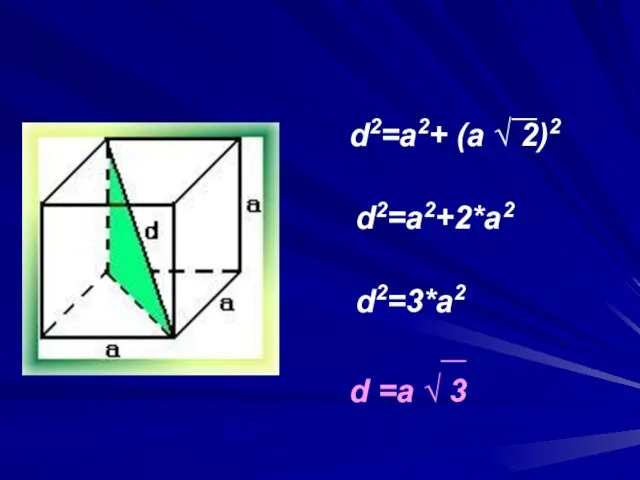
d2=a2+ (a √ 2)2
d2=a2+2*a2
d2=3*a2
d =a √ 3

Применение теоремы Пифагора на практике

Пример 1.
В зданиях романского и готического стиля верхние части окон расчленяются каменными рёбрами, которые не только играют роль орнамента, но и способствуют прочности окон.

Если b обозначает ширину окна, то радиусы полуокружностей будут равны R=b/2 и r =b/4. Радиус p внутренней окружности можно вычислить из прямоугольного треугольника, изображённого на рисунке цветом
Гипотенуза этого треугольника, проходящая через точку касания окружностей, равна b/4+ p, один катет равен b/4, а другой b/2- p.
По теореме Пифагора имеем:
(b/4+ p)2=(b/4)2+(b/2- p)2
Выполнив преобразования , получим :
p=b/6
b

Пример 2.
В доме задумано построить двускатную крышу . Какой длины должны быть стропила, если изготовлены балки определенной длины.

Высота чердака h=2м, длина стороны дома b=6м
длина стропил L= √ 22+32=√13≈3,6 м

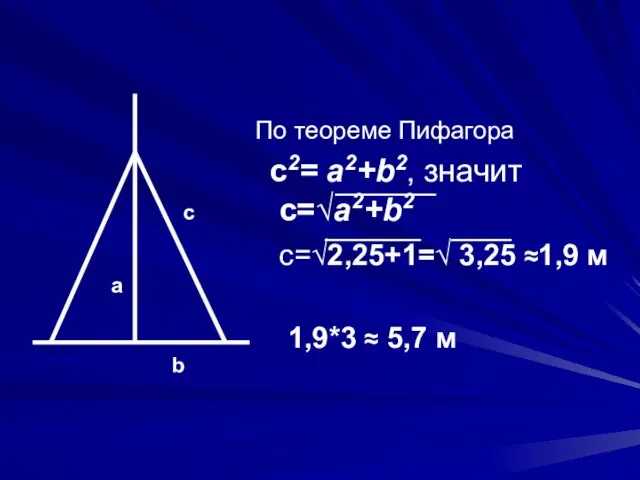
Пример 3.
Закрепить трубу на школьной котельной угольниками. Один конец угольника должен крепиться на высоте 1,5м, другой на земле на расстоянии 1 м от трубы. Определить сколько метров угольника понадобится для того, чтобы закрепить трубу.

По теореме Пифагора
с2= a2+b2, значит c=√a2+b2
с=√2,25+1=√ 3,25 ≈1,9 м
1,9*3 ≈ 5,7 м

Пример 4.
Мобильная связь
Какую наименьшую высоту должна иметь вышка мобильной связи, поставленная в селе Кулунда, чтобы близлежащие села попали в зону связи?

Решение: Пусть AB= x км, радиус зоны связи ВС=31 км, радиус Земли 6380 км
Применив теорему Пифагора, получу уравнение
(х+6380)2=312+63802;
х2+12760х- 961=0;
D=162817600+3844=162821444, √D≈12760,150;
х≈75 м