Слайд 2Эпиграф
«Кто смолоду делает и
думает сам,
Тот становится потом надежнее,

крепче, умнее».
В. Шукшин
Слайд 3 Представьте в виде произведения разность
sin 0,3π – cos 0,6π

Слайд 4Восстановите запись:
а)sin 40º+ sin …º = …sin 28º • …12º,
б)cos …º -

cos 74º = - 2 sin …º sin(-14º)
Слайд 5
На «5»
1. Зная, что sin α + cos α = 1,4,

найдите: sin α • cos α.
2. Используя формулы сложения, вычислите: √2/2+cos(- 75º).
3. Упростите выражение: 3соs (π/2 + α) – 4sin (α - π)
На «4»
1. Используя формулы сложения, вычислите: cos (-75º).
2. Известно, что соs α = -5/13 и α – угол II четверти.
Найдите sin 2α.
3. Найдите значение выражения: sin 150º + 2cos180º.
На «3»
1. Упростите выражение: 1 + cos 2α - sin2α.
2. Вычислите: 4sin (- 30º) + 2соs 60º.
3. Зная, что sin α = 0,4, найдите значение выражения: 1 – соs 2 α.
Слайд 6На «5»
1. (sin α + cos α)^ = 1,4^;
sin α•cos

α=0,48 .
2. + соs (-75º) =
3. – 3sinα + 4 sin α = sin α.





 Тема: «Спортивные игры зимой»
Тема: «Спортивные игры зимой» Список детей на получение кроватей и полотенец
Список детей на получение кроватей и полотенец Тепловые двигатели. Паровая турбина.
Тепловые двигатели. Паровая турбина. Система образования в Англии
Система образования в Англии Геометрические паркеты
Геометрические паркеты Подходы к системному целеполаганию. Лекция 2
Подходы к системному целеполаганию. Лекция 2 Конституция РФ
Конституция РФ Проект "Задачи на смеси и сплавы"
Проект "Задачи на смеси и сплавы" Раздел #. Дизайн интерьера
Раздел #. Дизайн интерьера Основы научных исследований
Основы научных исследований 000834aa-f5be4922
000834aa-f5be4922 Погружение
Погружение Невербальное общение
Невербальное общение Однородность керамзита
Однородность керамзита Презентация на тему Длина и меры ее измерения
Презентация на тему Длина и меры ее измерения Презентация на тему Экономика как наука
Презентация на тему Экономика как наука Кофемашина Yamaguchi CoffeeMann
Кофемашина Yamaguchi CoffeeMann Танковая викторина
Танковая викторина Петр Петрович Семёнов-Тян-Шанский
Петр Петрович Семёнов-Тян-Шанский Александр
Александр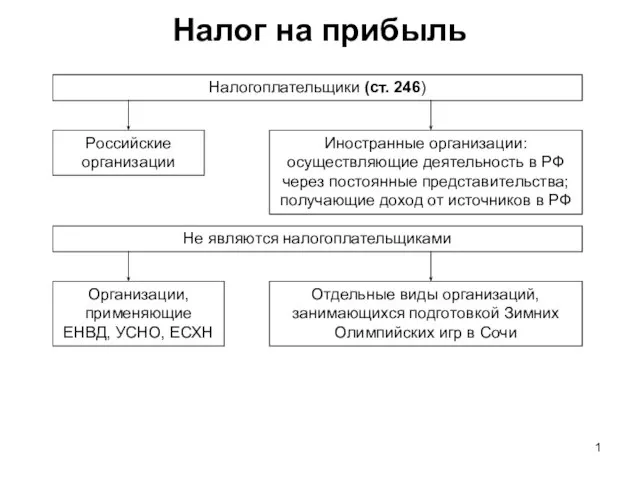 Налог на прибыль
Налог на прибыль SPORTS in Our Life
SPORTS in Our Life  Аудирование —цель и средство обучения
Аудирование —цель и средство обучения Отношения мужчины и женщины. Женская психология
Отношения мужчины и женщины. Женская психология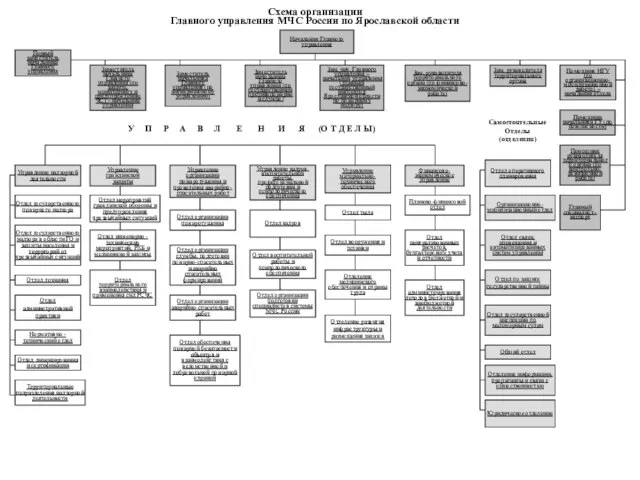 Схема организации Главного управления МЧС России по Ярославской области
Схема организации Главного управления МЧС России по Ярославской области Презентация на тему Афанасий Афанасьевич Фет (4 класс)
Презентация на тему Афанасий Афанасьевич Фет (4 класс) муниципальное образовательное учреждениеОбходская основная общеобразовательная школаУренского муниципального районаНижегор
муниципальное образовательное учреждениеОбходская основная общеобразовательная школаУренского муниципального районаНижегор куликовская битва
куликовская битва