ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО КУРСУ ФИЗИЧЕСКИЕ ОСНОВЫ ЭКСПЕРИМЕНТАЛЬНЫХ МЕТОДОВ ИССЛЕДОВАНИЯ РЕАЛЬНОЙ СТРУКТУРЫ КРИСТАЛЛОВ
Содержание
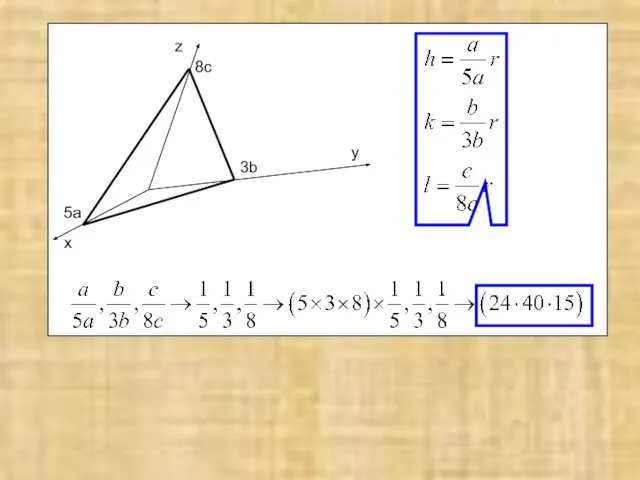
- 2. №1. Плоскость отсекает на осях координат отрезки 5, 3, 8 соответственно в параметрах элементарной ячейки a,b,c.
- 3. x y z 5a 3b 8c
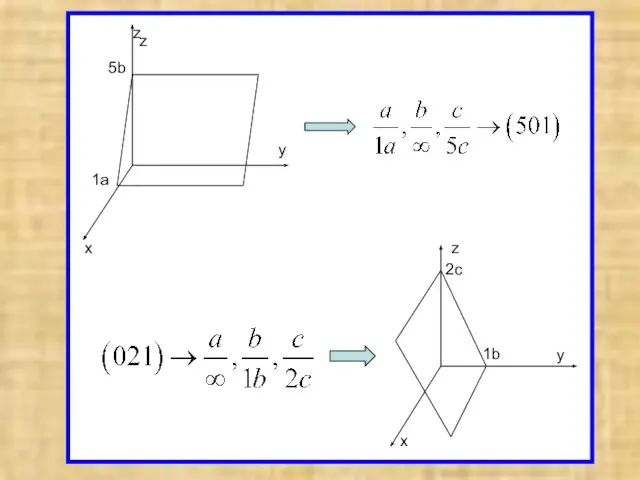
- 4. x y z 1a 5b z x y z 1b 2c
- 5. Обратная решетка. Её свойства Здесь h,k,l – тоже целые числа Здесь m,m,p–целые числа Например, равенство (a,b*)=(c,b*)=0
- 6. Последние три равенства можно переписать так Однако из векторной алгебры известно, что смешанное произведения трех векторов
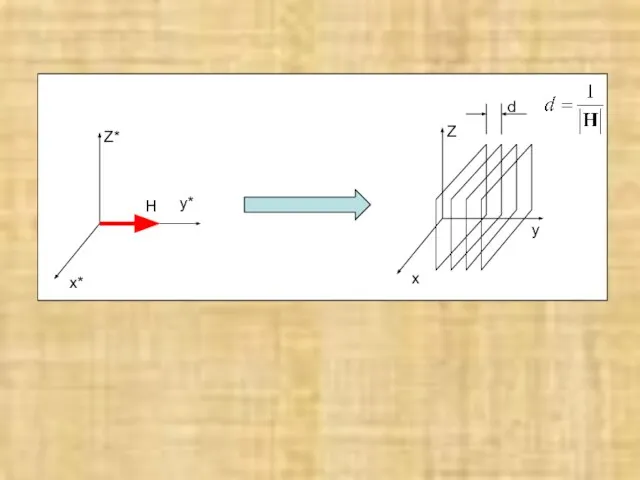
- 7. №2. Чему в прямой решетке соответствует точка в обратной решетке
- 8. x* y* Z* H x Z d y
- 9. №3. Показать, что вектор обратной решетки Hhkl перпендикулярен плоскости прямой решетки с индексами (hkl).
- 10. Введем в обратной решетке вектор Этот вектор обладает чрезвычайно важным свойством – он всегда перпендикулярен плоскостям
- 11. №4. Показать, что модуль вектора обратной решетки равен обратной величине межплоскостного расстояния для плоскосей с индексами
- 12. Другим важнейшим свойством вектора H является то, что его модуль всегда равен обратной величине межплоскостного расстояния
- 13. №5. Рассчитать структурную амплитуду для гранецентрированной кубической решетки. Определить закон погасания рефлексов для этой структуры.
- 14. Для гранецентрированной кубической решетки базис записывается, как Если положить, что все атомы, входящие в кристаллическую решетку,
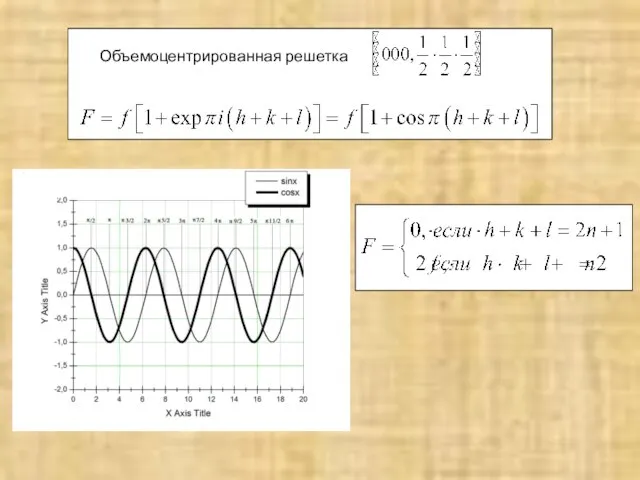
- 16. №6. Рассчитать структурную амплитуду для объемоцентрированной кубической решетки. Определить закон погасания рефлексов для этой структуры.
- 17. Объемоцентрированная решетка
- 18. №7. Рассчитать структурную амплитуду, структурный фактор и определить законы погасаний для решетки алмаза. Решетка алмаза это
- 19. [[000; 1/2,1/2,0; 1/2,0,1/2; 0,1/2,1/2; 1/4,1/4,1/4; 3/4,3/4,1/4; 3/4,1/4,3/4; 1/4,3/4,3/4]] -гранецентрированная решетка
- 20. №8 На щель шириной a падает плоская волна. Рассчитать распределение излучения за этой щелью. (Дифракция на
- 22. f(x) 1 x Запишем выражение, описывающее щель, в виде функции Фурье-образ такой функции будет описываться Вспоминая,
- 23. №9. Определить число атомов в элементарной ячейке железа, кристаллизующегося в кубической системе; ребро куба а=2,87Å, атомный
- 24. Применяя формулу плотности к элементарной ячейке, находим т.е. на элементарную ячейку приходится 2 атома. Здесь A
- 25. №10. Рассчитать необходимую ширину щели коллиматора для выделения Кα1 линии в методе Ланга. Исследуемый кристалл -
- 26. Запишем условия Брэгга для этих длин волн Ширина щели, формирующая пучок, определяет величину расходимости падающего на
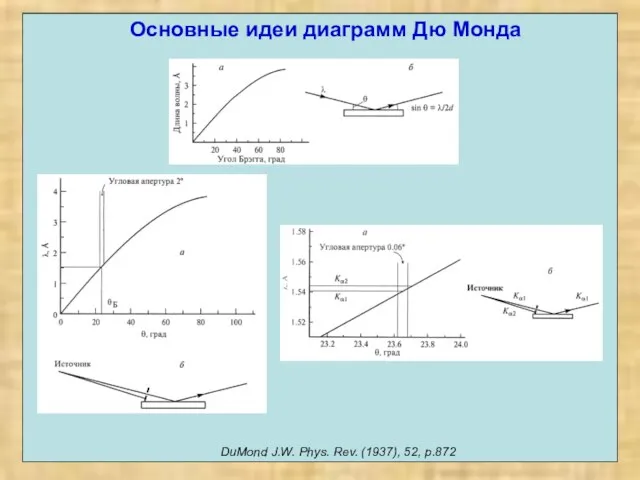
- 27. Основные идеи диаграмм Дю Монда DuMond J.W. Phys. Rev. (1937), 52, p.872
- 28. №11. Определить экстинкционную длину для отражения (220) кремния (излучения MoKα1 и CuKα1). Фурье-компонента поляризуемости для этого
- 29. Экстинкционная длина определяется соотношением где и - Фурье–компоненты поляризуемости кристалла для данной системы плоскостей. Если кристалл
- 30. №12. Оценить толщину кристалла кремния, при которой соотношение амплитуд нормальной и аномальной волн для симметричного отражения
- 31. Величины поглощения для нормальной и аномальной волн задаются соотношением Знак плюс относится к поглощению нормальной моды.
- 32. №13. Определить все элементы симметрии куба. Изобразить это на стереографической проекции
- 34. Скачать презентацию












![[[000; 1/2,1/2,0; 1/2,0,1/2; 0,1/2,1/2; 1/4,1/4,1/4; 3/4,3/4,1/4; 3/4,1/4,3/4; 1/4,3/4,3/4]] -гранецентрированная решетка](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/410181/slide-18.jpg)

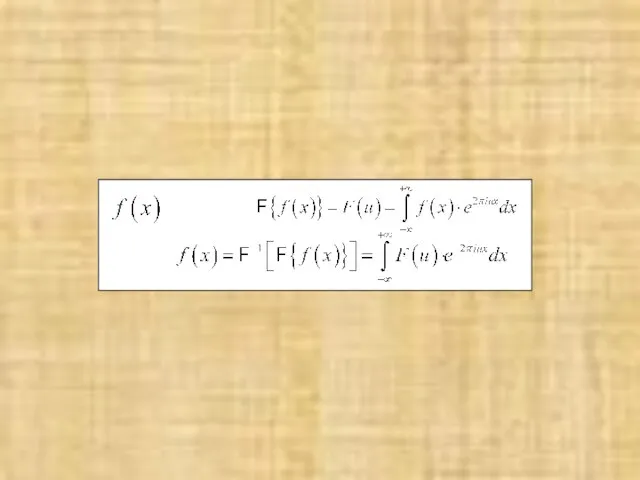










 Специалист по рекламе. Что будет на курсе
Специалист по рекламе. Что будет на курсе Золотое сечение в городе Елец
Золотое сечение в городе Елец Презентация на тему: Поэтическая система А.А.Фета
Презентация на тему: Поэтическая система А.А.Фета Бытовая швейная машина
Бытовая швейная машина Уход за одеждой
Уход за одеждой Герои-космонавты
Герои-космонавты Моя будущая профессия - учитель
Моя будущая профессия - учитель Почему ветер поднимает листья?
Почему ветер поднимает листья? Презентация на тему Мобильные телефоны как фактор риска здоровью учащихся
Презентация на тему Мобильные телефоны как фактор риска здоровью учащихся Презентація
Презентація Методология менеджмента сетей науки и образования. Концептуальный подход.
Методология менеджмента сетей науки и образования. Концептуальный подход. Ордена Великой Отечественной войны
Ордена Великой Отечественной войны Презентация на тему Клетки и ткани человека
Презентация на тему Клетки и ткани человека Орфография
Орфография Русская матрешка
Русская матрешка Презентация на тему Анна Ахматова Реквием
Презентация на тему Анна Ахматова Реквием Устный счет
Устный счет День спортивного журналиста
День спортивного журналиста АСЕПТИКА И АНТИСЕПТИКА
АСЕПТИКА И АНТИСЕПТИКА Предупреждение противоправного поведения молодёжи
Предупреждение противоправного поведения молодёжи Презентация на тему Формирование здоровых детско-родительских отношений
Презентация на тему Формирование здоровых детско-родительских отношений  Япония во второй половине XX века
Япония во второй половине XX века Презентация на тему М.Ю. Лермонтов «Дары Терека»
Презентация на тему М.Ю. Лермонтов «Дары Терека» Алгоритм получения сертификата 2014
Алгоритм получения сертификата 2014 Электромагнитные колебания (11 класс)
Электромагнитные колебания (11 класс) Юрий Визбор
Юрий Визбор Одежда мусульманина
Одежда мусульманина Категория состояния. Употребление в предложении
Категория состояния. Употребление в предложении