Принцип Кавальери

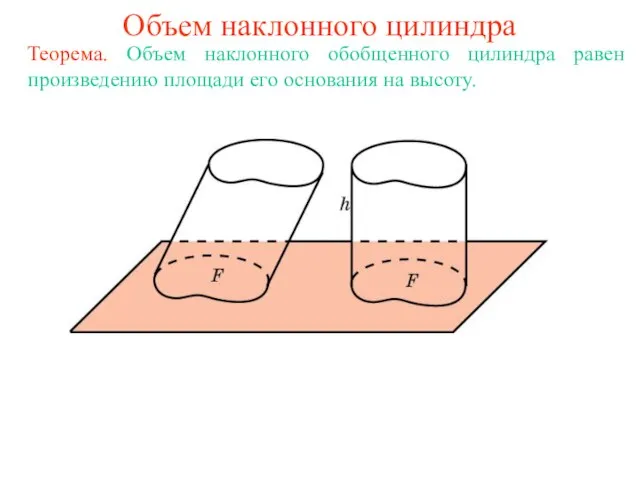
Объем наклонного цилиндра
Теорема. Объем наклонного обобщенного цилиндра равен произведению площади его основания на высоту.

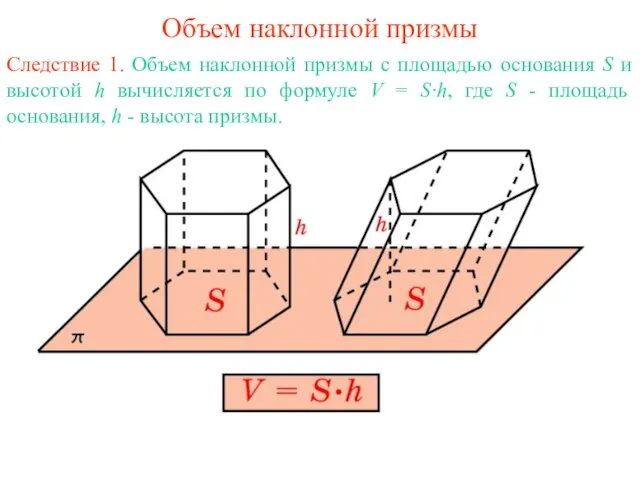
Объем наклонной призмы
Следствие 1. Объем наклонной призмы с площадью основания S и высотой h вычисляется по формуле V = S·h, где S - площадь основания, h - высота призмы.

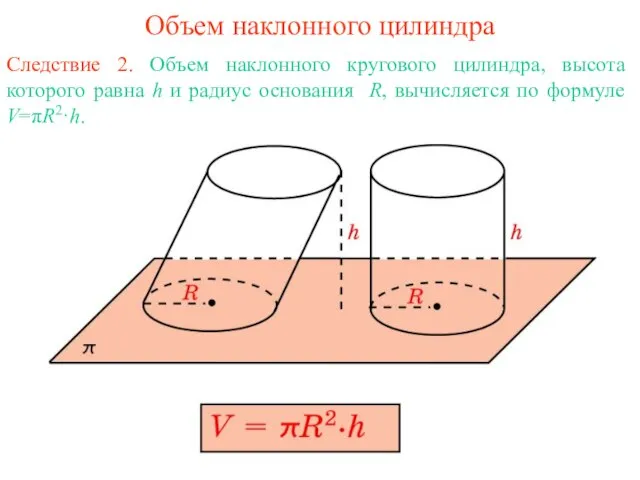
Объем наклонного цилиндра
Следствие 2. Объем наклонного кругового цилиндра, высота которого равна h и ради­ус основания R, вычисляется по формуле V=πR2·h.

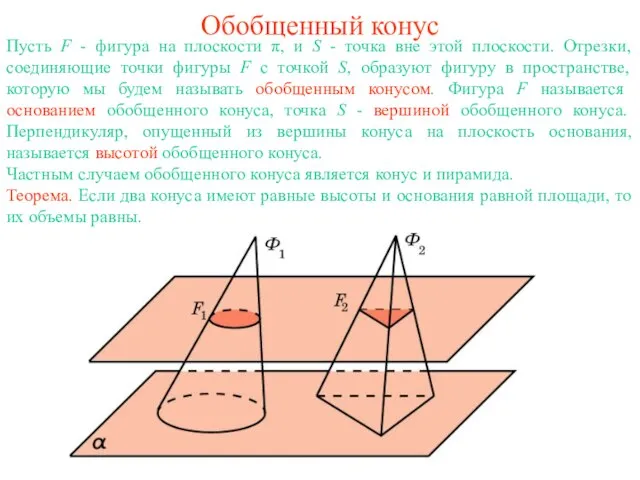
Обобщенный конус
Пусть F - фигура на плоскости π, и S - точка вне этой плоскости. Отрезки, соединяющие точки фигуры F с точкой S, образуют фигуру в пространстве, которую мы будем называть обобщенным конусом. Фигура F называется основанием обобщенного конуса, точка S - вершиной обобщенного конуса. Перпендикуляр, опущенный из вершины конуса на плоскость основания, называется высотой обобщенного конуса.
Частным случаем обобщенного конуса является конус и пирамида.
Теорема. Если два конуса имеют равные высоты и основания равной площади, то их объемы равны.

Упражнение 1
Верно ли, что две пирамиды, имеющие общее основание и вершины, расположенные в плоскости, параллельной основанию, равновелики?
Ответ: Да.

Упражнение 2
Верно ли, что любая плоскость, проходящая через центры оснований наклонного кругового цилиндра, делит его на равновеликие части?
Ответ: Да.

Упражнение 3
В основаниях наклонной призмы квадраты. Верно ли, что любая плоскость, проходящая через центры квадратов, делит призму на две равновеликие части?
Ответ: Да.

Упражнение 4
Два цилиндра имеют равные высоты, а площадь основания одного в два раза больше площади основания другого. Как относятся их объемы?
Ответ: 2:1.

Упражнение 5
Верно ли, что любая плоскость, проходящая через вершину и центр основания наклонного кругового конуса, делит его на равновеликие части?
Ответ: Да.

Упражнение 6
В основании пирамиды квадрат. Верно ли, что любая плоскость, проходящая через вершину пирамиды и центр основания, делит пирамиду на две равновеликие части?
Ответ: Да.

Упражнение 7
Два конуса имеют равные высоты, а площадь основания одного в три раза больше площади основания другого. Как относятся их объемы?
Ответ: 3:1.

Упражнение 8
Найдите объем наклонной призмы, площадь основания ко­торой равна S, а боковое ребро b наклонено к плоскости основания под углом φ.
Ответ: V = S⋅b⋅sin ϕ.

Упражнение 9
Стороны основания параллелепипеда равны 6 дм и 8 дм, угол меж­ду ними 45°. Боковое ребро равно 7 дм и наклонено к плоскости основания под углом 45°. Найдите объем параллелепипеда.
Ответ: 168 дм3.

Упражнение 10
Найдите объем наклонного параллелепипеда, у которого площадь основания равна Q, а боковое ребро, равное b, наклонено к плоскости основания под углом φ.
Ответ: Q⋅b⋅sin ϕ.

Упражнение 11
Найдите объем наклонного кругового цилиндра, радиус основания которого равен R и образующая b наклонена к плоскости основания под углом φ.
Ответ: π⋅R2⋅b⋅sin ϕ.

Упражнение 12
Основанием наклонного параллелепипеда служит квадрат, сторона которого равна 1 м. Одно из боковых ребер образует с каждой прилежащей стороной основания угол в 60° и равно 2 м. Найдите объем параллелепипеда.
Ответ: м3.

Упражнение 13
Основанием наклонной призмы является равносторонний треугольник со стороной a. Одна из боковых граней перпендикулярна основанию и является ромбом, у которого меньшая диагональ равна d. Найдите объем призмы.

Упражнение 14
Боковые ребра наклонной треугольной призмы равны 15 см, а расстояния между ними равны 26 см, 25 см и 17 см. Определите объем призмы.
Ответ: 3060 см3.