Пирамида

пирамида
Составила учитель математики
МОУ «Гимназия им. Горького А.М.»:
Фабер Г.Н.

Информационно-коммуникативную компетентность учащихся:
учить, искать и находить нужные сведения в огромных информационных массивах, в том числе в Интернете;
развивать способность структурировать и обрабатывать данные в зависимости от конкретной задачи;
учить применять полученные навыки и информацию в организации процесса собственного труда для плодотворной работы в группе и творческом коллективе
Цели урока – формировать

содержание
определение пирамиды
виды пирамид
правильные пирамиды
построение правильной пирамиды
свойства правильной пирамиды
площадь поверхностиплощадь поверхности площадь поверхности пирамиды

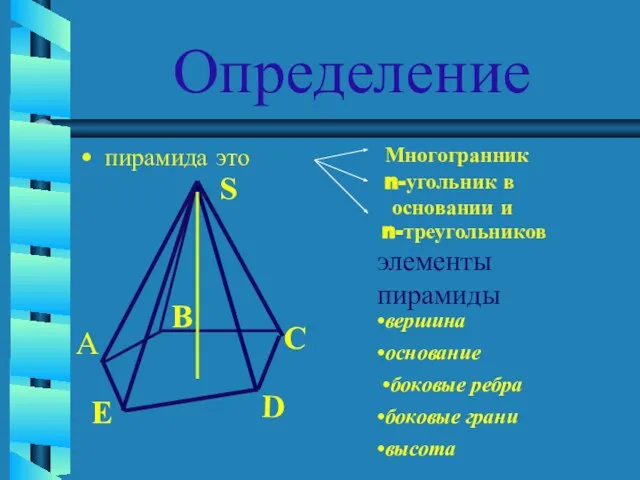
Определение
пирамида это
n-треугольников
элементы пирамиды
S
B
C
D
E
А
вершина
Многогранник
n-угольник в
основании и
основание
боковые грани
боковые ребра
высота

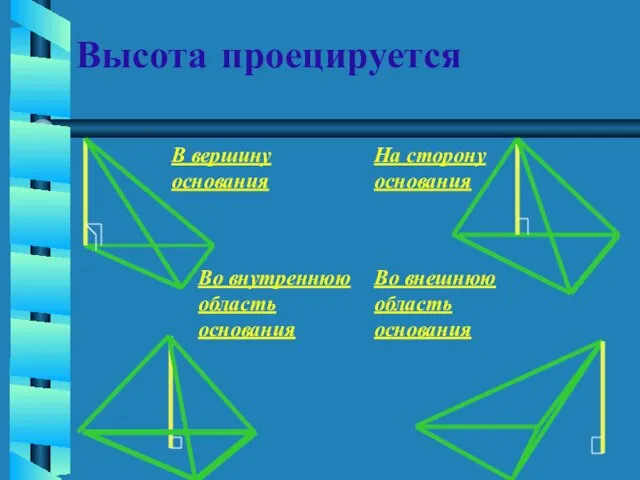
Высота проецируется
В вершину основания
На сторону основания
Во внутреннюю область основания
Во внешнюю область основания

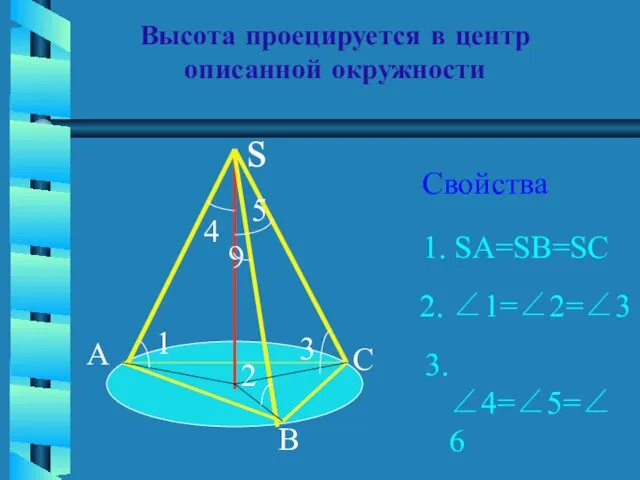
Высота проецируется в центр описанной окружности
Свойства
s
A
B
C
1
2
3
6
4
5
1. SA=SB=SC
2. ∠1=∠2=∠3
3. ∠4=∠5=∠6

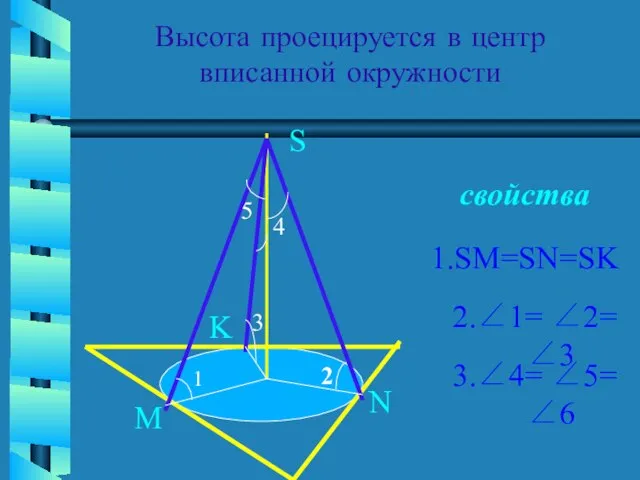
Высота проецируется в центр вписанной окружности
свойства
S
M
N
K
1
2
3
4
5
1.SM=SN=SK
2.∠1= ∠2= ∠3
3.∠4= ∠5= ∠6

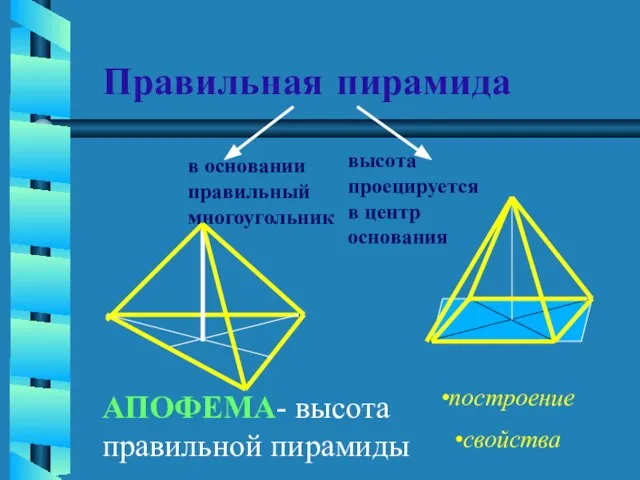
Правильная пирамида
в основании правильный многоугольник
высота проецируется в центр основания
построение
свойства
АПОФЕМА- высота правильной пирамиды

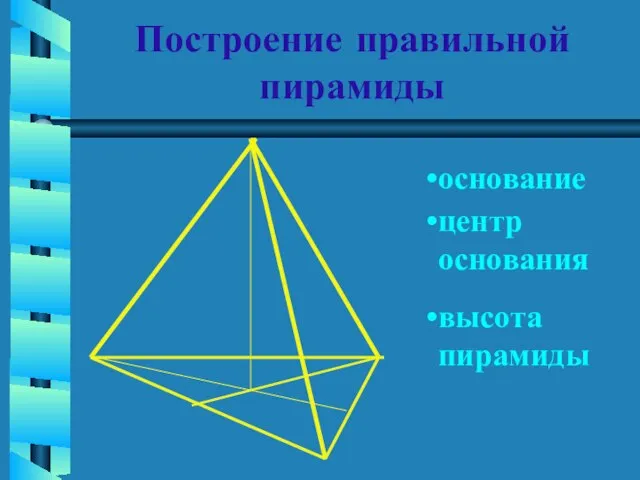
Построение правильной пирамиды
высота пирамиды
основание
центр основания

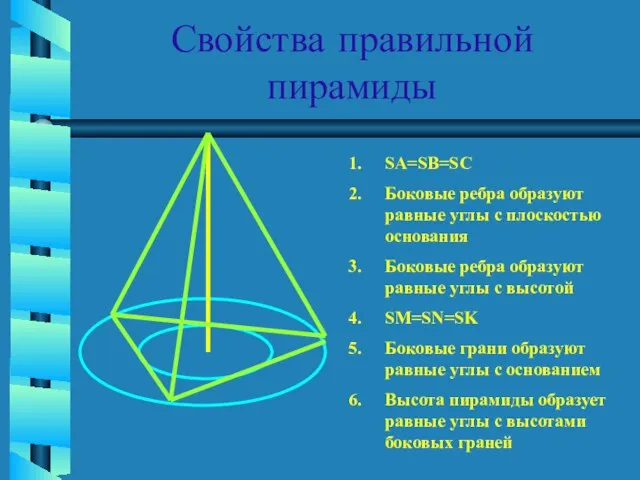
Свойства правильной пирамиды
SA=SB=SC
Боковые ребра образуют равные углы с плоскостью основания
Боковые ребра образуют равные углы с высотой
SM=SN=SK
Боковые грани образуют равные углы с основанием
Высота пирамиды образует равные углы с высотами боковых граней

Площадь поверхности пирамиды
Sпол.=Sбок.+Sосн.

Пирамиды вокруг нас
(Дом. задан. уч-ся)

Пирамиды вокруг нас
«В немой дали застыли пирамиды
фараонов, саркофаги древней были.
Величавые как вечность, молчаливые как смерть»
Михай Эминеску

Рабочие группы
Математики
Историки
Исследователи мировой системы пирамид
Исследователи свойств пирамид
Архитекторы

Математическая точка зрения
Евклид пирамиду определяет как телесную фигуру, ограниченную плоскостями, которые от одной плоскости сходятся к одной точке.
Герон предложил следующее определение пирамиды: «Это фигура, ограниченная треугольниками, сходящимися в одной точке и основанием которой служит многоугольник».

Математическая точка зрения
Адриен Мари Лежандр в своём труде «Элементы геометрии» в 1794 г. даёт определение: «Пирамида – телесная фигура, образованная треугольниками, сходящимися в одной точке и заканчивающаяся на различных сторонах плоского основания».
В учебнике XIX в. Фигурировало определение: «пирамида – телесный угол, пересечённый плоскостью».

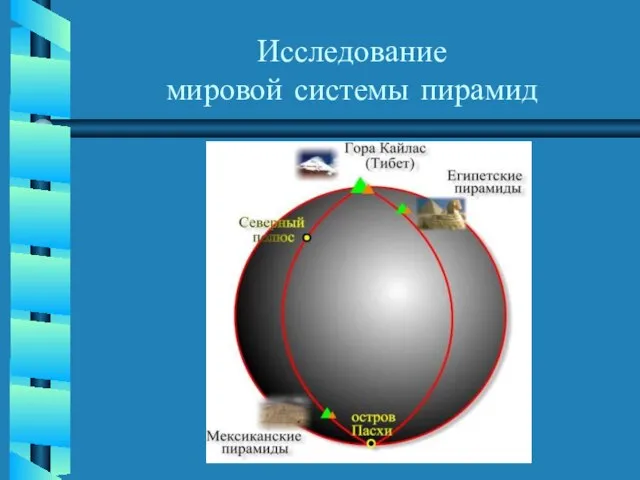
ЕГИПЕТСКИЕ ПИРАМИДЫ
Исследование
мировой системы пирамид
Исследование
мировой системы пирамид

Учебник элементарной геометрии А. Киселева, 1907 г.

Историческая точка зрения
ПИРАМИДА, монументальное сооружение, имеющее геометрическую форму пирамиды (иногда ступенчатую или башнеобразную). Пирамидами называют гробницы древне-египетских фараонов
3 – 2-го тыс. до н. э., а также постаменты храмов в Центральной и Южной Америке, связанные с космологическими культами.
Терра-Лексикон: Иллюстрированный
энциклопедический словарь, 1998

Историческая точка зрения
Мексиканская пирамида Солнца
Ступенчатая пирамида в Египте

АЛЕКСАНДРОВСКИЙ МАЯК
Исследование
мировой системы пирамид

Исследование
мировой системы пирамид
Гора Кайлас на Тибете

Исследование
мировой системы пирамид

Золотое сечение
ЗОЛОТОЕ СЕЧЕНИЕ, деление отрезка АС на две части таким образом, что большая его часть АВ относится к меньшей ВС так, как весь отрезок АС относится к АВ. Приближённо это отношение равно 5/3, точнее 8/5, 13/8 и т. д. Принципы З. с. используются в архитектуре. Термин «З. с.» ввёл Леонардо да Винчи (кон. 15 в.).

Исследование свойств пирамид
При постройке египетских пирамид было установлено, что квадрат, построенный на высоте пирамиды, в точности равен площади каждого из боковых треугольников. Это подтверждается новейшими измерениями.
Если сторону основания пирамиды разделить на точную длину года – 365,2422 суток, то получается 10-миллионная доля земной полуоси с большой точностью.

Исследование свойств пирамид
Мы знаем, что отношение между длиной окружности и её диаметром есть постоянная величина, хорошо известная современным математикам, школьникам – это число π = 3,1416… Но если сложить четыре стороны основания пирамиды Хеопса, мы получим 931,22 м. Разделив это число на удвоенную высоту пирамиды (2*148,208), мы получим 3,1416…, то есть число π.

Пирамиды в архитектуре
Торговый центр в Илинге, Лондон

Задание группе «Математиков»
Изучить пирамиду как геометрическое тело.
Найти определения пирамиды, которые были сформулированы древними учёными.
Сравнить современные трактовки с древними.

Задание группе «Историков»
Найти материалы о первых пирамидах.
Изучить древние пирамиды с математической точки зрения.
Сформулировать вывод о значимости пирамид с исторической и математической точек зрения.

Задание группе «Исследователей мировой системы пирамид»
Установить наличие мест расположения пирамид на Земле.
Установить связи между местами расположения пирамид.
Сформулировать вывод о расположении пирамид на Земле.