– боковые грани
Отрезки А1В1, А2В2…АnBn – боковые ребра призмы
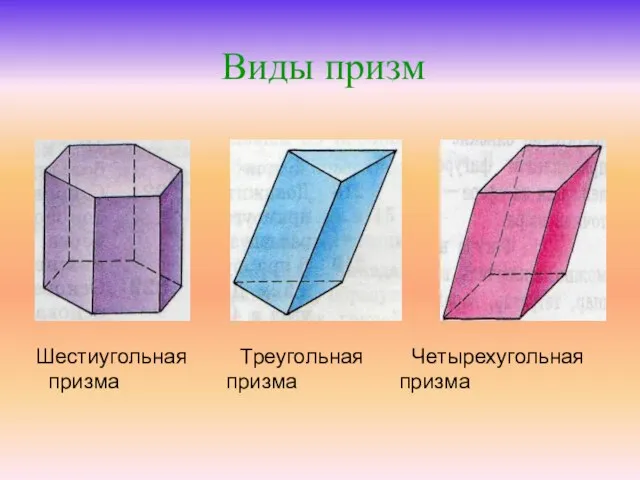
Призмой называется многогранник, у которого две грани ( основания ) лежат в параллельных плоскостях, а все ребра вне этих граней параллельны между собой.
Грани призмы, отличные от оснований, называются боковыми гранями , а их ребра называются боковыми ребрами . Все боковые ребра равны между собой как параллельные отрезки, ограниченные двумя параллельными плоскостями. Все боковые грани призмы являются параллелограммами. Соответствующие стороны оснований призмы равны и параллельны. Поэтому в основаниях лежат равные многоугольники.
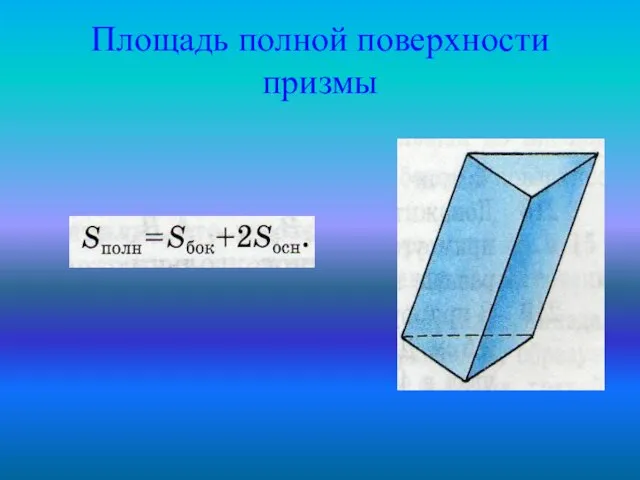
Поверхность призмы состоит из двух оснований и боковой поверхности.
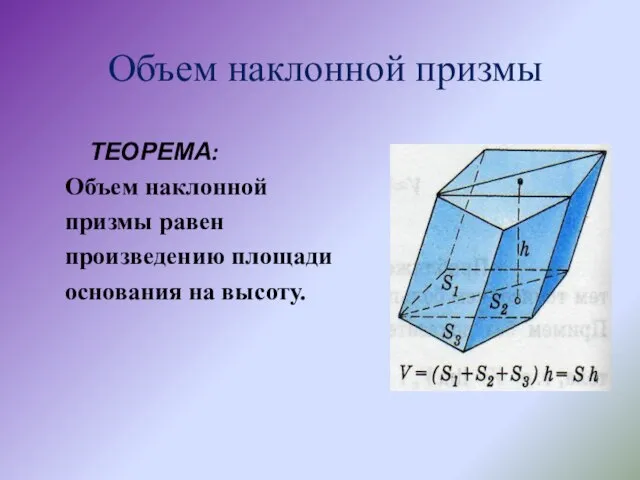
Высотой призмы называется отрезок, являющийся общим перпендикуляром плоскостей, в которых лежат основания призмы.
Высота призмы равна расстоянию h между плоскостями оснований.










 Цветовые созвучия
Цветовые созвучия Как начать зарабатывать на профессии криптоконсультант
Как начать зарабатывать на профессии криптоконсультант Проект Ecowiki.ru Комьюнити-проект в концепции веб 2.0 Старт проекта – январь 2009 Вики-платформа и вики-подход. Викификация. - презентация
Проект Ecowiki.ru Комьюнити-проект в концепции веб 2.0 Старт проекта – январь 2009 Вики-платформа и вики-подход. Викификация. - презентация Журнал «Энергетика и коммунальное хозяйство Республики Казахстан»
Журнал «Энергетика и коммунальное хозяйство Республики Казахстан» Март 2008 Лидирующие позиции по охвату слушателей в Москве и Санкт-Петербурге ОХВАТ Реформатирование частоты в мае 2003 г. - стремитель
Март 2008 Лидирующие позиции по охвату слушателей в Москве и Санкт-Петербурге ОХВАТ Реформатирование частоты в мае 2003 г. - стремитель Тема урока: «Географическое положение Австралии»
Тема урока: «Географическое положение Австралии» Завершили рыбацкий сезон 2015 года
Завершили рыбацкий сезон 2015 года Налоги и налоговая система
Налоги и налоговая система Презентация на тему ЖОСТОВО РОСПИСЬ ПО МЕТАЛЛУ
Презентация на тему ЖОСТОВО РОСПИСЬ ПО МЕТАЛЛУ  ПРЕЗЕНТАЦИЯ ДОРОЖНОЙ КАРТЫСпособы и методы организации образовательной деятельности, обеспечивающие формирование общих и про
ПРЕЗЕНТАЦИЯ ДОРОЖНОЙ КАРТЫСпособы и методы организации образовательной деятельности, обеспечивающие формирование общих и про Информационная компетенция
Информационная компетенция С Днём города!
С Днём города! Социальная поддержка и социальное обслуживание граждан пожилого возраста (Направление на социальное обслуживание в государствен
Социальная поддержка и социальное обслуживание граждан пожилого возраста (Направление на социальное обслуживание в государствен Макет кабинета психогаконсультанта
Макет кабинета психогаконсультанта Универсальные кухонные приводы
Универсальные кухонные приводы Дополнительные материалы
Дополнительные материалы Спортивно-оздоровительныйкомплекс БГУ «Бригантина» 15-17 февраля 2008 г.
Спортивно-оздоровительныйкомплекс БГУ «Бригантина» 15-17 февраля 2008 г. Обмерные работы для целей реконструкции и реставрации сооружений. Лекция тема 7
Обмерные работы для целей реконструкции и реставрации сооружений. Лекция тема 7 Счёт предметов (1 класс)
Счёт предметов (1 класс) Мордовский национальный костюм
Мордовский национальный костюм Презентация на тему Гегель: абсолютный идеализм
Презентация на тему Гегель: абсолютный идеализм  Образы животных в английских сказках. Межрегиональная дистанционная конференция – конкурс учащихся 1 – 7 классов «Первые шаги в н
Образы животных в английских сказках. Межрегиональная дистанционная конференция – конкурс учащихся 1 – 7 классов «Первые шаги в н Изменения в Законе о контрактной системе № 44-ФЗ
Изменения в Законе о контрактной системе № 44-ФЗ Производственный распорядок дня
Производственный распорядок дня Класс земноводные. Особенности строения и жизнедеятельности как примитивных сухопутных животных
Класс земноводные. Особенности строения и жизнедеятельности как примитивных сухопутных животных Учёт расчётов с разными дебиторами и кредиторами. Счет 76
Учёт расчётов с разными дебиторами и кредиторами. Счет 76 Киберспортивный клуб GameHak
Киберспортивный клуб GameHak Художественный язык и жанры графики
Художественный язык и жанры графики