Признаки параллельных прямых

Цели:
Закрепить знания учащимися видов углов,
образованных в результате пересечения двух прямых
секущей; изучить признаки параллельности прямых;
формирование умений анализировать изученный материал
и навыков применения его для решения задач; показать
значимость изучаемых понятий; закрепить навыков
решения задач на применение признаков параллельности
прямых;
развитие познавательной активности и самостоятельности
получения знаний;
воспитание интереса к предмету, самостоятельности.

Две прямые параллельны, если они не пересекаются.
а
b

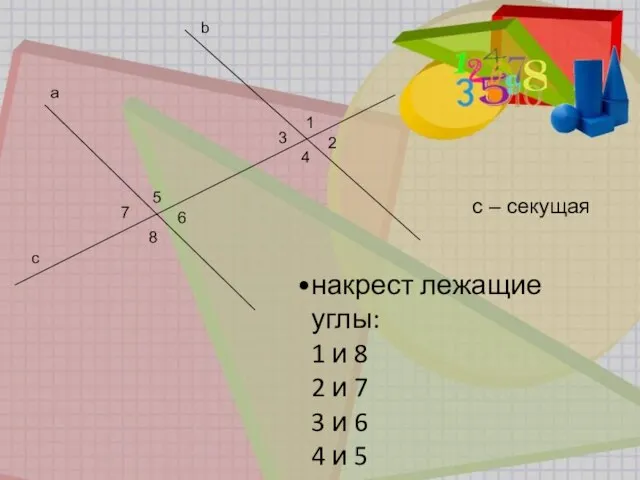
b
a
1
2
3
4
5
6
7
8
c
с – секущая
накрест лежащие углы:
1 и 8
2 и 7
3 и 6
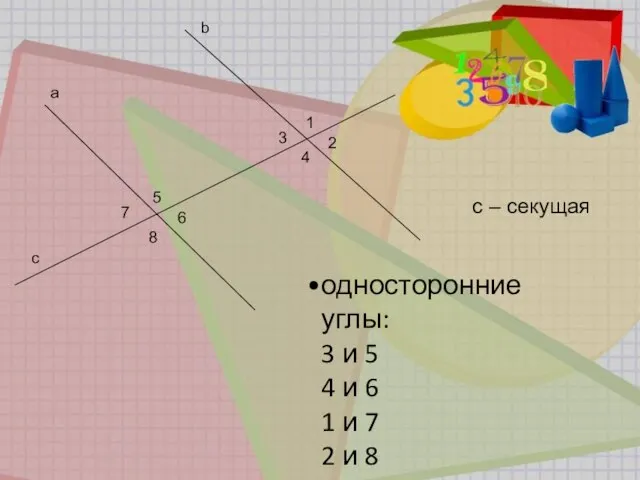
4 и 5

b
a
1
2
3
4
5
6
7
8
c
с – секущая
односторонние углы:
3 и 5
4 и 6
1 и 7
2 и 8

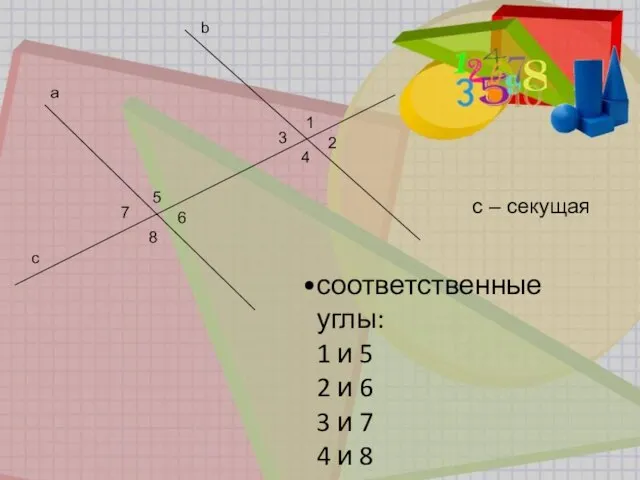
b
a
1
2
3
4
5
6
7
8
c
с – секущая
соответственные углы:
1 и 5
2 и 6
3 и 7
4 и 8

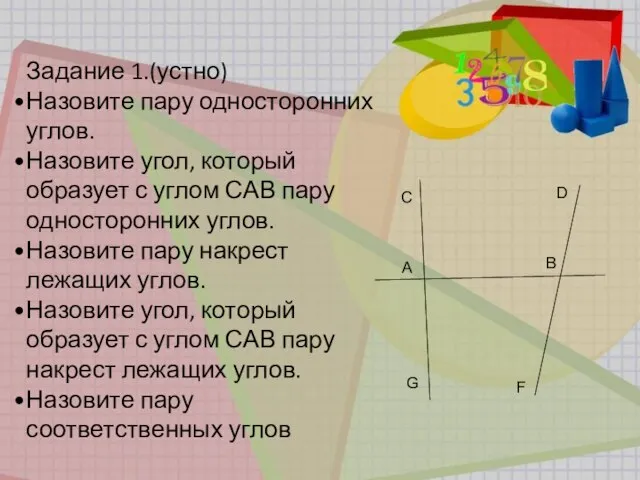
Задание 1.(устно)
Назовите пару односторонних углов.
Назовите угол, который образует с углом САВ пару односторонних углов.
Назовите пару накрест лежащих углов.
Назовите угол, который образует с углом САВ пару накрест лежащих углов.
Назовите пару соответственных углов
C
A
G
D
B
F

Признак 1.
Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
Дано: а и b – прямые с - секущая 1 = 2
Доказать: а||b
a
b
c
A
B
1
2

Доказательство :
Случай 1.
Угол 1 и 2 по 90°.По теореме о двух прямых, перпендикулярных третьей, а ||‖ b
а
b
c
A
B
1
2

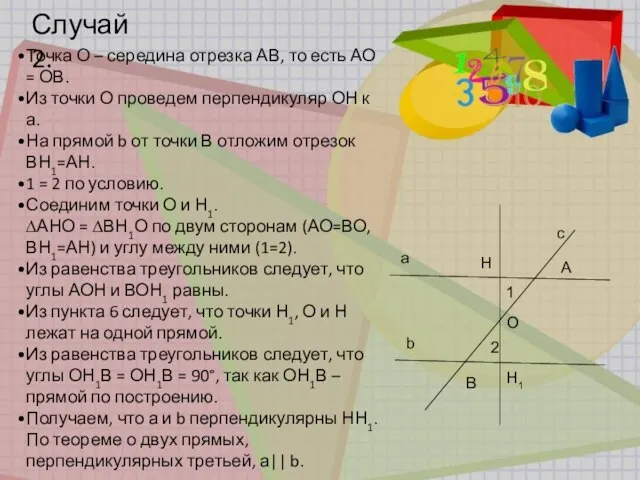
Случай 2.
a
b
c
A
B
1
2
H
H1
O
Точка О – середина отрезка АВ, то есть АО = ОВ.
Из точки О проведем перпендикуляр ОН к а.
На прямой b от точки В отложим отрезок ВН1=АН.
1 = 2 по условию.
Соединим точки О и Н1.
∆АНО = ∆ВН1О по двум сторонам (АО=ВО, ВН1=АН) и углу между ними (1=2).
Из равенства треугольников следует, что углы АОН и ВОН1 равны.
Из пункта 6 следует, что точки Н1, О и Н лежат на одной прямой.
Из равенства треугольников следует, что углы ОН1В = ОН1В = 90°, так как ОН1В – прямой по построению.
Получаем, что а и b перпендикулярны НН1. По теореме о двух прямых, перпендикулярных третьей, а|| b.

Признак 2.
Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны.
Признак 3.
Если при пересечении прямых секущей соответственные углы равны, то прямые параллельны.
(доказательства самостоятельно дома)

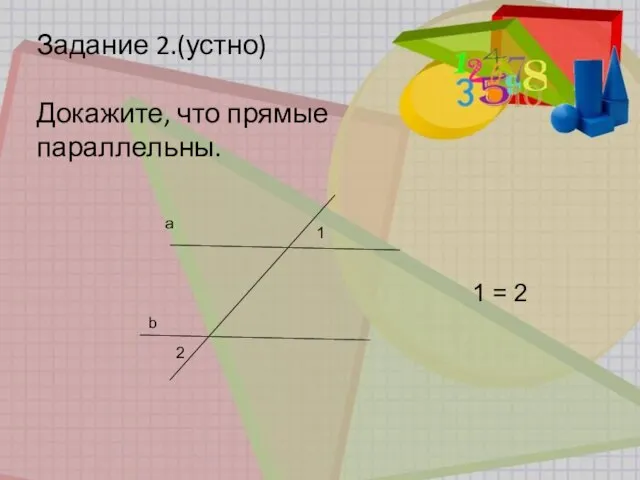
Задание 2.(устно)
Докажите, что прямые параллельны.
1 = 2
a
b
2
1

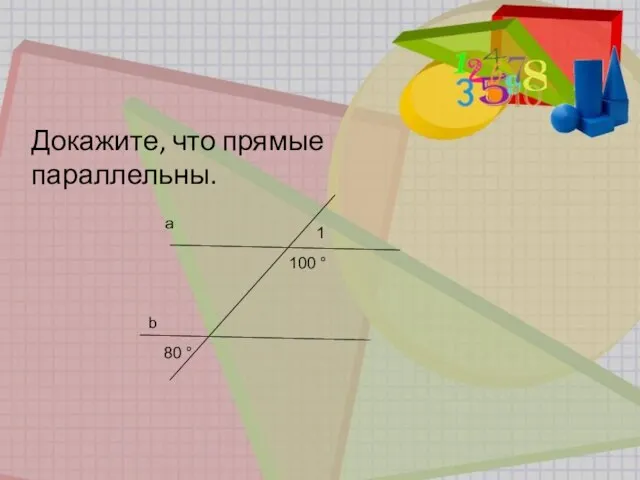
a
b
80 °
1
100 °
Докажите, что прямые параллельны.