Слайд 2Recap
Why should we learn Probability?
Formulating questions in terms of probability
Building the

probability model
Four-step Method
Uniform sample spaces
Counting
Слайд 3Today’s Objectives
Counting subsets of a set
Conditional Probability
Independence
Total Probability Theorem
Baye’s theorem
Random variables

Слайд 5Why Count Subsets of Set?
Example:
Suppose we select 5 cards at random

from a deck of 52 cards.
What is the probability that we will end up having a full house?
Doing this using the possibility tree will take some effort.
Слайд 14Conditional Probability
An Interesting Kind of Probability Question
“After this lecture, when I

go to UI canteen for lunch, what is the probability that today they will be serving biryani (my favorite food)?
Слайд 16Conditional Probability
Of course, the vast majority of the food that the

cafeteria prepares is NEITHER delicious NOR is it ever biryani (low probability).
But they do cook dishes that contain rice, so now the question is “what’s the probability that food from UI is delicious given that it contains rice?”
This is called “Conditional Probability”
Слайд 17Conditional Probability
What is the probability that it will rain this afternoon,

given that it is cloudy this morning?
What is the probability that two rolled dice sum to 10, given that both are odd?
Written as
P(A|B) – denotes the probability of event A, given that event B happens.
Слайд 18Conditional Probability
So, how to answer the “Food Court” question?

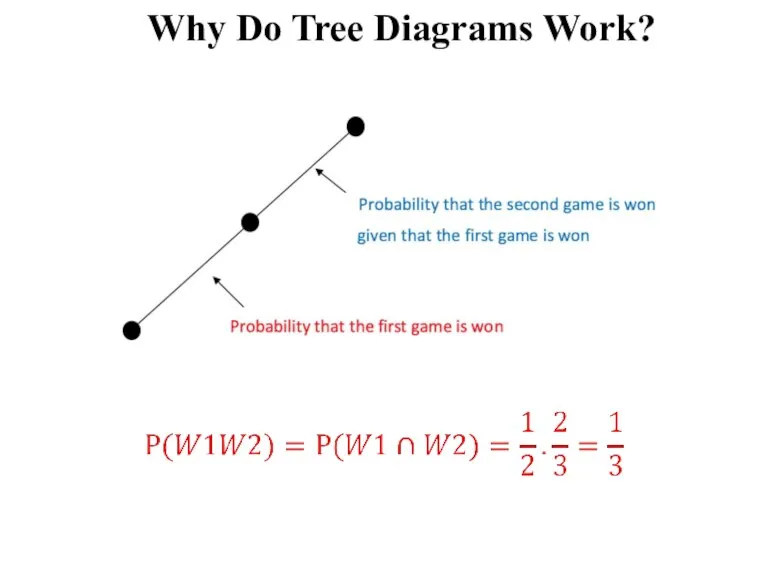
Слайд 20Why Do Tree Diagrams Work?
We have solved multiple probability problems using tree

diagrams
Let’s think for a moment about “why do tree diagrams work?”
The answer involves conditional probabilities
In fact, the probabilities that we have been recording on the edges of a tree diagram are conditional probabilities
More generally, on each edge of a tree diagram, we record that the probability that the experiment proceeds along that part, given that it reaches the parent vertex
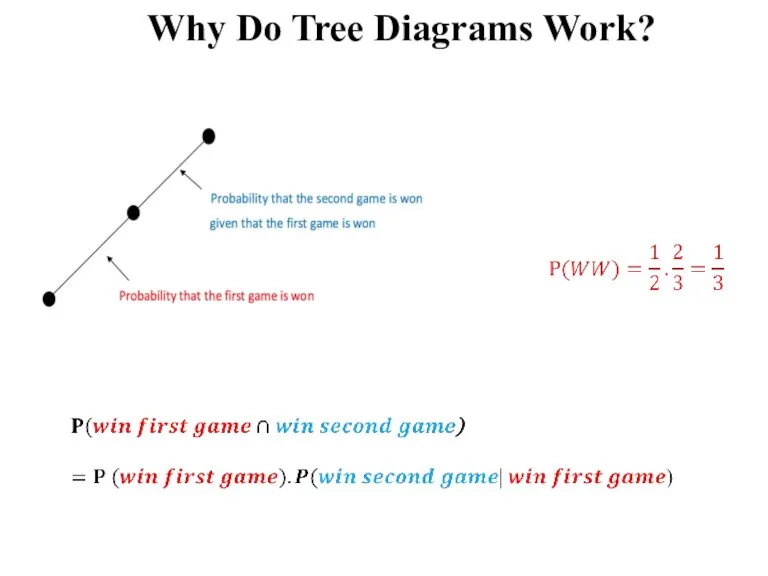
Слайд 21Why Do Tree Diagrams Work?
Let’s look the upper most edges of the
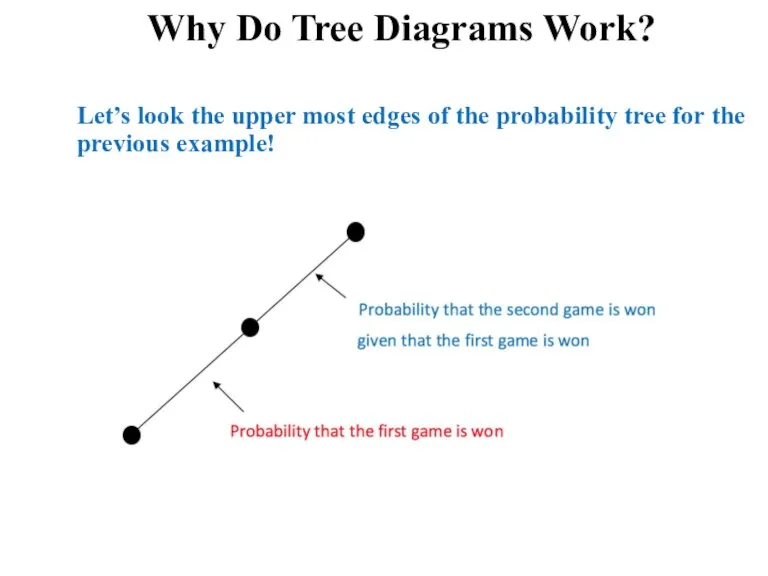
probability tree for the previous example!
Слайд 24Why Do Tree Diagrams Work?
“So the Product Rule is the formal justification

for multiplying edge probabilities in a probability tree to get outcome probabilities”
Слайд 31What Independence Really Means?
Are these events independent?
A
B

Слайд 32What Independence Really Means?
Thus being dependent is completely different from being disjoint!

Слайд 33What Independence Really Means?
Thus being dependent is completely different from being disjoint!
Two

events are independent, if the occurrence of one does not change our belief about the occurrence of the other.
Слайд 34What Independence Really Means?
Thus being dependent is completely different from being disjoint!
Two

events are independent, if the occurrence of one does not change our belief about the occurrence of the other.
Typically the case when the two events are determined by two physically distinct and non-interacting processes.
Getting heads in a coin toss and snowing outside
Слайд 35Independence---Cont.
Generally, independence is an assumption that we assume when modeling a

phenomenon.
The reason we so-often assume statistical independence is not because of its real-world accuracy
It is because of its armchair appeal: It makes the math easy
How does it do that?
By splitting a compound probability into a product of individual probabilities.
(Note for TAs: Include example of Independence assumption in tutorials)
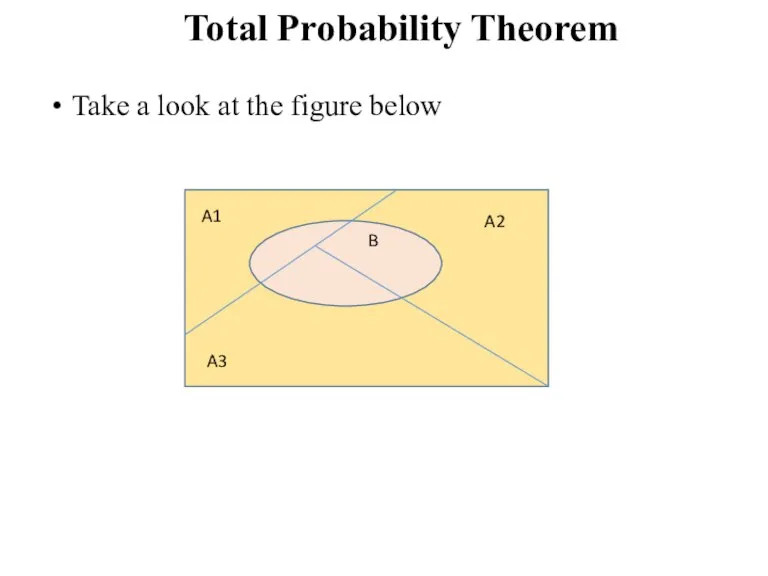
Слайд 36Total Probability Theorem
Take a look at the figure below
A1
A2
A3
B
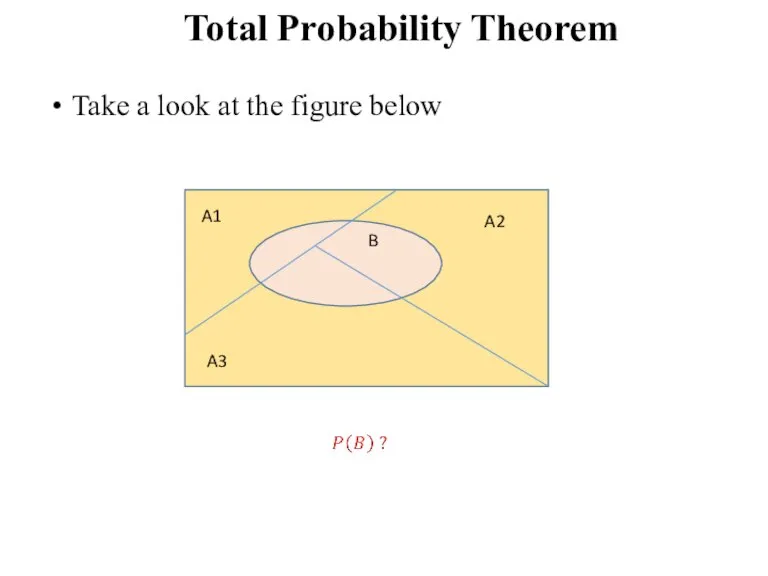
Слайд 37Total Probability Theorem
Take a look at the figure below
A1
A2
A3
B
Слайд 38Total Probability Theorem
Take a look at the figure below
A1
A2
A3
B

Слайд 39Total Probability Theorem
Take a look at the figure below
A1
A2
A3
B

Слайд 40Total Probability Theorem
Take a look at the figure below
A1
A2
A3
B

Слайд 41Total Probability Theorem
Where do we use it?
Baye’s Theorem!

Слайд 42Medical Testing Problem
Let’s assume a “not-so-perfect” test for a medical condition called

BO suffered by 10% of the population
The test is not-so-perfect because
90% of the tests come positive if you have BO
70% of the tests come negative if you don’t have BO
If we randomly test a person for BO, and if the test comes positive, what is the probability that the person has BO.
Слайд 43Probability Tree
A: The test came positive
B: The person has BO
BO is

suffered by 10% of the population
If someone has BO, there is a 90% chance that the test will be positive
If someone does not have the condition, there is a 70% chance that the test will be negative.
Слайд 45Conditional Probability Tree---Cont.
Surprising, Right!
So if the test comes out positive, the

person has only 25% chance of having the diseases
Conclusion:
Tests are flawed
Tests give test probabilities not the real probabilities
Слайд 48Bayes Theorem---Cont.
A Posteriori Probabilities
For example:
The probability that it was cloudy

this morning, given that it rained in the afternoon.
Mathematically speaking, there is no difference between a posteriori probability and a conditional probability.
Слайд 54Random Variables
So far, we focused on probabilities of events.
For example,
The

probability that someone wins the Monty Hall Game
The probability that someone has a rare medical condition given that he/she tests positive
Слайд 55Random Variables
But most often, we are interested in knowing more than

this.
For example,
How many players must play Monty Hall Game before one of them finally wins?
How long will a weather certain condition last?
How long will I loose gambling with a strange coin all night?
To be able to answer such questions, we have to learn about “Random Variables”
Слайд 56Random Variables---Cont.
“Random Variables” are nothing but “functions”
A random variable R on a

probability space is a function whose domain is the sample space and whose range is a set of Real numbers.
Слайд 57Random Variables---Cont.
“Random Variables” are nothing but “functions”
A random variable R on a

probability space is a function whose domain is the sample space and whose range is a set of Real numbers.
Let’s look at this example!
Tossing three independent coins and noting
C: the number of heads that appear
M: 1 if all are heads or tails, 0 otherwise
If we look closely, we will see that C and M are in fact functions that map every outcome of the experiment to a number.
Слайд 63Expected Value
Weighted average of the values of a random variable
Provides a central

point for the distribution of the values of a random variable
We can solve many problems using the notion of expected values
How many heads are expected to appear if a coin is tossed 100 times?
What is the expected number of comparisons used to find an element in a list using the linear search?
Слайд 66Variance
Consider the following two gambling games:
Game A: You win $2 with

probability 2/3 and lose $1 with probability 1/3.
Game B: You win $1002 with probability 2=3 and lose $2001 with probabil- ity 1=3.
Which game would you play?
Слайд 67Variance
Let’s compute the expected return for both games:

Слайд 71Variance
Game A: You win $2 with probability 2/3 and lose $1

with probability 1/3.
Слайд 72Variance
For game B
Intuitively, this means that the payoff in Game A

is usually close to the expected value of $1, but the payoff in Game B can deviate very far from this expected value – high variance means high risk.
Слайд 73Standard Deviation
Because of its definition in terms of the square of

a random variable, the variance of a random variable may be very far from a typical deviation from the mean.
Слайд 74Standard Deviation
For example, in Game B above, the deviation from the

mean is 1001 in one outcome and -2002 in the other. But the variance is a whopping 2,004,002
The problem is with the “units” of variance.
If a random variable is in dollars, then the expected value is also in dollars, but the variance is in square dollars




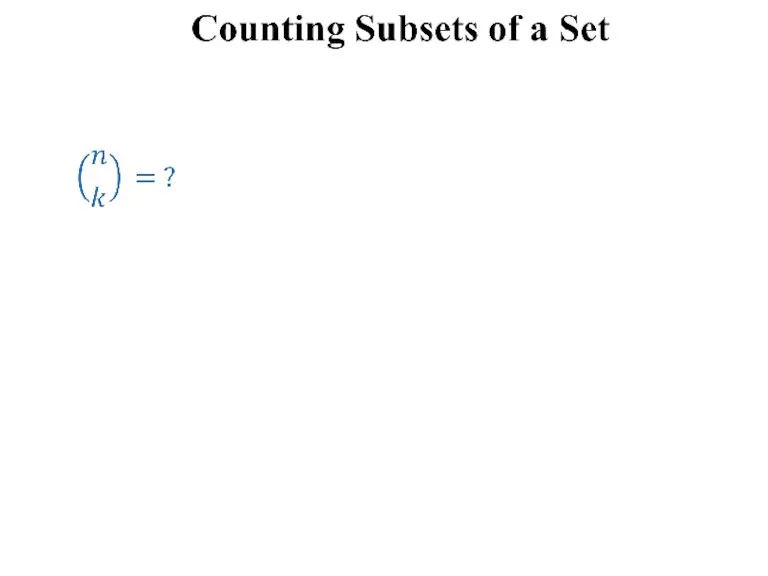


































































 Школа Сомелье. Винотека
Школа Сомелье. Винотека Художественная гладь
Художественная гладь Занятие 1 презентация
Занятие 1 презентация Спортивные комплексы
Спортивные комплексы Презентация на тему Автомобили - старинные и современные
Презентация на тему Автомобили - старинные и современные Основания стеблей морских лилий
Основания стеблей морских лилий М.Ю. Лермонтов. Рассказ о поэте. Историческая основа стихотворения "Бородино"
М.Ю. Лермонтов. Рассказ о поэте. Историческая основа стихотворения "Бородино" Презентация на тему Число и цифра 4
Презентация на тему Число и цифра 4 Тема учебного проекта: «Безопасность детей на дороге»
Тема учебного проекта: «Безопасность детей на дороге» Полезные ископаемые Кемеровской области
Полезные ископаемые Кемеровской области Однородные члены предложения. Знаки препинания между однородными членами предложения
Однородные члены предложения. Знаки препинания между однородными членами предложения Почему электрошпиндель и мотор-шпиндель имеют различные области применения?
Почему электрошпиндель и мотор-шпиндель имеют различные области применения? Литейное производство. Опоки. (Лекция 5)
Литейное производство. Опоки. (Лекция 5) Презентация на тему Национальные особенности русской философии
Презентация на тему Национальные особенности русской философии Великие математики
Великие математики Презентация участников команды №1 Бухгалтерский дозор
Презентация участников команды №1 Бухгалтерский дозор ALT Linux HPC
ALT Linux HPC Качество и надежность HDTV-вещания в различных средах
Качество и надежность HDTV-вещания в различных средах Компанию Наш продукт плюс
Компанию Наш продукт плюс Сино-тибетская семья
Сино-тибетская семья Социальная среда подростка (7 класс)
Социальная среда подростка (7 класс) Современные подходы к мотивации персонала в организации
Современные подходы к мотивации персонала в организации Н е д е л я д е т с к о й к н и г и 2011 – 2012 учебный год
Н е д е л я д е т с к о й к н и г и 2011 – 2012 учебный год Каролингское возрождение
Каролингское возрождение Презентация на тему антарктида 7 класс
Презентация на тему антарктида 7 класс ВРЕМЕНА ГОДА SEASONS
ВРЕМЕНА ГОДА SEASONS  Дециметр
Дециметр История. Портреты
История. Портреты