Содержание
- 2. Актуальность:Актуальность данной темы заключается в том,что имитационное моделирование на цифровых вычислительных машинах является одним из наиболее
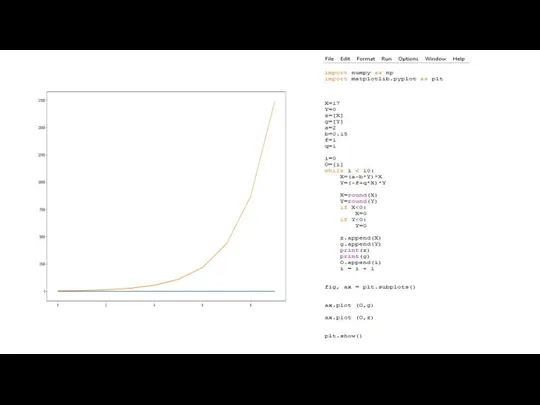
- 3. Цель:найти оптимальный способ визуализации имитационных моделей, на примере системы “хищник-жертва” Задачи : построить систему хищник-жертва визуализировать
- 4. Ход работы В качестве имитационной модели для последующей ее визуализации мной была выбрана модель хищник-жертва. Система
- 6. x — численность жертв (травоядных); y — численность хищников; α — вероятность того, что травоядные размножатся;
- 9. Скачать презентацию
Слайд 2Актуальность:Актуальность данной темы заключается в том,что имитационное моделирование на цифровых вычислительных машинах
Актуальность:Актуальность данной темы заключается в том,что имитационное моделирование на цифровых вычислительных машинах

является одним из наиболее мощных средств исследования, в частности сложных динамических систем.Имитационные системы используют практически во всех сферах жизни(бизнес процессах,производстве,логике).имитационное моделирование-Метод исследования, при котором изучаемая система заменяется моделью, с достаточной точностью описывающей реальную систему, с которой проводятся эксперименты с целью получения информации об этой системе.
Проблемой проекта является выбор имитационной модели для ее визуализации.
Гипотеза:Существует универсальный способ визуализации имитационных моделей.
Учебный предмет: информатика
Близкие к теме: биология и математика
Тип проекта: теоретический
объект исследования : модель хищник-жертва
Проблемой проекта является выбор имитационной модели для ее визуализации.
Гипотеза:Существует универсальный способ визуализации имитационных моделей.
Учебный предмет: информатика
Близкие к теме: биология и математика
Тип проекта: теоретический
объект исследования : модель хищник-жертва
Слайд 3Цель:найти оптимальный способ визуализации имитационных моделей, на примере системы “хищник-жертва”
Задачи :
построить
Цель:найти оптимальный способ визуализации имитационных моделей, на примере системы “хищник-жертва”
Задачи :
построить

систему хищник-жертва
визуализировать ее несколькими способами
выбрать оптимальный способ
найти практическое применение полученному опыту визуализации.
Методы исследования:моделирование,анализ,сравнение,
визуализация.
Практическая ценность:благодаря систематизации данных будет выбран оптимальный способ, визуализации который можно будет использовать во многих сферах.
визуализировать ее несколькими способами
выбрать оптимальный способ
найти практическое применение полученному опыту визуализации.
Методы исследования:моделирование,анализ,сравнение,
визуализация.
Практическая ценность:благодаря систематизации данных будет выбран оптимальный способ, визуализации который можно будет использовать во многих сферах.
Слайд 4Ход работы
В качестве имитационной модели для последующей ее визуализации мной была выбрана
Ход работы
В качестве имитационной модели для последующей ее визуализации мной была выбрана

модель хищник-жертва.
Система «хищник — жертва» — сложная экосистема, для которой реализованы долговременные отношения между видами хищника и жертвы, типичный пример коэволюция( совместная эволюцияя биологических видов).Для реализации имитационной модели мной использована Моде́ль Ло́тки — Вольте́рры — модель взаимодействия двух видов типа «хищник — жертва», названная в честь её авторов (Альфреда Джеймса Лотка и Вито Вольтерра), которые предложили модельные уравнения независимо друг от друга в 1925 и 1926 соответственно.
Такие уравнения можно использовать для моделирования систем «хищник — жертва», «паразит — хозяин», конкуренции и других видов взаимодействия между двумя видами.
В математической форме предложенная система имеет следующий вид:
Система «хищник — жертва» — сложная экосистема, для которой реализованы долговременные отношения между видами хищника и жертвы, типичный пример коэволюция( совместная эволюцияя биологических видов).Для реализации имитационной модели мной использована Моде́ль Ло́тки — Вольте́рры — модель взаимодействия двух видов типа «хищник — жертва», названная в честь её авторов (Альфреда Джеймса Лотка и Вито Вольтерра), которые предложили модельные уравнения независимо друг от друга в 1925 и 1926 соответственно.
Такие уравнения можно использовать для моделирования систем «хищник — жертва», «паразит — хозяин», конкуренции и других видов взаимодействия между двумя видами.
В математической форме предложенная система имеет следующий вид:
Слайд 6x — численность жертв (травоядных);
y — численность хищников;
α — вероятность того, что
x — численность жертв (травоядных);
y — численность хищников;
α — вероятность того, что

травоядные размножатся;
β — вероятность того, что травоядное будет съедено хищником;
γ — вероятность того, что хищник умрет от голода;
δ — вероятность того, что хищнику хватит еды на дальнейшее размножение.
Стоит отметить, что в данной модели принимаются несколько допущений:
Количество пищи для травоядных не ограничено;
Ни жертвы, ни хищники не эмигрируют из среды;
Никакие другие животные не мигрируют в среду;
Данная модель не учитывает вымирание животных по причине старения и прочих внешних воздействий.
β — вероятность того, что травоядное будет съедено хищником;
γ — вероятность того, что хищник умрет от голода;
δ — вероятность того, что хищнику хватит еды на дальнейшее размножение.
Стоит отметить, что в данной модели принимаются несколько допущений:
Количество пищи для травоядных не ограничено;
Ни жертвы, ни хищники не эмигрируют из среды;
Никакие другие животные не мигрируют в среду;
Данная модель не учитывает вымирание животных по причине старения и прочих внешних воздействий.
- Предыдущая
Учение о двойственной истине Ибн-РушдаСледующая -
konkurenty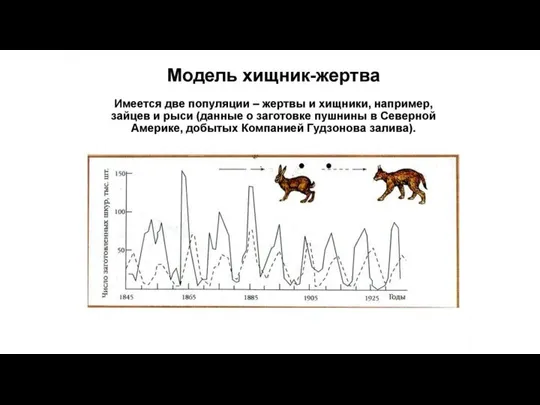
 История становления политических партий 19-20 вв
История становления политических партий 19-20 вв Хран бонус (1)
Хран бонус (1) Тёплый дом
Тёплый дом ст.157, 264.4 БК РФ
ст.157, 264.4 БК РФ Кружок « Пресс-центр»
Кружок « Пресс-центр» Портфолио педагога - психолога Вильховой Ксении Леонидовны
Портфолио педагога - психолога Вильховой Ксении Леонидовны 俄罗斯叶卡 捷琳堡设计方案 - Philippines design program
俄罗斯叶卡 捷琳堡设计方案 - Philippines design program Чикаго
Чикаго Абсолютная защита вашей кожи. ADPCosmetics
Абсолютная защита вашей кожи. ADPCosmetics Исторические личности
Исторические личности МЕНЕДЖМЕНТ
МЕНЕДЖМЕНТ День студента
День студента Question tags Разделительные вопросы
Question tags Разделительные вопросы презентация под проект
презентация под проект НП «Институт социально-экономического развития Центрального федерального округа»
НП «Институт социально-экономического развития Центрального федерального округа» МЫ ЗА ЗДОРОВЫЙ ОБРАЗ ЖИЗНИ!
МЫ ЗА ЗДОРОВЫЙ ОБРАЗ ЖИЗНИ! Презентация проекта «Химия и литература»
Презентация проекта «Химия и литература» Промышленные стали
Промышленные стали Военная служба по контракту в вооруженных силах Российской Федерации
Военная служба по контракту в вооруженных силах Российской Федерации «Поощрение и наказание в воспитании детей.»
«Поощрение и наказание в воспитании детей.» Цель Отработать навыки: формирования запросов с использованием логических операций; создания вычисляемых полей.
Цель Отработать навыки: формирования запросов с использованием логических операций; создания вычисляемых полей. Эмоциональный интеллект . Актуальный профиль компетенций специалиста XXI века
Эмоциональный интеллект . Актуальный профиль компетенций специалиста XXI века Осеннее дерево (штампография)
Осеннее дерево (штампография) Салат-бар
Салат-бар Адаптация спортсменов к выполнению специфических статических нагрузок
Адаптация спортсменов к выполнению специфических статических нагрузок Родильная обрядность сынских хантов
Родильная обрядность сынских хантов ВОЛОГОДСКИЙ ОБЛАСТНОЙ ИНФОРМАЦИОННО-АНАЛИТИЧЕСКИЙ ЦЕНТР КУЛЬТУРЫ
ВОЛОГОДСКИЙ ОБЛАСТНОЙ ИНФОРМАЦИОННО-АНАЛИТИЧЕСКИЙ ЦЕНТР КУЛЬТУРЫ Шакирова Олеся ученица 9 класса Гурульбинская СОШ
Шакирова Олеся ученица 9 класса Гурульбинская СОШ