Проценты в финансовой отросли.Кредиты

Содержание
Вступление. Математика в финансовой отросли.
Проценты
Простые проценты.
Переменная ставка
Возврат кредита по частям
- актуарный метод
- метод торговца
с) Дисконтирование (учет)
d) Номинальная и реальная ставки процента
e) Конверсия валюты
4. Сложные проценты

Финансовая математика
Базовая финансовая операция – кредитование.
Субъекты рынка заключают сделку: кредитор выдает деньги заемщику с условием, в отведенный срок тот вернет кредит с процентами.
Обратите внимание: процентом называют величину наращивания ссуды и измеряется в денежном эквиваленте, а не в процентах.
Рассмотрит простейший случай кредитования с ссудой выданной на год:
Р- размер кредита
S- кредит с наращением(с процентами);
I-процент;
I=S-P
і=I/P=(S-P)/P→S=P(1+і)

Возврат кредита по частям.
Актуарный метод
Обозначения:
Р – кредит
t=1,…,m –номера платежей
nt – срок t-ого платежа
І – годовая ставка
St - сумма долга к t-ому платежу
Rt – величина t-ого платежа
Рt – остаток долга после t-го платежа.
St = Pt-1(1 + ( nt – nt-1) i );
P­t = St - Rt.
Розмер последнего платежа:
Rm = Sm = Pm-1 ( 1 + (n – nm-1) i).

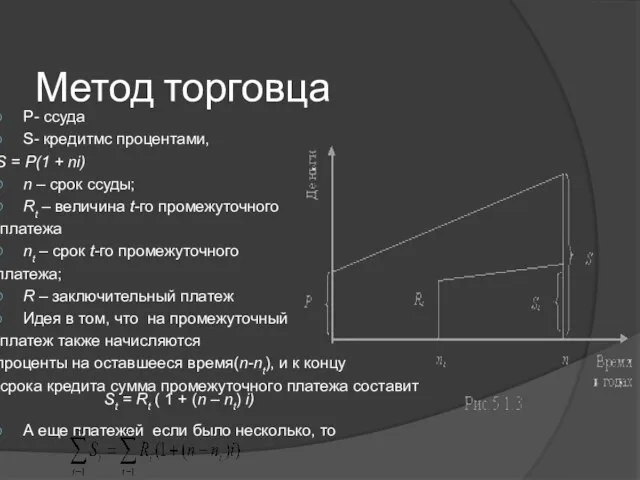
Метод торговца
Р- ссуда
S- кредитмс процентами,
S = P(1 + ni)
n – срок ссуды;
Rt – величина t-го промежуточного
платежа
nt ­– срок t-го промежуточного
платежа;
R – заключительный платеж
Идея в том, что на промежуточный
платеж также начисляются
проценты на оставшееся время(n-nt), и к концу
срока кредита сумма промежуточного платежа составит
А еще платежей если было несколько, то
St = Rt ( 1 + (n – nt) i)

Дисконтирование
Обозначим:
S – номинал векселя;
1 год – срок действия векселя;
D – дисконт, т.е. скидка с номинала при учете векселя;
Р – цена векселя, т.е. сумма денег, которую получит продавец векселя при его учете.
D = S-P или P = S-D. →
d – учетная ставка,
d =
При известных S и d запишем формулу расчета для P:
P = S(1- d), и для срока меньше года
P = S(1-nd), где 1 > nd > 0.

Номинальная и реальная ставки процента
Обозначим:
Sн – номинальная ссуда с процентами;
Sр – реальная ссуда с процентами, т.е. покупательная способность Sн;
r – реальная ставка процента;
i – номинальная ставка процента;
j – темп инфляции.
С учетом принятых обозначений, формулы наращения примут вид:
Sн = P(1 + i);
SP = P(1 + r);
Sн = SP (1 + j) = P(1 + r)(1 + j).
Вместо Sн подставим ее значение:
P(1 + i) = P(1 + r) (1+ j) или (1 + i) = (1 + r)(1 + j)
отсюда

конверсия
Стрелка АВ – хранение денег на рублевом вкладе.
АС – конверсия рублей в доллары, т.е. продажа банком долларов вкладчику.
CD – хранение денег на валютном вкладе.
DB – конверсия долларов в рубли.
РP– сумма вклада в рублях.
Р – сумма вклада в долларах.
SP – рублевая сумма вклада с наращением (с процентами) через год.
S – долларовый вклад с процентами через год.
i – годовая ставка процента по рублевому вкладу.
v – годовая ставка процента по валютному вкладу.
bпр – курс продажи на момент вклада, т.е. цена по которой банк продает доллары за рубли.
bпок – курс покупки через год, т.е. цена , по которой банк покупает доллары.

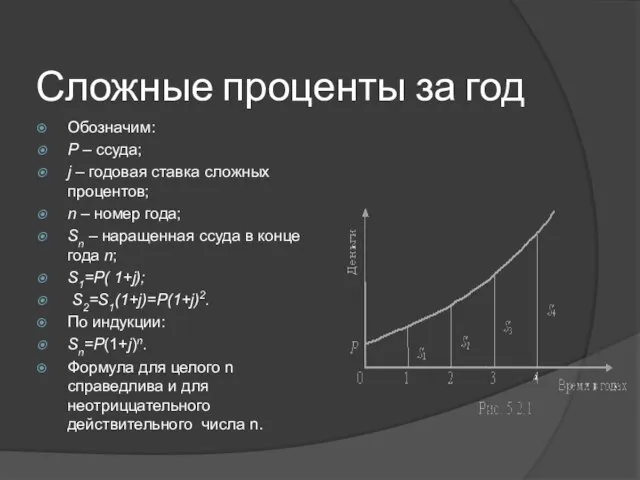
Сложные проценты за год
Обозначим:
Р – ссуда;
j – годовая ставка сложных процентов;
n – номер года;
Sn – наращенная ссуда в конце года n;
S1=P( 1+j);
S2=S1(1+j)=P(1+j)2­­­­­­­.
По индукции:
Sn=P(1+j)n­.
Формула для целого n справедлива и для неотриццательного действительного числа n.

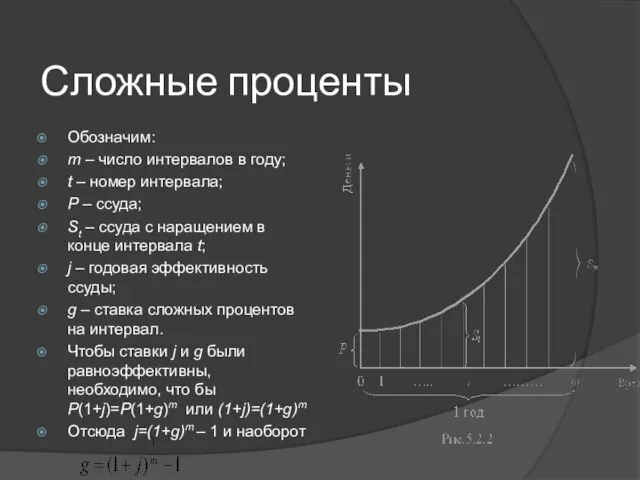
Сложные проценты
Обозначим:
m – число интервалов в году;
t – номер интервала;
Р – ссуда;
St – ссуда с наращением в конце интервала t;
j – годовая эффективность ссуды;
g – ставка сложных процентов на интервал.
Чтобы ставки j и g были равноэффективны, необходимо, что бы P(1+j)=P(1+g)m или (1+j)=(1+g)m
Отсюда j=(1+g)m – 1 и наоборот