Проект:« Модуль числа»

Цель проекта:
Формирование понятия модуля и умения выполнять действия с ними.

Задачи проекта:
Определить значимость темы «Модуль» в математике.
Углубить теоретические знания по решению упражнений с модулем;
Оформление пособия исследовательской деятельности при решении задач с модулями;
Составить пособие нестандартных задач с модулями.

Этапы работы над проектом:
1-й погружение в проект;
2-й организация деятельности;
3-й выпуск пособия «Решение упражнений с модулем »;
4-й презентация результатов

Паспорт учебного проекта:
Тема: «Модуль числа»
Предмет: математика
Класс: 7 - 8
Тип проекта: монопредметный, практико - ориентированный
Форма работы: внеурочная

Цели:
1. Развивать умение исследовать, проектировать в процессе анализа решения уравнения или неравенства с модулем;
Развивать умение работать с информационными технологиями.
2. Выпустить пособие для школьников.

Мотивация:
Основывается на интересе учащихся к данной теме, и их желании получить знания по теме «Модуль», умений решать уравнения и неравенства с модулем.
Подготовка к ГИА.

Ход стратегических действий:
1 – подбор литературы ,введение, определении значимости модуля; 2– способы решения уравнений и неравенств с модулем, выпуск пособия;
3 – оформление материала, презетация.

Информационно-техническое обеспечение.
1. При работе с проектом использовался компьютер, дополнительная литература, услуги Интернета, подготовлены схемы решения уравнений и неравенств ;
2. Решение уравнения:
а) график функции;
б) умения работать с дополнительной литературой;
в) умения проводить аналогию.

Предполагаемые результаты:
Развитие:
- самостоятельной работы с источниками информации;
- умения решать упражнения с модулем
- самостоятельности в принятии решений
- коммуникативности;
- проектирования, планирования, анализа.

Введение.
Главной целью этого проекта является расширение и углубление знаний, развитие интереса к предмету, развитие математических способностей.

Значение проекта:
Большую роль в развитии математического мышления играет изучение темы «Модуль числа».
Вместе с тем изучению этой темы в школьной программе не уделено достаточно внимания, в 6 и 7 классах изучаются самые азы понятия модуля и действия с ними.
Интерес к теме объясняется тем, что уравнения с модулем предлагаются на школьных экзаменах (на ГИА и ЕГЭ).

Что такое модуль?
Слово «модуль» произошло от латинского слова «modulus», что в переводе означает «мера».
Это многозначное слово , которое имеет множество значений и применяется не только в математике, но и в физике, технике, программировании и других точных науках.
В технике – это термин служит для обозначения различных коэффициентов и величин, например модуль зацепления, модуль упругости.
В физике - это модуль объемного сжатия, отношение нормального напряжения в материале к относительному удлинению.

Понятия и определения.
Уравнение – это равенство, содержащее переменные.
Уравнение с модулем – это уравнение, содержащее переменную под знаком абсолютной величины (под знаком модуля). Например: | х | = 1
Решить уравнение – это значит найти все его корни, или доказать, что корней нет.
Модуль – расстояние от начала отсчета до точки на числовой прямой.

Определение модуля числа.
Модуль – это расстояние от начала отсчета до точки на числовой прямой.
А это значит:
Модуль числа а равен а, если а больше или равно нулю и равен –а, если а меньше нуля:
а, если а > 0;
| а |= - а, если а < 0.
Из определения следует, что для любого действительного числа а,
| а | > 0 и | -а | = | а |.

Примеры:
│5│= 5
│2- 6│= - (- 4)=4 так как (2-6) – число отрицательное.
│-8│= -(- 8 )= 8 так как (-8) – число отрицательное.
│2-13│= -(-11)=11, так как (2-13) – число отрицательное.

Решение уравнений:
׀х׀ = а х = а, если а>0 или х = -а, если а<0
׀х - 5׀=6 х-5=6 х=11, х-5=-6 х=-1
׀2х+7׀=-4 ø решений нет.
׀ 7х-49׀=0 7х-49=0 7х=49 х=49:7 х=7

Заключение.
И в заключении я хотел бы сказать, что для досконального изучения материала исследовательская работа подходит лучше всего. Мне представилась возможность больше поработать с интересной, для меня, темой модуля и выйти за рамки того материала, который предоставляет нам учебник 7-го класса. Прочитав и изучив другую литературу, я узнал много нового и, как я считаю, важного для меня.

Продукт проекта
Большое место в математике отведено решение упражнений по теме « Модуль числа». Интерес к теме объясняется тем, что уравнения с модулем предлагаются на школьных экзаменах и при подготовке к ГИА .
С этой целью я подготовил методический сборник для углубленного изучения этого вопроса.

Итогом моего проекта являются:
Мои умения работать с компьютерной техникой;
Мои умения исследовательской работы;
Изучение темы «Модуль» и выход за рамки школьного материала;
Выпуск пособие по математике
для учащихся 7 – 8 классов ,который поможет им при подготовке к ГИА.

Литература:
1.Уравнения и неравенства – Башмаков М. И.
2.Математика Васильев В.В., Соснина Л.И., 2004 год
3. Виленкин Н. Я., Сравнение чисел
4. Сайт http://schoolcollection.marsu.ru/catalog/rubr/eb116c4e-d5ac-41c4-948a-bb438ba..
5.Сайт http://sandbox.openclass.ru/lessons/42384

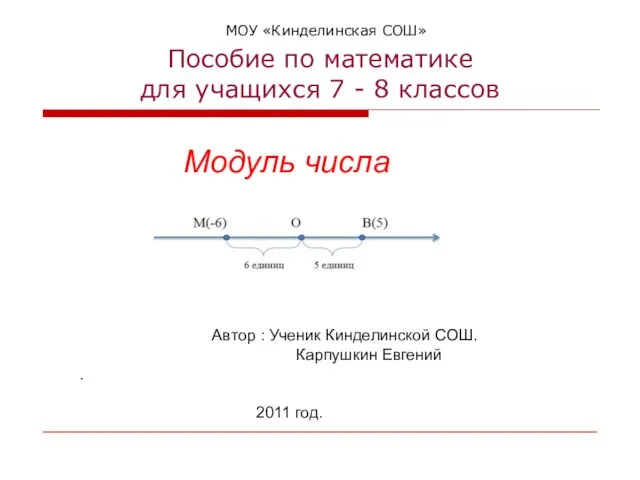
МОУ «Кинделинская СОШ»
Пособие по математике
для учащихся 7 - 8 классов
Модуль числа
Автор : Ученик Кинделинской СОШ.
Карпушкин Евгений
.
2011 год.

Понятие модуля числа

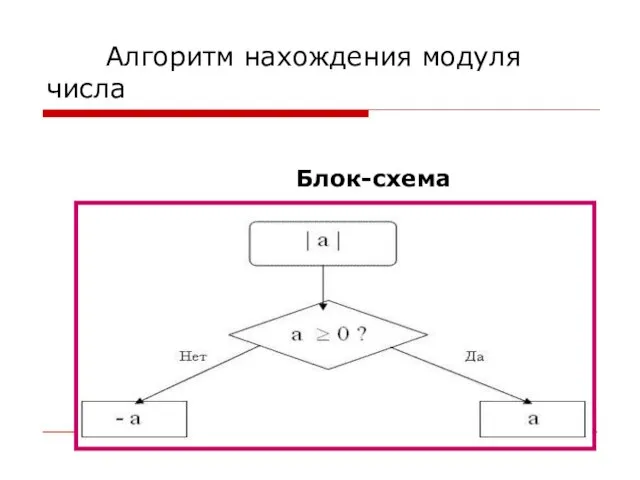
Алгоритм нахождения модуля числа

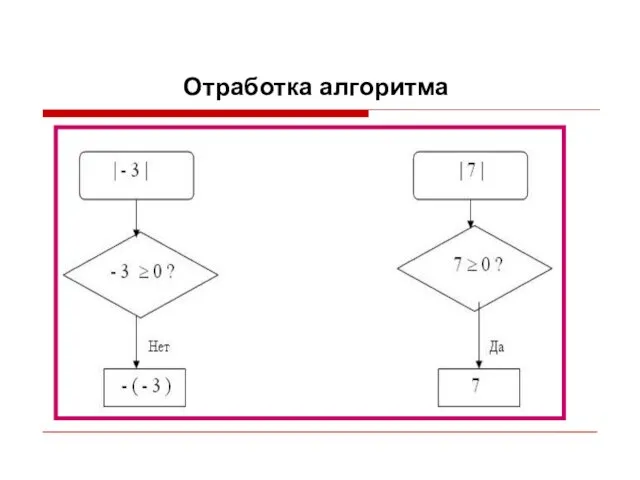
Отработка алгоритма

| 81 | = 81;
| 1,3 | = 1,3;
| – 5,2 | = 5,2;
| 8/9 | = 8/9;
| – 5/7 | = 5/7;
| – 2 9/25 | = 2 9 /25;
| – 52 | = 52;
| 0 | = 0.
| – 8 | – | – 5 | = 8 – 5 = 3 | – 10 | . | – 15 | = 10 . 15 = 150
| 240 | : | – 80 | = 240 : 80 = 3
| 0,1 | . | – 10 | = 0,1 . 10 = 1
Примеры:

Задание 1
1 Найти значения выражений (приготовить карточки):
|-100| , |5+1,1| , |4,4- 8,9| , -|-9,7| , |5-16|
1 Найдите модуль числа
_ 18 10 _ 16
9 2 4
2 Найдите положительное число модуль которого равен:
3 ; 5.
3. Известно,что |a|= 4 Чему равен |-a|?
|a|= 4,6 Чему равен |-a|?
|a|= 3,03 Чему равен |-a|?
4. Выберите из двух чисел, модуль которого меньше:
-5 и 6 2 и -4 -2 и -3
5 Найдите значение выражения:
|0,4| * |-2,5| |-40| * |0,1| |3,6| : |-1,2|

Задание 2

Задание 3
4. Заполни таблицу:
самопроверка по образцу: за 1–2 ошибки – оценка “4”, если нет ошибок – оценка “5”.
5. Сравните:
а) | – 8 | и | – 5 |
б) | 12,3 | и |-11 |
в) | 0 | и | –| 1,5 |

Задание 4
Решите уравнение
а) | х | = 2,5
б) | х | = 0
в) | х | = – 4
г) | а | + 9 = 9
д) | в | – 3 = 33
е) 12,5 – | а | = 10,3
Отметьте на координатной прямой точки, изображающие числа:
а) модуль которых равен 7;
б) модуль которых меньше 7;
в) модуль которых больше 7.

Задание 5
|5х + 3| = 1
|2х - 3| = 1
|х - 5| + |2х –6| = 7
|х² + 3х| – |4 – х| = |х ²- х|
1 ≤ |2х – 1| ≤ 2
х² - 5|х| – 4 ≥ 0
|2х + 5| + |2х – 3| = 8
|х² + 2х| – |2 – х| = |х ²- х|
1 ≤ |3х – 2| ≤ 2
х² - 2|х| – 8 ≥ 0
|(3х + 1)(х – 3)| ≤ 3

Задание 6
Решить уравнения и неравенства
|x|² - 4 = 0
| x|² - 4 < 0 3)
|x|² - 4 > 0
|x|² - 3|x| ≥ 0
|x|² - 3|x| > 0
|x|² - 3|x| ≤ 0
|x|² - 3|x| < 0 В.
x² - 2x + | x| = 0
x² - 2x + | x| < 0
x² - 2x + | x| > 0
|x² - 2x| + x = 0
|x² - 2x| + x < 0

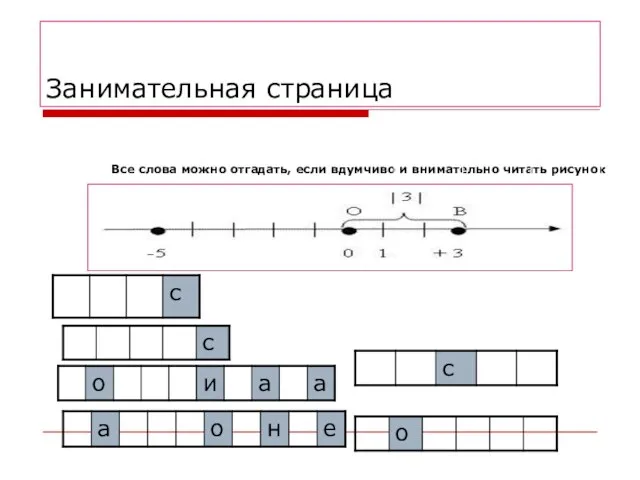
Занимательная страница
Все слова можно отгадать, если вдумчиво и внимательно читать рисунок

Графическое решение уравнений
Под простейшими функциями понимают алгебраическую сумму модулей линейных выражений. Сформулируем утверждение, позволяющее строить графики таких функций, не раскрывая модули ( что особенно важно, когда модулей достаточно много ): "Алгебраическая сумма модулей n линейных выражений представляет собой кусочно- линейную функцию, график которой состоит из n +1 прямолинейного отрезка. Тогда график может быть построен по n +2 точкам, n из которых представляют собой корни внутримодульных выражений, ещё одна -- произвольная точка с абсциссой, меньшей меньшего из этих корней и последняя с абсциссой, большей большего из корней.

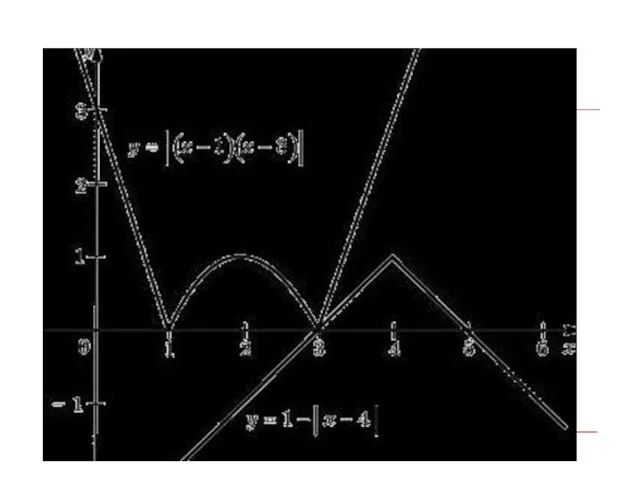
Задание 7 (решение)
Построим графики функций y = |(x–1)(x–3)| и y=1–|x–4 |
1)в y = |(x–1)(x–3)| подставим значен дем пересечение с осью ОХ, для этого решим простое уравнение: 1-|x-4|=0
|x-4|=1
x - 4=1 или x - 4=-1
x=5 x=3
Следовательно данный график пересекает ось ОХ в точках 5 и 3.
При х=4 у=1 и ак видно из графика: графики обеих функций пересекаются в одной точке 3
Ответ: 3

Геометрическая интерпритация (решение)
|x – 1| + |x – 2|=1
с использованием геометрической интерпритации модуля.
Будем рассуждать следующим образом: исходя из геометрической интерпритации модуля, левая часть уравнения представляет собой сумму расстояний от некторой точки абсцисс х до двух фиксированных точек с абсциссами 1 и 2. Тогда очевидно, что все точки с абсциссами из отрезка [1; 2] обладают требуемым свойством, а точки, расположенные вне этого отрезка- нет. Отсюда ответ: множеством решений уравнения является отрезок [1; 2].
Ответ: х  [1; 2]

Построение графиков (решение)
1) f(x)=|x - 1| Вычисляя функции в точках 1, 0 и 2, получаем график, состоящий из двух отрезков(рис.1)
2) f(x)=|x - 1| + |x – 2| Вычисляя значение функиции в точках с абсциссами 1, 2, 0 и 3, получаем график, состоящий из двух отрезков прямых.(рис.2)
3) f(x)=|x - 1| + |x – 2| + |x – 3| Для построения графика вычислим значения функции в точках 1, 2, 3, 0 и 4 (рис.3)
4) f(x)=|x - 1| - |x – 2| График разности строится аналогично графику суммы, то есть по точкам 1, 2, 0 и 3.
См. рис1,2,3,4.

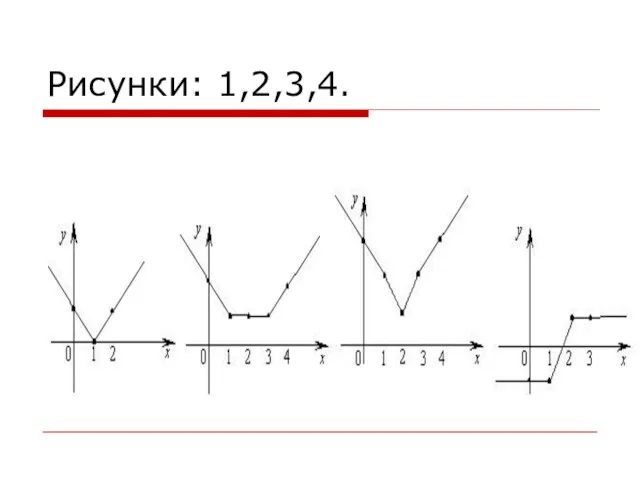
Рисунки: 1,2,3,4.