Презентация на тему Цилиндр, конус, шар

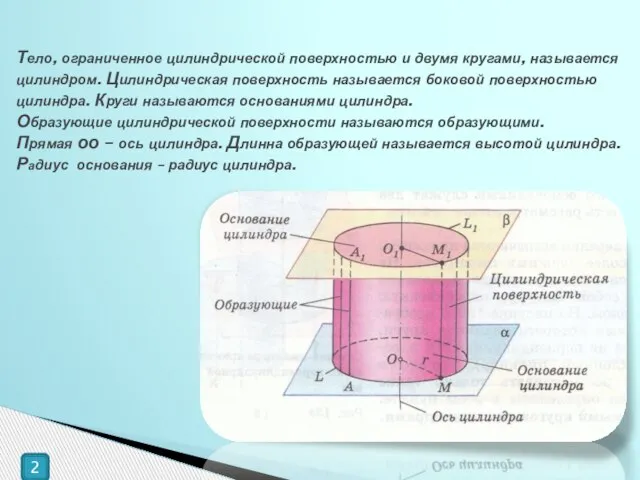
Тело, ограниченное цилиндрической поверхностью и двумя кругами, называется
цилиндром. Цилиндрическая поверхность называется боковой поверхностью цилиндра. Круги называются основаниями цилиндра.
Образующие цилиндрической поверхности называются образующими.
Прямая оо – ось цилиндра. Длинна образующей называется высотой цилиндра.
Радиус основания – радиус цилиндра.
2

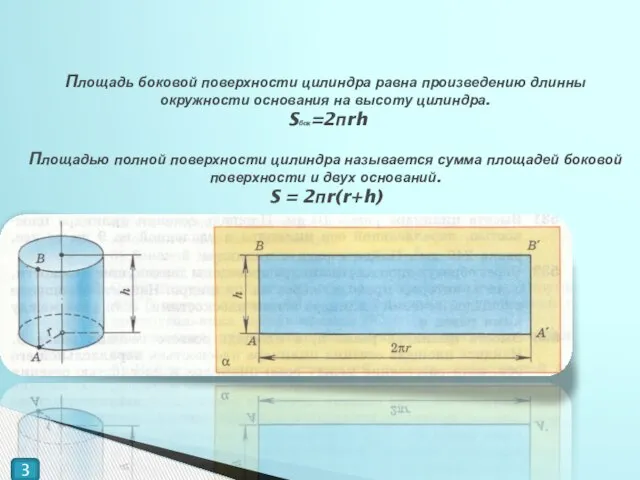
Площадь боковой поверхности цилиндра равна произведению длинны окружности основания на высоту цилиндра. Sбок=2пrh
Площадью полной поверхности цилиндра называется сумма площадей боковой поверхности и двух оснований.
S = 2пr(r+h)
3

Тело, ограниченное конической поверхностью и кругом, называется конусом.
Коническая поверхность называется боковой поверхностью. Круг – основание конуса. Р – вершина конуса. Образующие конической поверхности – образующие конуса. прямая ор – ось конуса. отрезок ор – высота конуса.
4

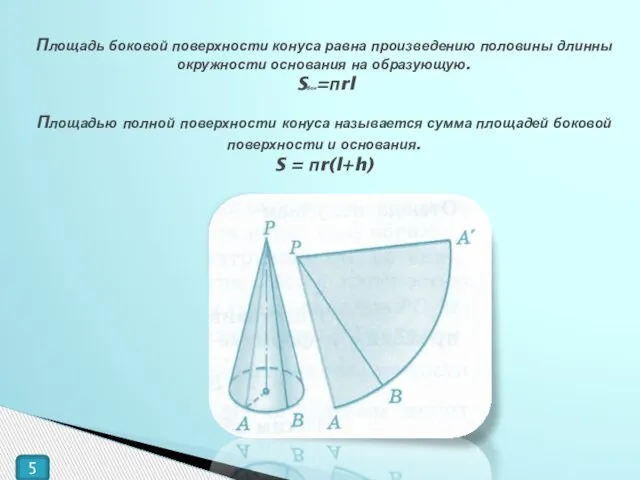
Площадь боковой поверхности конуса равна произведению половины длинны
окружности основания на образующую. Sбок=пrl
Площадью полной поверхности конуса называется сумма площадей боковой поверхности и основания.
S = пr(l+h)
5

Конус, который рассекли плоскостью, параллельной основанию, и убрали верхнюю часть, называется усечённым конусом.
6

Площадь боковой поверхности усечённого конуса равна произведению полусуммы длин
окружностей оснований на образующую.
Sбок=п(r1+r2)l
Площадью полной поверхности усечённого конуса называется сумма площадей боковой поверхности и оснований.
7

Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки. О – центр сферы.
R – радиус сферы. тело, ограниченное сферой – шар.
8

В прямоугольной системе координат уравнение сферы радиусом r с центром с
имеет вид (x-x0)2 + (y-y0)2 + (z-z0)2 = r2
9

Плоскость, имеющая со сферой только одну общую точку , называется касательной к сфере, а их общая точка – точкой касания.
Теорема 1.
радиус сферы, проведённый в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.
Теорема 2.
если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащий на сфере, то эта плоскость является касательной к сфере.
10