Проект по теме:Математические модели реальных процессов в природе и обществе

Мыльные пузыри и математика

Введение
Как соединить два мыльных пузыря, чтобы минимизировать их суммарную площадь поверхности (включая перегородку)? Ответ на этот вопрос интуитивно очевиден, но строгое математическое решение этой задачи было дано лишь в 2000 году. Тот же вопрос для трех и более пузырей до сих пор остается открытым. Немногим лучше обстоит дело и в плоском случае. Несмотря на все достижения математики, геометрия пузырьковых кластеров остается очень сложной задачей.
И мы эту задачу постараемся решить.

Мыльный пузырь
— тонкая пленка мыльной воды, которая формирует шар с переливчатой поверхностью. Мыльные пузыри обычно существуют лишь несколько секунд и лопаются при прикосновении или самопроизвольно. Их часто используют в своих играх дети, но использование пузырей в развлекательных шоу показывает, что и взрослым они тоже нравятся. Из-за недолговечности мыльный пузырь стал синонимом чего-то привлекательного, но бессодержательного и недолговечного.

изопериметрическая задача
Простейшая задача состоит в том, чтобы среди всех плоских замкнутых фигур одинакового периметра (что и дало название всем таким задачам) найти такую, которая охватывает наибольшую площадь.
Чуть иная формулировка той же задачи: среди всех плоских фигур, охватывающих заданную площадь, найти фигуру с наименьшим периметром.
Утверждается, что еще древние греки понимали, что такой фигурой будет окружность.

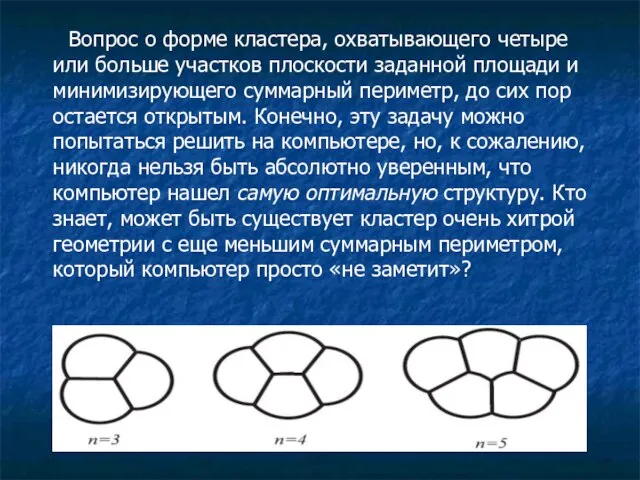
Вопрос о форме кластера, охватывающего четыре или больше участков плоскости заданной площади и минимизирующего суммарный периметр, до сих пор остается открытым. Конечно, эту задачу можно попытаться решить на компьютере, но, к сожалению, никогда нельзя быть абсолютно уверенным, что компьютер нашел самую оптимальную структуру. Кто знает, может быть существует кластер очень хитрой геометрии с еще меньшим суммарным периметром, который компьютер просто «не заметит»?

Еще более удивительна история поиска минимальных поверхностей в трехмерном пространстве — то есть таких замкнутых фигур, которые, охватывая N фиксированных объемов, имеют минимальную площадь поверхности (опять же, тут учитываются как наружные стенки, так и внутренние перегородки). Интуиция подсказывает, что для N = 1 это будет просто сфера, для N = 2 — как бы два слипшихся мыльных пузыря, для N = 3 — три пузыря, слипшихся в виде треугольника и т. д. Однако доказать это математически строго оказывается еще более трудным занятием.

Например, строгое доказательство того, что при заданном объеме сфера действительно обладает минимальной площадью среди всех поверхностей, было дано в 1884 году.
Задача для N = 2 была решена только в 2000 году.
Задача для N = 3 до сих пор остается нерешенной; более того, автор обзора пишет, что, может быть, придется ждать еще сотню лет для получения строгого доказательства.

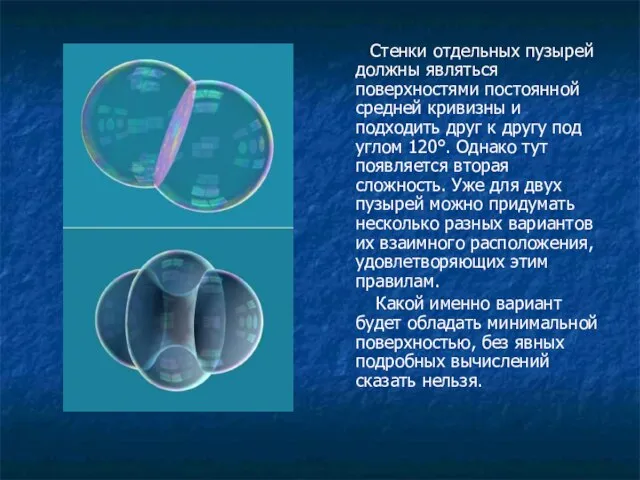
Стенки отдельных пузырей должны являться поверхностями постоянной средней кривизны и подходить друг к другу под углом 120°. Однако тут появляется вторая сложность. Уже для двух пузырей можно придумать несколько разных вариантов их взаимного расположения, удовлетворяющих этим правилам.
Какой именно вариант будет обладать минимальной поверхностью, без явных подробных вычислений сказать нельзя.

МЫЛЬНЫЕ ПУЗЫРИ
ПО-НАУЧНОМУ
Для определения прочности мыльных пузырей (поверхностного натяжения) я использовала весы чашечные (бытовые), набор разновесов (гирьки), песок, нитки, пластилин, небольшой кусок проволоки, а также растворы жидкостей для мытья посуды разной концентрации.

Сначала я попробовала сделать состав, описанный в журнале, но из него пузыри почти не выдувались. Я считаю, что раньше, 100 лет тому назад, было другое мыло, поэтому сейчас этот раствор малоэффективен. Гораздо лучше показали себя современные моющие средства, особенно "Fairy" и "Е". Они дали наилучшие результаты, примерно одинаковые, но "Fairy" в нескольких опытах обошел "Е". Для своих опытов я использовала простую и дистиллированную воду.

Мыльная пленка на простом
проволочном контуре
Мыльные пленки

Теперь подробнее расскажу о способе измерения поверхностного натяжения в мыльной пленке. Нужно сначала закрепить весы, а затем взять проволочку и согнуть ее в двух местах, одинаково удаленных от концов. После этого к центру проволочки прикрепим ниточку, к другому концу нитки - кусочек пластилина. Пластилин (вместе с ниткой и проволочкой) прилепим к одной чаше весов, после чего весы уравновесим. Дальше раствор моющей жидкости поместим под чашей весов с проволочкой так, чтобы проволочка полностью погрузилась в раствор. Потом еще раз все уравновесим и понемногу начнем подсыпать песок в противоположную чашу весов. Как только мыльная пленка на проволочке лопнет, перестанем сыпать песок. После этого взвесим песок и по формуле
=mg/21
найдем поверхностное натяжение (в единицах ньютон/метр), величина которого и определяет прочность мыльного пузыря. А что же касается жизни мыльного пузыря, то все зависит от концентрации раствора - от нескольких секунд до минут! Состав воды тоже влияет на время жизни: например, из соленой воды с моющей жидкостью ничего не выдуешь, а при добавлении глицерина в пресную воду пузыри получаются большие. Мы в кружке попробовали замораживать мыльные пузыри, и эффект превзошел все ожидания. Пузыри покрывались узорами и при прикосновении распадались на половинки. Удивительное зрелище! В этом опыте мы выдували мыльные пузыри на небольшой лоток и просто ставили его на мороз. Советую и вам попробовать!

Иногда возникают интересные и удивительно красивые картины. Возьмем проволочный контур, завязанный в виде простейшего узла – трилистника. При некоторых способах вынимания проволоки из раствора пленка принимает форму листа Мёбиуса. Но чаще полученная пленка состоит из трех гладких полостей с общими «мыльными ребрами», вдоль которых полости выглядят как «книга из трех страниц».

Математическая модель
мыльной пленки
Введем в пространстве систему координат Оxyz. На рисунке изображен контур с натянутой на него пленкой. Пусть проекция поверхности пленки на плоскость xОy есть некоторая область на плоскости; обозначим её G. Проекцию контура Г.
Рассмотрим точку (x, y, z) на поверхности пленки и её проекцию, точку (x, y) в области G.Тогда высота точки на поверхности представляет собой функцию двух переменных: z= (x, y) или z= u(А), где А – точка с координатами (x, y).

Дана функция f (Q),
Q принадлежит проекции Г. Теперь задача состоит в том, чтобы найти значения функции u(А), А принадлежит области G, которая описывает поверхность пленки.
Составим уравнение Лапласа и оно имеет вид:
Для функции u должно выполняться краевое условие

Немного из истории…
Это уравнение было впервые выписано французским математиком П.С. Лапласом (1749-1827) в конце XVIII века.
Краевое условие было поставлено немецким ученым П.Г. Дирихле (1805-1859) уже в середине XIX века, притом не только для уравнения Лапласа, а для любых уравнений с частными производными.

Таким образом нам нужно найти функцию u(А), удовлетворяющую уравнению Лапласа и краевому условию.
Что делать дальше?

Докажем сначала такое утверждение:
в области G существует единственное решение уравнения Лапласа, удовлетворяющее краевому условию.

Однако эта теорема –
теорема существования –
не даёт ответа на вопрос, как найти решение, как построить функцию u.
Исследования еще не закончены, я продолжаю изучать мыльный пузырь!

Заключение
Математика занимается ничем и чем угодно.
Ничем – потому что у неё нет предмета, она имеет дело с несуществующими в реальном мире абстракциями.
Чем угодно – потому что заранее не известно, в какое реальное платье будет одет каркас её абстрактных структур.
Порой математические абстракции не похожи и это вызывает чувство удивления.