Функция f(x) может иметь в этой точке конечную или бесконечную производную f′(x0). Если при переходе через x0 функция меняет направление выпуклости, т.е. существует число δ>0, такое, что на одном из интервалов (x0−δ,x0) или (x0,x0+δ) функция является выпуклой вверх, а на другом − выпуклой вниз, то x0называется точкой перегиба функции y=f(x).
Геометрический смысл точки перегиба состоит в том, что график функции f(x) переходит в этой точке с одной стороны касательной на другую, т.е. кривая и касательная взаимно пересекаются
(рисунок 1).
Другое интересное свойство точки перегиба состоит в том, что график функции f(x) в окрестности точки перегиба x0 расположен внутри одной пары вертикальных углов, образованных касательной и нормалью (рисунок 2).
Необходимое условие существования точки перегиба
Если x0 − точка перегиба функции f(x) и данная функция имеет вторую производную в некоторой окрестности точки x0, причем в точке x0 она непрерывна, то
f′′(x0)=0.
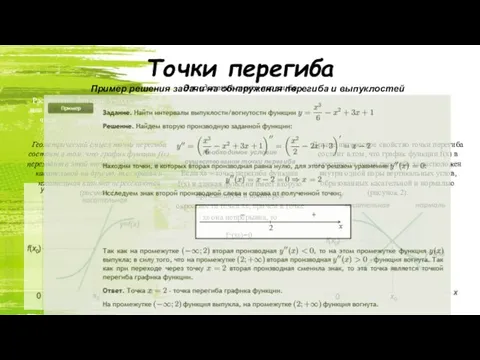
Пример решения задачи на обнаружения перегиба и выпуклостей







 Смысловой конспект презентации
Смысловой конспект презентации Стратегии поведения родителей при поддержке детей в процессе подготовки ГИА
Стратегии поведения родителей при поддержке детей в процессе подготовки ГИА Аганбегян Абел Гезевич
Аганбегян Абел Гезевич Множества. Элемент множества. Подмножества.
Множества. Элемент множества. Подмножества. УРОК 2
УРОК 2 Пошив наволочек
Пошив наволочек Презентация по теме:«ПИЩЕВАРИТЕЛЬНАЯ СИСТЕМА»
Презентация по теме:«ПИЩЕВАРИТЕЛЬНАЯ СИСТЕМА» Хеликс: Автомойка и Шиномонтаж 8
Хеликс: Автомойка и Шиномонтаж 8 Актуальные правовые аспекты синдицированного кредитования
Актуальные правовые аспекты синдицированного кредитования Усовершенствование навыков на спринтерский бег
Усовершенствование навыков на спринтерский бег Длина окружности и площадь круга 5 класс
Длина окружности и площадь круга 5 класс Знакомство с праздником Масленица
Знакомство с праздником Масленица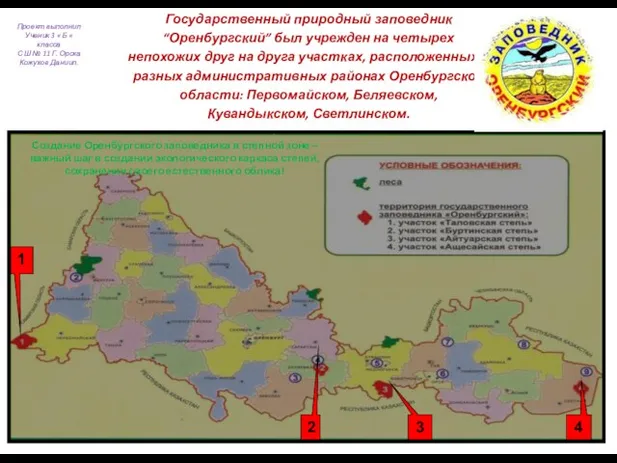 Оренбургский заповедник
Оренбургский заповедник Ценности корпоративной культуры РЭУ
Ценности корпоративной культуры РЭУ Обгрунтування системи охолодження турбо- та гідрогенераторів
Обгрунтування системи охолодження турбо- та гідрогенераторів Взаимосвязь государственной гражданской и муниципальной службы
Взаимосвязь государственной гражданской и муниципальной службы Дегустационные листы
Дегустационные листы Тема любви в повести А.И. Куприна "Гранатовый браслет"
Тема любви в повести А.И. Куприна "Гранатовый браслет" Заработок на облачном майнинге
Заработок на облачном майнинге Решение «Парковка» Обеспечивает: полностью автоматическое управление электромеханическим шлагбаумом, учет и контроль проезда ав
Решение «Парковка» Обеспечивает: полностью автоматическое управление электромеханическим шлагбаумом, учет и контроль проезда ав Новые стандарты – первые шаги
Новые стандарты – первые шаги Фасадное стекло
Фасадное стекло Слово как произведение искусства
Слово как произведение искусства Опера «Кармен» Ж.Бизе
Опера «Кармен» Ж.Бизе Фотоотчет УФМС, Архангельск
Фотоотчет УФМС, Архангельск История космических побед
История космических побед ПРАВА, ОБЯЗАННОСТИ и ОТВЕТСТВЕННОСТЬ ЧЕЛОВЕКА и ГРАЖДАНИНА
ПРАВА, ОБЯЗАННОСТИ и ОТВЕТСТВЕННОСТЬ ЧЕЛОВЕКА и ГРАЖДАНИНА История зарождения баскетбола. Современный баскетбол
История зарождения баскетбола. Современный баскетбол