Производная по направлению и градиент функции

Для характеристики скорости изменения поля в заданном
направлении введём понятие «производной по направлению».
Возьмём в пространстве, где задано поле , некоторую
точку M и найдём скорость изменения функций U при движении точки
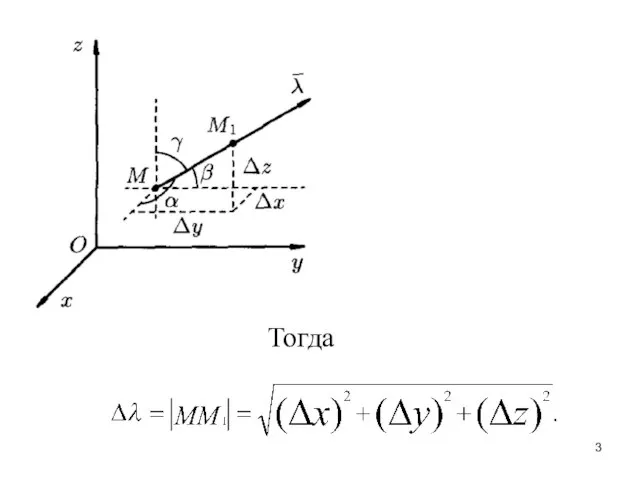
М в произвольном направлении . Пусть вектор имеет начало в точке
M и направляющие косинусы
Приращение функций U, возникающее при переходе от точки к
некоторой точке в направлении вектора определяется
как
или

Тогда

Производной от функции в точке М по направлению
называется предел

Производная по направлению и характеризует скорость изменения
функции (поля) в точке М по этому направлению. Если ,
то функция U возрастает в направлении , если , то функция
U в направлении убывает. Кроме того, величина представляет
собой мгновенную скорость изменения функции U в направлении в
точке М: чем больше , тем быстрее изменяется функция U. В этом
состоит физический смысл производной по направлению.

Переходя к пределу при , получим формулу для вычисления
производной по направлению:

Пример
Найти производную функции в точке в
направлении от этой точки к точке
Решение: Находим вектор и его направляющие косинусы:

Находим частные производные функции и вычисляем их значения в
точке M: