Пропорция

«Геометрия владеет двумя сокровищами: одно из них- теорема Пифагора, другое - деление отрезка в среднем и крайнем отношении.»
И.Кеплер

Человек различает окружающие его предметы по форме. Интерес к форме какого-либо предмета может быть продиктован жизненной необходимостью, а может быть вызван красотой формы. Форма, в основе построения которой лежат сочетание симметрии и золотого сечения, способствует наилучшему зрительному восприятию и появлению ощущения красоты и гармонии. Целое всегда состоит из частей, части разной величины находятся в определенном отношении друг к другу и к целому.
«Невозможно, чтобы две вещи совершенным образом соединились без третьей,… это наилучшим образом может выполнить пропорция.»
Тимей

Отрезок прямой АВ можно разделить на две части следующими способами:
на две равные части – АВ : АС = АВ : ВС;
2) на две неравные части в любом отношении (такие части пропорции не образуют);
3) таким образом, когда АВ : АС = АС : ВС.
Последнее и есть золотое деление или деление отрезка в крайнем и среднем отношении.
Золотое сечение -
гармоничная пропорция
В математике пропорцией называют равенство двух отношений: a : b = c : d. (a*d=b*c)
А
В
С

Понятие золотого сечения
Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему
a : b = b : c или с : b = b : а.
(1-х) : х = х : 1

Число Фидия

A
B
1
1
C
Д
E
K
Деление отрезка в золотом отношении

Кеплер называл золотую пропорцию продолжающей саму себя. «Устроена она так, – писал он, – что два младших члена этой нескончаемой пропорции в сумме дают третий член, а любые два последних члена, если их сложить, дают следующий член, причем та же пропорция сохраняется до бесконечности».
На прямой произвольной длины, отложим отрезок m, рядом откладываем отрезок M. На основании этих двух отрезков выстраиваем шкалу отрезков золотой пропорции восходящего и нисходящего рядов.

История золотого сечения
Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н.э.). Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании.
Леонардо да Винчи также много внимания уделял изучению золотого деления. Он производил сечения стереометрического тела, образованного правильными пятиугольниками, и каждый раз получал прямоугольники с отношениями сторон в золотом делении. Поэтому он дал этому делению название золотое сечение. Так оно и держится до сих пор как самое популярное.

Золотой треугольник
Каждый конец пятиугольной звезды представляет собой золотой треугольник. Его стороны образуют угол 36° при вершине, а основание, отложенное на боковую сторону, делит ее в пропорции золотого сечения.

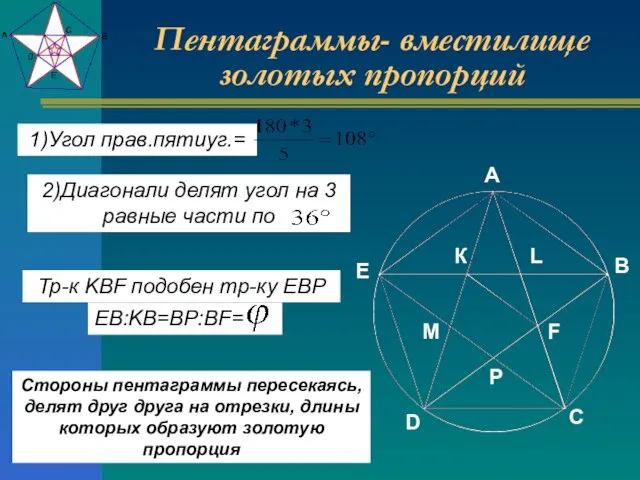
Пентаграммы- вместилище золотых пропорций
EB:KB=BP:BF=
Стороны пентаграммы пересекаясь, делят друг друга на отрезки, длины которых образуют золотую пропорция
Тр-к KBF подобен тр-ку EBP

Соотношения связанные с золотой пропорцией

Соотношения связанные с золотой пропорцией

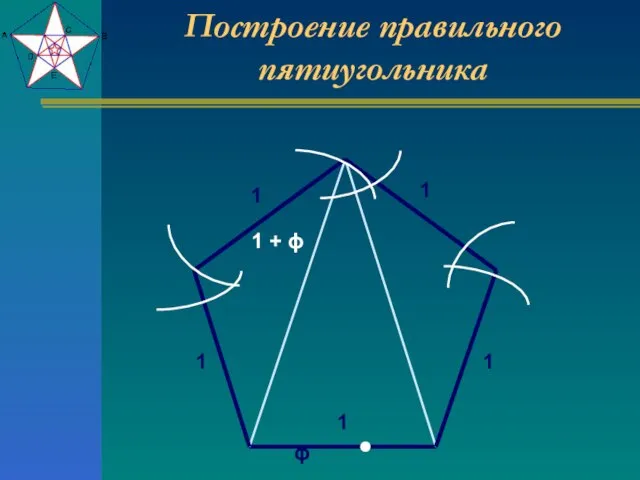
Построение правильного пятиугольника
1
ϕ
1 + ϕ
1
1
1
1

Лука Пачоли «О божественной пропорции»

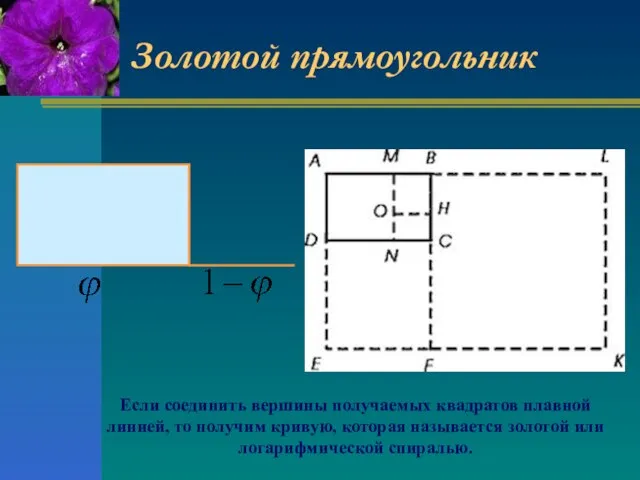
Золотой прямоугольник
Если соединить вершины получаемых квадратов плавной линией, то получим кривую, которая называется золотой или логарифмической спиралью.

Логарифмическая спираль
Логарифмическая спираль единственная из спиралей не меняет своей формы при увеличении размеров. Видимо это свойство послужило причиной того, что в живой природе она встречается чаще других. По логарифмической спирали свёрнуты раковины многих улиток и моллюсков, она встречается в соцветиях растений, даже пауки , сплетая паутину, закручивают нити вокруг центра по логарифмической спирали.

Ряд Фибоначчи
С историей золотого сечения косвенным образом связано имя итальянского математика монаха Леонардо из Пизы, более известного под именем Фибоначчи.
Он много путешествовал по Востоку, познакомил Европу с индийскими (арабскими) цифрами. В 1202 г вышел в свет его математический труд «Книга об абаке» (счетной доске), в котором были собраны все известные на то время задачи. Одна из задач гласила «Сколько пар кроликов в один год от одной пары родится». Размышляя на эту тему, Фибоначчи выстроил такой ряд цифр:

Ряд чисел 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 , … известен как ряд Фибоначчи. Особенность последовательности чисел состоит в том, что каждый ее член, начиная с третьего, равен сумме двух предыдущих 2 + 3 = 5; 3 + 5 = 8; 5 + 8 = 13, 8 + 13 = 21; 13 + 21 = 34 и т.д., а отношение смежных чисел ряда приближается к отношению золотого деления. Так, 21 : 34 = 0,617, а 34 : 55 = 0,618. Это отношение обозначается символом Ф. Только это отношение – 0,618 : 0,382 – дает непрерывное деление отрезка прямой в золотой пропорции, увеличение его или уменьшение до бесконечности, когда меньший отрезок так относится к большему, как больший ко всему.
Свойство чисел ряда Фибоначчи

Золотое сечение и симметрия
Золотое сечение нельзя рассматривать само по себе, отдельно, без связи с симметрией. Великий русский кристаллограф Г.В. Вульф считал золотое сечение одним из проявлений симметрии.
Золотое деление не есть проявление асимметрии, чего-то противоположного симметрии. Согласно современным представлениям золотое деление – это асимметричная симметрия.