Содержание
- 2. Критерий согласия хи-квадрат Пирсона Разработан первоначально для дискретных распределений: Статистический ряд: Нулевая гипотеза: исследуемая случайная величина
- 3. Статистика критерия: Является мерой близости теоретических вероятностей Рl и эмпирических (экспериментальных) частот vl Имеет асимптотическое (при
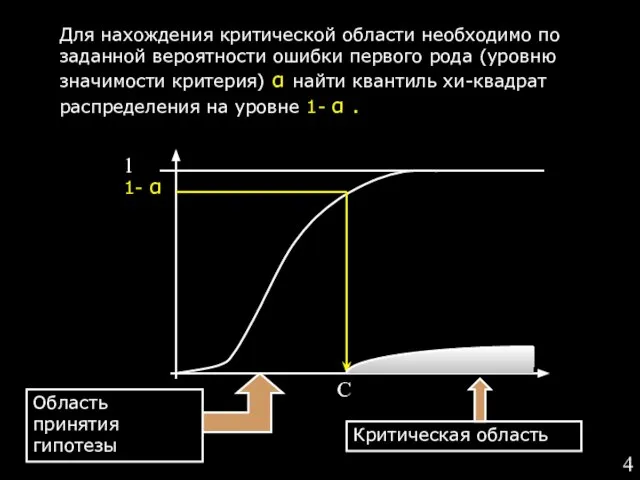
- 4. Для нахождения критической области необходимо по заданной вероятности ошибки первого рода (уровню значимости критерия) α найти
- 5. Подсчитываем значение статистики критерия и сравниваем его с критической точкой. Если То нулевая гипотеза отвергается. В
- 6. Пять шагов проверки гипотезы 1. Сформулировать нулевую H0 и альтернативную H1 гипотезы. 2. Выбрать статистику критерия
- 7. Простейшие параметрические гипотезы Гипотезы о среднем значении гауссовской случайной величины Дано: Проведено две серии независимых испытаний
- 8. Случай 1. Дисперсия известна и равна σ2 Статистика критерия Имеет стандартное распределение
- 10. Скачать презентацию






 Эволюция представлений
Эволюция представлений VI Съезд Подольской ТПП
VI Съезд Подольской ТПП Презентация на тему Азия
Презентация на тему Азия  "Платоновы тела"
"Платоновы тела" Исследовательская работа
Исследовательская работа Диаграммы
Диаграммы Автоматизированная система мониторинга сердечной деятельности
Автоматизированная система мониторинга сердечной деятельности Операции центрального банка на открытом рынке
Операции центрального банка на открытом рынке Тайм-менеджмент
Тайм-менеджмент Презентация к уроку изобразительного искусства Тема: Декоративное рисование. Роспись матрёшки. Составила: учитель началь
Презентация к уроку изобразительного искусства Тема: Декоративное рисование. Роспись матрёшки. Составила: учитель началь In the TV world
In the TV world Единицы измерения времени
Единицы измерения времени Организация системы управления в органах внутренних дел. Тема № 3
Организация системы управления в органах внутренних дел. Тема № 3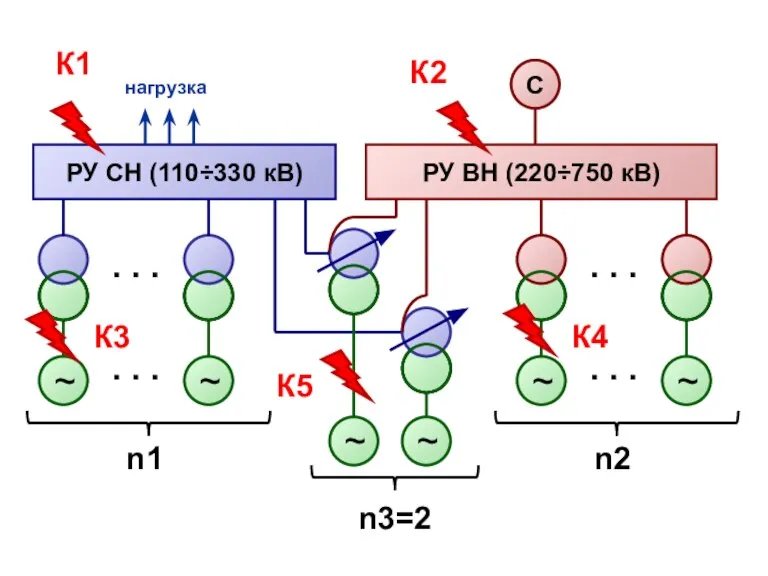 Расчёт ТКЗ схемы замещения
Расчёт ТКЗ схемы замещения История Олимпийских игр Древности
История Олимпийских игр Древности Посадка под школу биохакинга
Посадка под школу биохакинга Вавилонская башня (6 класс)
Вавилонская башня (6 класс) 20141109_narodnye_promysly_rossii
20141109_narodnye_promysly_rossii Особенности влияния «Кортексина» и «Селанка» на процессы ВНД и межполушарные взаимоотношения у ежей
Особенности влияния «Кортексина» и «Селанка» на процессы ВНД и межполушарные взаимоотношения у ежей Урок презентация на тему Логарифмические уравнения
Урок презентация на тему Логарифмические уравнения  Папоротники
Папоротники Древние Оружие Презентация Артема Москалёвагимназия №8 4а класса
Древние Оружие Презентация Артема Москалёвагимназия №8 4а класса Ipsen Aesthetics Russia. Красота и здоровье кожи
Ipsen Aesthetics Russia. Красота и здоровье кожи ОПДП_Виды перевода
ОПДП_Виды перевода НЭИ ДЛЯ ПРОДАВЦА ДЛЯ ПОКУПАТЕЛЯ ДЛЯ ОЦЕНЩИКА
НЭИ ДЛЯ ПРОДАВЦА ДЛЯ ПОКУПАТЕЛЯ ДЛЯ ОЦЕНЩИКА Безработица
Безработица Презентация на тему Олимпийский старт Кубани
Презентация на тему Олимпийский старт Кубани Стратегия дифференциации и определение групп целевых потребителей услуг/продукции УК
Стратегия дифференциации и определение групп целевых потребителей услуг/продукции УК