Содержание
- 2. Ядро Х - материнское; Y - дочернее. Под частицей a в основном понимают α-частицу и β+
- 3. Количество радиоактивных ядер в зависимости от времени подчиняется exp закону: где No - число радиоактивных ядер
- 4. Кроме используют величину среднего времени жизни радиоактивных ядер - По физическому смыслу среднее временя жизни радиоактивных
- 5. Активность Обозначив λN0 как С0, где С0 – активность материала в момент времени t=0, получаем, что
- 6. Если имеется радиоактивное вещество массой M и массовым числом A с постоянной распада λ (или периодом
- 8. Задача 1 Постоянные радиоактивного распада урана, радия и радона соответственно равны 4,9·10-18; 1,37·10-11 и 2,09·10-6 сек-1.
- 9. Задача 2 Найти постоянную распада элемента если его период полураспада равен 1602 лет.
- 10. Задача 3 β-активный изотоп 90Sr (стронций) имеет период полураспада 20 лет. Подсчитать какая доля первоначального количества
- 11. Задача 4 Какая доля первоначальноного количества ядер радиоактивного препарата со средним временем жизни τ: останется через
- 12. Решение Число ядер препарата к моменту времени t: N(t)=N0exp(-t/ τ) Доля ядер, оставшихся к моменту t=10τ,
- 13. Задача 5 Вычислить постоянную распада, среднее время жизни и период полу распада радиоактивного нуклида, активность которого
- 14. Активность по определению – число распадающихся ядер в единицу времени: А=dNd /dt где Nd – число
- 15. Задача 6 Определить возраст древних деревянных предметов, у которых удельная активность 14С составляет 3/5 удельной активности
- 16. Решение Радиоактивный углерод 14С, период полураспада которого Т1/2 = 5730 лет, непрерывно образуется в верхних слоях
- 17. Задача 7 Свежеприготовленный препарат содержит 1,4 мкг радиоактивного нуклида 24Nа. Какую активность он буде иметь через
- 18. Решение Согласно С(t) = λ·N0·e-λt = С0e -λt, 1 а. е. м. ≈ 1,660 540 2∙10−27
- 19. Задача 8 Определить число радиоактивных ядер в свежеприготовленном препарате 82Br, если известно, через сутки его активность
- 20. Решение
- 23. Эквивалентная доза
- 25. Скачать презентацию






















 Реактивный двигатель ,
Реактивный двигатель , Проблемы и перспективы «дачной амнистии»: взгляд экспертов
Проблемы и перспективы «дачной амнистии»: взгляд экспертов Государство, его признаки и формы
Государство, его признаки и формы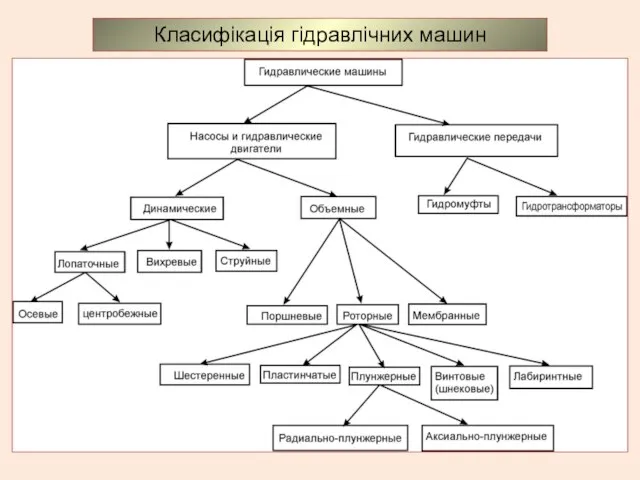 Класифікація гідравлічних машин
Класифікація гідравлічних машин Образы в социальной рекламе
Образы в социальной рекламе Турция
Турция К ВОПРОСУ О РЕГИОНАЛЬНОМ ТЕЛЕМЕДИЦИНСКОМ ЦЕНТРЕСАНКТ-ПЕТЕРБУРГА(ТМЦ СПБ)
К ВОПРОСУ О РЕГИОНАЛЬНОМ ТЕЛЕМЕДИЦИНСКОМ ЦЕНТРЕСАНКТ-ПЕТЕРБУРГА(ТМЦ СПБ) Ежегодно команда юношей принимает участиев межрегиональных соревнованиях среди кадетских корпусов, православных гимназий, дет
Ежегодно команда юношей принимает участиев межрегиональных соревнованиях среди кадетских корпусов, православных гимназий, дет одготовка специалистов для работы с лицами с ОВЗ в Норвегии
одготовка специалистов для работы с лицами с ОВЗ в Норвегии Применение анкерного крепления и хим. упрочнения кровли в условиях Ярегского месторождения
Применение анкерного крепления и хим. упрочнения кровли в условиях Ярегского месторождения Путешествие в город огород
Путешествие в город огород Презентация на тему Духовная жизнь
Презентация на тему Духовная жизнь Питание растений
Питание растений Нормативно-правовые основы и финансово-хозяйственные механизмы перехода на новую систему финансирования
Нормативно-правовые основы и финансово-хозяйственные механизмы перехода на новую систему финансирования Спорт — это здорово
Спорт — это здорово Лев Николаевич Толстой
Лев Николаевич Толстой Prince2 - структурированный метод управления проектами в социальной сфере
Prince2 - структурированный метод управления проектами в социальной сфере Кайнозойская эра
Кайнозойская эра Все профессии важны, с математикой дружны
Все профессии важны, с математикой дружны Физиология, биохимия микроорганизмов (прокариотов: бактерий, эукариотов: простейших, грибов, вирусов)
Физиология, биохимия микроорганизмов (прокариотов: бактерий, эукариотов: простейших, грибов, вирусов) Парад Профессий - ХХI век. Автор Сохибкулова Марина
Парад Профессий - ХХI век. Автор Сохибкулова Марина Trinkgeld für azubis
Trinkgeld für azubis Семинар FCI для судей IGP
Семинар FCI для судей IGP Многогранники
Многогранники Чем интересны музеи
Чем интересны музеи "Пожарные
"Пожарные ОПТИМИЗАЦИЯ ШКОЛЬНОГО САЙТА
ОПТИМИЗАЦИЯ ШКОЛЬНОГО САЙТА к 8 марта с музыкой
к 8 марта с музыкой