Различные доказательства теоремы Пифагора

Теорема Пифагора

Структура задачи
Дано
Что нужно доказать
Доказательство

CAB–прямоугольный треугольник
A
B
c
Дано:

Доказать: SBAED=SFGAC+SHCBI
Построим нужные нам квадраты
на сторонах треугольника:
Пусть BAED - квадрат, постро -
енный на гипотенузе прямоуголь-
ного треугольника CAB.
А FGAC и HCBI -квадраты, построен-
ные на его катетах.

Доказательство

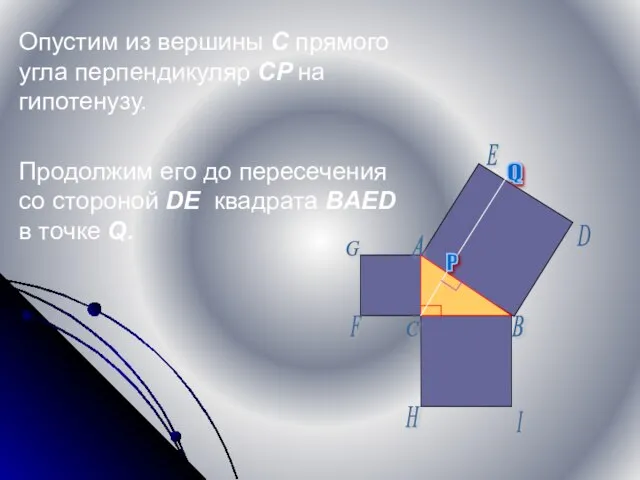
Опустим из вершины С прямого угла перпендикуляр CP на гипотенузу.
Продолжим его до пересечения со стороной DE квадрата BAED в точке Q.
A
B
C
D
E
F
G
H
I
Q
P

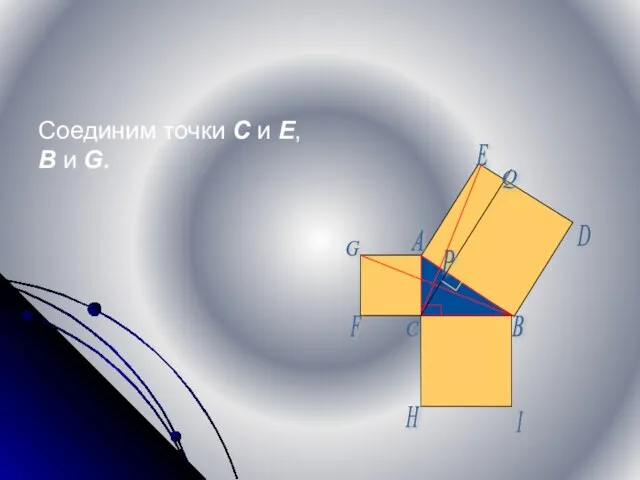
Соединим точки C и E, B и G.
B
C
D
E
F
G
H
I
Q
P
A

Получили треугольники CAE и BGA.
A
B
C
D
E
F
G
H
I
Q
P

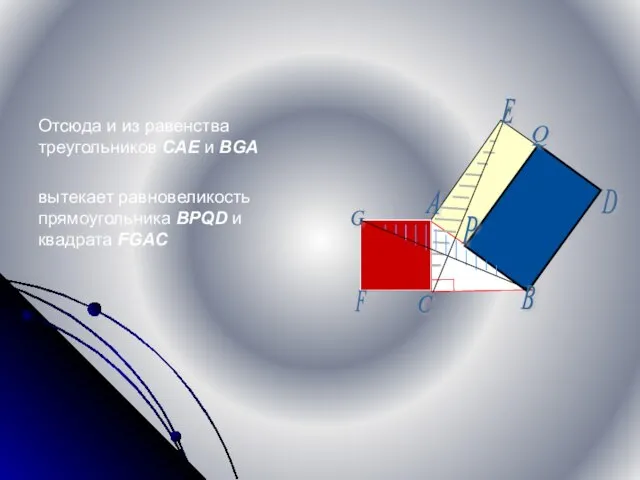
Очевидно, что углы CAE=GAB(=A+90°);
Отсюда следует, что треугольники CAE и BGA(заштрихованные на рисунке) равны между собой (по двум сторонам и углу, заключённому между ними).
D
Q
P
B
E
F
G
C
A

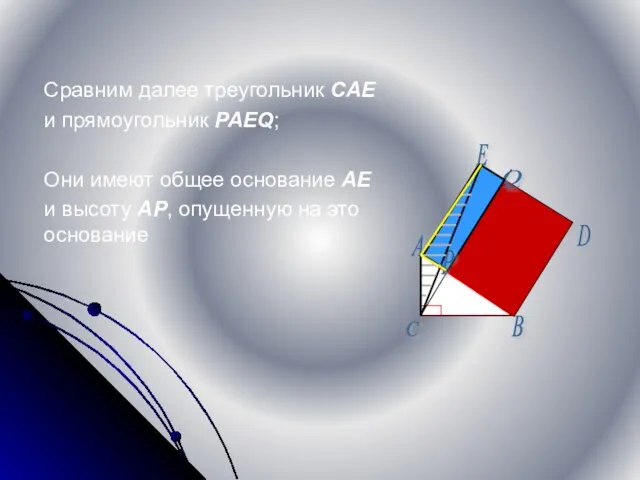
Сравним далее треугольник CAE
и прямоугольник PAEQ;
Они имеют общее основание AE
и высоту AP, опущенную на это основание
A
B
C
D
E
Q
P

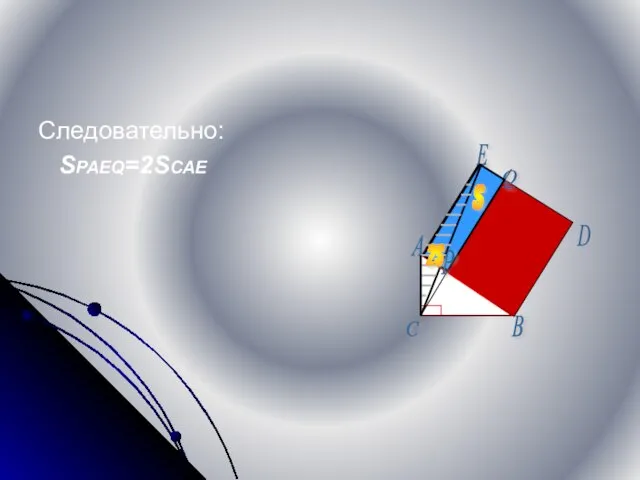
Следовательно:
SPAEQ=2SCAE
A
B
C
D
E
Q
P
S
2S

Точно так же квадрат FGAC
и треугольник BGA
имеют общее основание GA
высоту AC
Значит SFGAC=2SBGA
A
C
F
G
B
S
2S

Отсюда и из равенства треугольников CAE и BGA
вытекает равновеликость прямоугольника BPQD и квадрата FGAC
D
Q
P
G
F
A
C
E
B

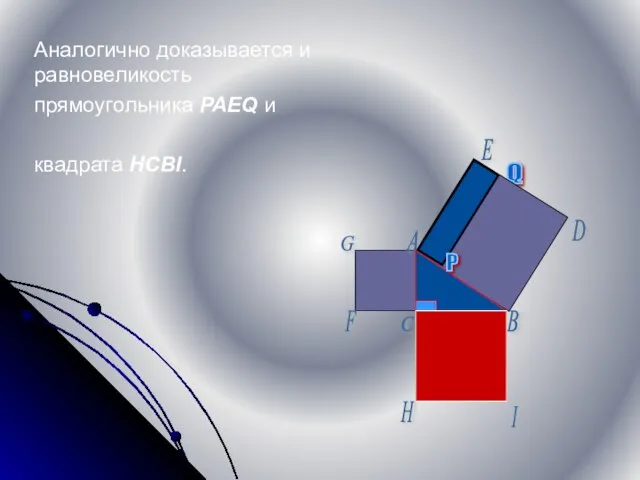
Аналогично доказывается и равновеликость
прямоугольника PAEQ и
квадрата HCBI.
Q
P