Вычисление площадей плоских фигур с помощью определенного интеграла

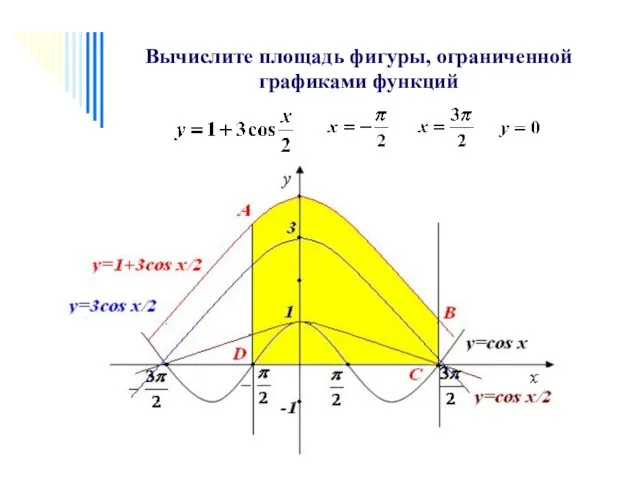
Вычислите площадь фигуры, ограниченной графиками функций

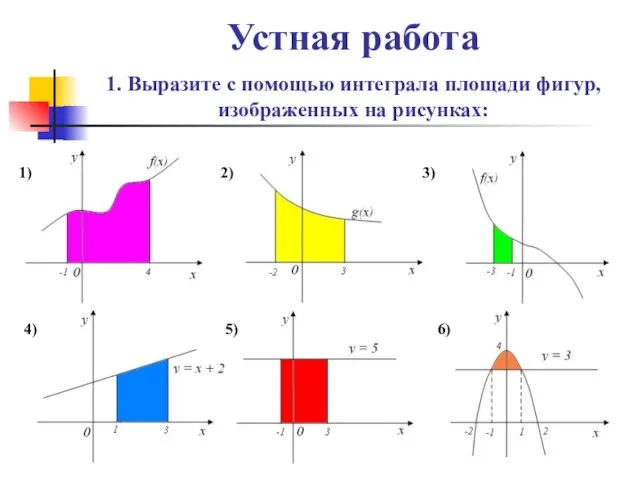
Устная работа
1. Выразите с помощью интеграла площади фигур, изображенных на рисунках:
1)
2)
3)
4)
5)
6)

2. Вычислите интегралы:
1).
2).
3).
4).
10,5
1
64
1

Немного истории
«Интеграл» придумал Якоб Бернулли (1690г.)
«восстанавливать» от латинского integro
«целый» от латинского integer
от латинского
primitivus – начальный,
ввел
Жозеф Луи Лагранж
(1797г.)
«Примитивная функция»,

Интеграл в древности
Этот метод был подхвачен и развит Архимедом, и использовался для расчёта площадей парабол и приближенного расчёта площади круга.
Евдокс Книдский
Архимед
Первым известным методом для расчёта интегралов является метод исчерпания Евдокса (примерно 370 до н. э.), который пытался найти площади и объёмы, разрывая их на бесконечное множество частей, для которых площадь или объём уже известен.

Исаак Ньютон
(1643-1727)
Наиболее полное изложение дифференциального и интегрального исчислений содержится в
«Методе флюксий...»
(1670–1671, опубликовано в 1736).
Переменные величины - флюенты(первообразная или неопределенный интеграл)
Скорость изменения флюент – флюксии (производная)

Лейбниц Готфрид Вильгельм
(1646-1716)
впервые использован Лейбницем в конце
XVII века
Символ образовался из буквы
S — сокращения слова
summa (сумма)

Определенный интеграл
И. Ньютон
Г. Лейбниц
где
Формула Ньютона - Лейбница

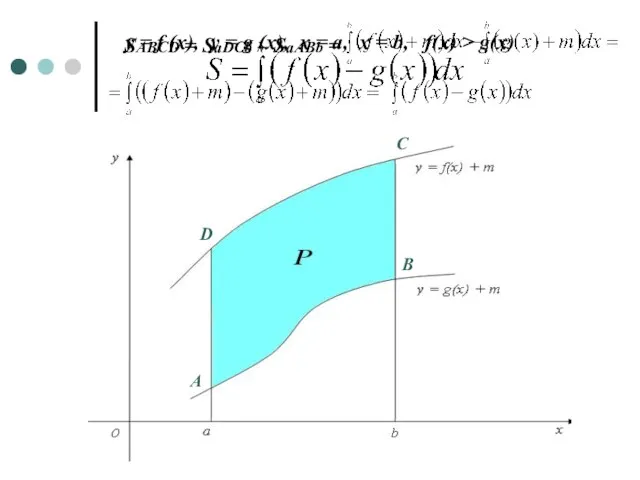
y = f (x), y = g (x), x = a, x = b, f(x) > g(x)
A
B
C
D
SABCD = SaDCb – SaABb =

Пример. Вычислите площадь фигуры,
ограниченной линиями y = x, y = 5 – x, x = 1, x = 2.
x
y
0
1
2
5
5
y = x
y = 5 - x
A
B
C
D

Задание1. Вычислите площадь фигуры, ограниченной линиями
y = 3 – x2,
y = 1+ | x |
y = 1 + |x|
y
х
0
1
1
-1
3
y = 3 – х2
S1
S2
S = S1 + S2

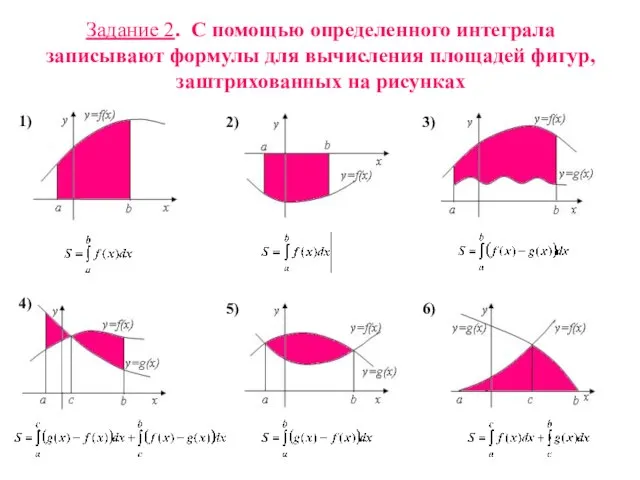
Задание 2. С помощью определенного интеграла записывают формулы для вычисления площадей фигур, заштрихованных на рисунках
1)
2)
3)
4)
5)
6)

Подберите из данных формул для вычисления площади фигуры ту, которая подходит к одному из шести чертежей.
S1 =
S2 =
S3 =
S4 =
S5 =
S6 =
5
1
2
3
4
6

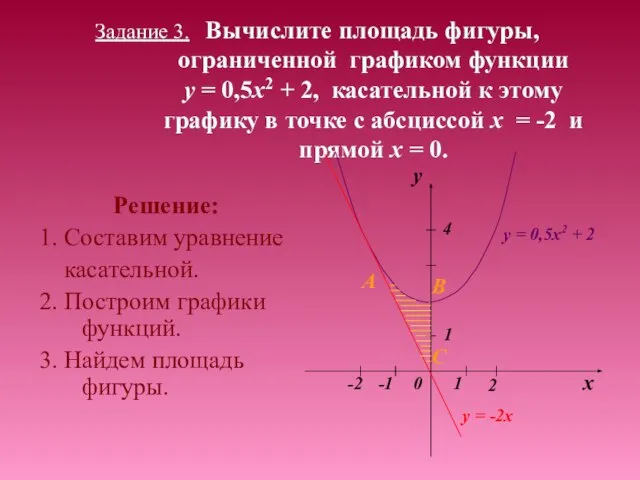
Задание 3. Вычислите площадь фигуры, ограниченной графиком функции
y = 0,5x2 + 2, касательной к этому
графику в точке с абсциссой х = -2 и прямой х = 0.
Решение:
1. Составим уравнение
касательной.
2. Построим графики функций.
3. Найдем площадь фигуры.
х
y
0
-1
1
-2
1
4
у = -2х
у = 0,5х2 + 2
А
B
C
2

Итоги урока