Разложение многочлена на множители способом группировки

План урока:
1. Проверка домашнего задания
2. математический бой
3. письмо от астрономов
4. письмо от археологов
5. письмо от работников Берлинского музея.
6. итог урока

Ответы домашнего задания
№716(в,г)
an2+cn2-ap+ap2-cp+cp2=(an2-ap+ap2)-(cn2-cp+cp2)=a(n2-p+p2)-c(n2-p+p2)=(n2-p+p2)(a-c)
xy2-by2-ax+ab+y2-a=(xy2-by2+y2)-(ax-ab+a)=y2(x-b+1)-a(x-b+1)=(x-b+1)(y2-a)
№718(в,г)
a2-5a+4=a2-(4a+a)+4=a2-4a-a+4=(a2-a)-(4a-4)=a(a-1)-4(a-1)=(a-4)(a-1)
a2-6a-16=a2-8a+2a-16=(a2+2a)-(8a+16)=a(a+2)-8(a+2)=(a+2)(a-8)

Девиз урока:
Три пути ведут к знанию: путь размышления – это путь самый благородный, путь подражания – это путь самый легкий и путь опыта – это путь самый горький.
Конфуций.

Математический бой
Соедините линиями соответствующие части определения
Разложение много-
члена на
множители - это
Представление многочлена в виде
Суммы двух или нескольких много –
членов
Представление многочлена в виде
произведения двух или нескольких
одночленов
Представление многочлена в виде
Произведения двух или нескольких
многочленов
Математический бой
Математический бой

Завершить утверждение
Представление многочлена в виде произведения одночлена и многочлена называется ………

Восстановить порядок действий
чтобы разложить многочлен на множители способом группировки, нужно
1
2
3
Вынести в каждой группе
общий множитель за скобки
в виде многочлена
Сгруппировать его члены так,
чтобы слагаемые в каждой
группе имели общий множитель.
Вынести в каждой группе
общий множитель за скобки
в виде многочлена

В адрес Академии пришло письмо от астрономов, исследующих поверхность Марса.

Соедините линиями многочлены с соответствующими им способами разложения.
Вынесение множителя за
скобки
Не раскладывается на
множители
Способ группировки

Соедините линиями соответствующие части определения (оценка - 2 балла)
Разложение много-
члена на
множители - это
Представление многочлена в виде
Суммы двух или нескольких много –
членов
Представление многочлена в виде
произведения двух или нескольких
одночленов
Представление многочлена в виде
Произведения двух или нескольких
многочленов

Завершить утверждение
(оценка 2 балла)
Представление многочлена в виде произведения одночлена и многочлена называется вынесением общего множителя за скобки

Восстановить порядок действий
чтобы разложить многочлен на множители способом группировки, нужно (2 балла)
1
2
3
Вынести в получившемся
выражении
общий множитель за скобки
в виде многочлена
Сгруппировать его члены так,
чтобы слагаемые в каждой
группе имели общий множите.
Вынести в каждой группе
общий множитель за скобки
в виде многочлена

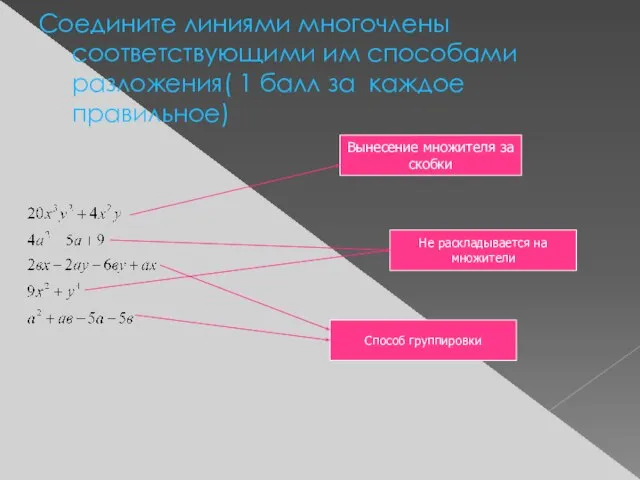
Соедините линиями многочлены соответствующими им способами разложения( 1 балл за каждое правильное)
Вынесение множителя за
скобки
Не раскладывается на
множители
Способ группировки

Археологи , исследуя гробницы Египта , обнаружили в одной из пирамид дверь , для открытия которой нужно разгадать код.
Помогите
археологам

Разложите на множители(устно)
x(a + 3)- y(a +3 ) 12b(c + x) +12(c + x)
5b(a + b) +a +b 4a – 4b + ax – bx ab + bc +12a +12c

Просматривая старые архивы, работники Берлинского музея обнаружили обрывки рукописи, которые вам предстоит восстановить.

Подведение итогов
Какая задача стояла перед нами в начале урока?
Можно ли считать, что мы ее решили?

Дифференцированные задания по уровням
А.Задания нормативного уровня. 1балл за 1пример
1)7а-7в+аn-bn (a – b)(7 + n)
2)xy+2y+2x+4 (y + 2)(x + 2)
3)y2a – y2b + x2a – x2b (a – b)(y2 + x2 )
Б Задания компетентного уровня 2баллa за 1пример
1) xy + 2y – 2x -4 (x +2)(y – 2)
2)2cx – cy – 6x + 3y (2x –y)(c – 3)
3)x2 + xy + xy2 + y3 (x + y)(x + y2 )
С. Задания творческого уровня 3 балл x a за 1пример
x4 + x3y – xy3 – y4 (x + y)(x3 - y3 )
xy2 – by2 – ax + ab + y2 – a (y2 - a)(x – b + 1)
x2 – 3x + 6 – 2x (x – 2)(x – 3)

Оценочная таблица
«5»- 18-20 баллов
«4»- 15-17 баллов
«3»- 11-14 баллов
«2»- менее 10 баллов

Домашнее задание
Повторить пункт 30, №711(д,е) 716(а)