Содержание
- 2. При решении уравнений, в вычислениях бывает удобно заменить многочлен произведением нескольких многочленов. Такое представление называют разложением
- 3. Алгоритм отыскания общего множителя нескольких одночленов 1. Найти наибольший общий делитель коэффициентов всех одночленов, входящих в
- 4. Пример 1. Разложить на множители: -x4y3-2x3y2+5x2. Воспользуемся сформулированным алгоритмом. 1. Наибольший общий делитель коэффициентов –1, -2
- 5. Пример 2. Разложить на множители многочлен 36a6b3-96a4b4+64a2b5 . Займемся вынесением общего множителя за скобки. Рассмотрим коэффициенты
- 6. Пример 3. Разложить на множители а4x4+x2a2+a4
- 7. Пример 4. Разложить на множители 6n3+3n2+12n.
- 8. Пример 5. Решить уравнение 12x2 +3x=0. Вынесем за скобки 3х. Получим 3х(4х+1)=0. Произведение равно нулю, когда
- 9. Пример 6. Представить в виде произведения сумму: В этой сумме каждое слагаемое содержит множитель х-3у. Этот
- 10. ОСНОВНЫЕ РЕЗУЛЬТАТЫ Мы ввели новое (для вас) понятие математического языка: разложение многочлена на множители. Вы познакомились
- 11. Попробуй решить самостоятельно те задания, которые здесь были разобраны : Разложить на множители: -x4y3-2x3y2+5x2 , 36a6b3-192a4b4+64a2b5
- 12. Безошибочного вынесения за скобки общего множителя!
- 14. Скачать презентацию











 Соединение боковых срезов пижамной сорочки запошивочным швом
Соединение боковых срезов пижамной сорочки запошивочным швом 3.Классификация проектов
3.Классификация проектов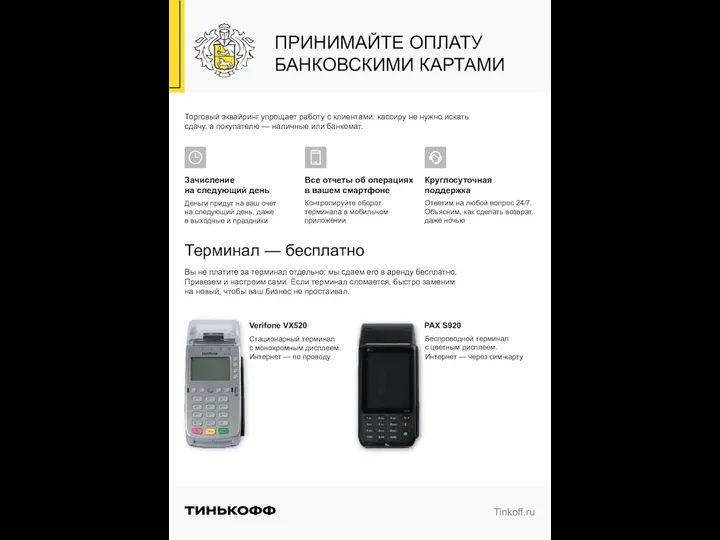 Онлайн кассы
Онлайн кассы Презентация на тему Спартанская и Афинская системы обучения и воспитания в Древней Греции
Презентация на тему Спартанская и Афинская системы обучения и воспитания в Древней Греции  Примеры тоталитарных режимов
Примеры тоталитарных режимов Инновационная экономика и технологическое предпринимательство
Инновационная экономика и технологическое предпринимательство Практические аспекты мониторинга программ
Практические аспекты мониторинга программ Question1
Question1 ЭУП «Основы правовых знаний»
ЭУП «Основы правовых знаний» Аппарат для приготовления и продажи кислородных коктейлей. Создание вендинговой сети.
Аппарат для приготовления и продажи кислородных коктейлей. Создание вендинговой сети. 1
1 The National Gallery
The National Gallery Заседание рабочей группы по подготовке к введению комплексного учебного курса «Основы религиозных культур и светской этики» в о
Заседание рабочей группы по подготовке к введению комплексного учебного курса «Основы религиозных культур и светской этики» в о Открытый Кубок Донецкой области по маунтенбайку-2011
Открытый Кубок Донецкой области по маунтенбайку-2011 Презентация на тему Колебательный контур
Презентация на тему Колебательный контур Начало Первой мировой войны. Роль Восточного фронта в войне
Начало Первой мировой войны. Роль Восточного фронта в войне Sh_Mimi_Mishki_memori_avt_v_kontse_slova_Ch3
Sh_Mimi_Mishki_memori_avt_v_kontse_slova_Ch3 Презентация на тему Эвакуация населения
Презентация на тему Эвакуация населения  Проблема снижения уровня тревожности детей на занятиях физическим воспитанием
Проблема снижения уровня тревожности детей на занятиях физическим воспитанием Презентация на тему Этапы коррекционно-педагогической деятельности и коррекционные дневники
Презентация на тему Этапы коррекционно-педагогической деятельности и коррекционные дневники Понятия групповой психотерапии. История
Понятия групповой психотерапии. История Государственная (итоговая) аттестация выпускников 9-х классов
Государственная (итоговая) аттестация выпускников 9-х классов Кедровые орешки«Лесные Угодья»
Кедровые орешки«Лесные Угодья» Окно
Окно Технологическая платформа «Малая распределенная энергетика»
Технологическая платформа «Малая распределенная энергетика» Что такое эмблемы
Что такое эмблемы Локомотивные технические средства регулирования и обеспечения безопасности движения поездов КЛУБ и КЛУБ-У. При организации движе
Локомотивные технические средства регулирования и обеспечения безопасности движения поездов КЛУБ и КЛУБ-У. При организации движе Тема 1. Энергия и энергоэффективность в мире труда и профессии Услуги с помощью энергии, виды энергии, энергоэффективность Мате
Тема 1. Энергия и энергоэффективность в мире труда и профессии Услуги с помощью энергии, виды энергии, энергоэффективность Мате