Разнообразные подходы к решению текстовых задач

Цель методической разработки:
систематизация различных подходов к изучению раздела математики по решению текстовых задач, используемых на уроках математики в 5-6 классах, алгебры в 7-11 классах.

Задачи:
Проведение теоретического анализа различных подходов к решению задач в современной науке.
Обобщение различных приемов решения текстовых задач.
Обобщение методики решения задач на движение, работу, проценты, смеси, сплавы и т.д.
Определение сложностей, которые испытывают учащиеся при решении текстовых задач, и пути их решения.

Основные цели решения текстовых задач в школьном курсе математики:
научить переводить реальные предметные ситуации в различные математические модели,
обеспечить действенное усвоение учащимися основных методов и приемов решения учебных математических задач.

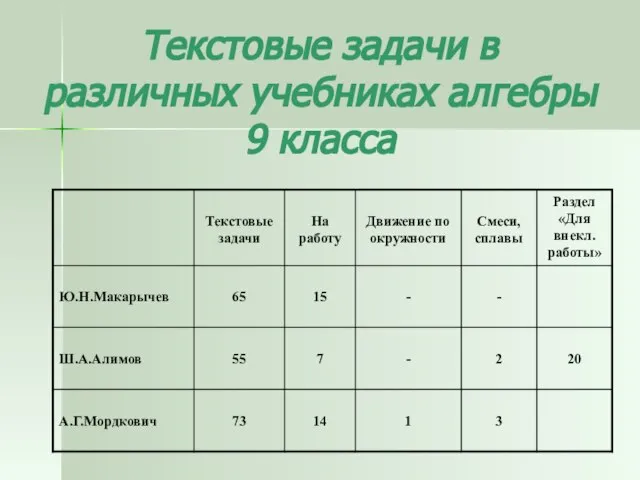
Текстовые задачи в различных учебниках алгебры 9 класса

Этапы решения
текстовых задач:
Анализ содержания задачи.
Поиск пути решения задачи и составление плана ее решения.
Осуществление плана решения задачи.
Проверка решения задачи.

Приемы, используемые
на этапе «Анализ задачи»
представление той жизненной ситуации, которая описана в задаче. Цель такого воспроизведения — выявление основных количественных и качественных характеристик ситуации, представленной в задаче.
постановка специальных вопросов и поиск ответов на них — включает следующий «стандартный» набор вопросов, ответы на которые позволяют детально разобраться в содержании задачи: О чем говорится в задаче? Что известно в задаче? Что требуется найти в задаче? Что в задаче неизвестно? и др.
переформулировка текста задачи — состоит в замене данного в задаче описания некоторой ситуации другим описанием, сохраняющим все отношения, связи, но более явно их выражающим. При необходимости строится вспомогательная модель задачи: краткая запись условия, таблица, рисунок, чертеж и т.п.
моделирование ситуации, описанной в задаче, с помощью реальных предметов, предметных моделей или графических моделей.

Приемы, используемые
на этапе «Поиск пути решения задачи и составление
плана ее решения».
анализ задачи по тексту или по ее вспомогательной модели;
от вопроса задачи к данным (аналитический путь) или от данных к вопросу (синтетический путь);
комбинированный (анализ и синтез), анализ часто производят «про себя»;
разбиение задачи на смысловые части;
введение подходящих обозначений в том случае, когда данные (или искомые) в задаче не обозначены.

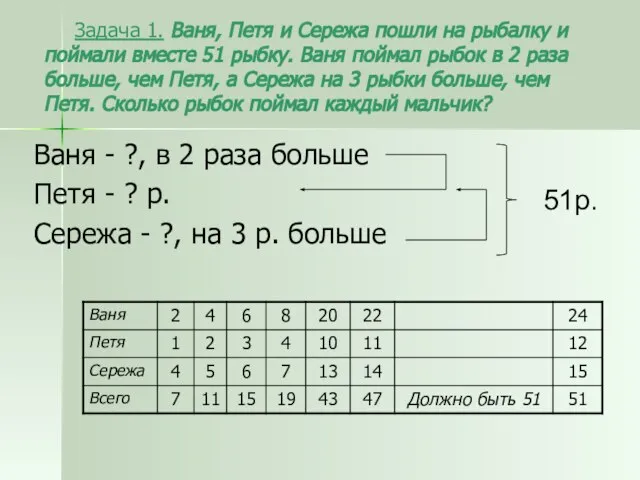
Задача 1. Ваня, Петя и Сережа пошли на рыбалку и поймали вместе 51 рыбку. Ваня поймал рыбок в 2 раза больше, чем Петя, а Сережа на 3 рыбки больше, чем Петя. Сколько рыбок поймал каждый мальчик?
Ваня - ?, в 2 раза больше
Петя - ? р.
Сережа - ?, на 3 р. больше
51р.

Пусть
х + 2х + х +3 =51.
х = 12.
Следовательно,
Петя поймал 12 рыбок,
Ваня 24 рыбки,
Сережа 15 рыбок.

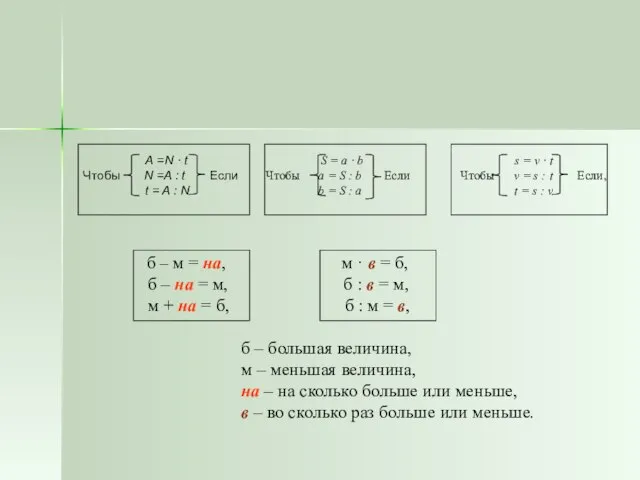
Алгоритм
Обозначим неизвестную величину через х.
Выразим через нее другие величины.
Найдем зависимость между ними и на основании ее составим уравнение.
Решим уравнение.
Найдем ответ на вопрос задачи.
Проверим правильность решения задачи.
Запишем ответ.

А =N · t
Чтобы N =A : t Если
t = A : N
s = v · t
Чтобы v = s : t Если,
t = s : v
S = a · b
Чтобы a = S : b Если
b = S : a
б – м = на, м · в = б,
б – на = м, б : в = м,
м + на = б, б : м = в,
б – большая величина,
м – меньшая величина,
на – на сколько больше или меньше,
в – во сколько раз больше или меньше.

Задача 2. Пристани А и В расположены на реке, причем В – на 80 км ниже по течению, чем А. Катер прошел путь из А в В и обратно за 8 ч 20 мин. За какое время катер прошел расстояние от А до В и расстояние от В до А, если известно, что скорость в стоячей воде равна 20 км/ч?
Р е ш е н и е.
Первый этап.
Составление математической модели.
Пусть х км/ч – скорость течения реки.
Получим уравнение
+ = .
Второй этап. Работа с составленной моделью.
Решив уравнение, находим х = 4.
Третий этап. Ответ на вопрос задачи.
= 3 ч, = 5 ч.

Задача 3. Двое рабочих выполнили вместе некоторую работу за 12 ч. Если бы сначала первый рабочий сделал половину этой работы, а затем другой остальную часть, то вся работа была бы выполнена за 25 ч. За какое время мог бы выполнить эту работу каждый рабочий в отдельности?
Р е ш е н и е.
Первый этап. Составление математической модели.
Примем всю работу за 1.
Производительность труда I рабочего
, а II - . За 12 ч, работая отдельно, I
рабочий выполнит ·12 всей работы, а II рабочий - ·12
всей работы, т.е. + = 1
ч – время, которое потребуется I рабочему, чтобы сделать половину работы, ч – время, которое потребуется II рабочему, чтобы сделать половину работы, тогда + = 25.
Второй этап. Работа с составленной моделью. Решив систему
+ = 1,
+ = 25; находим решение: х = 20, у = 30 .
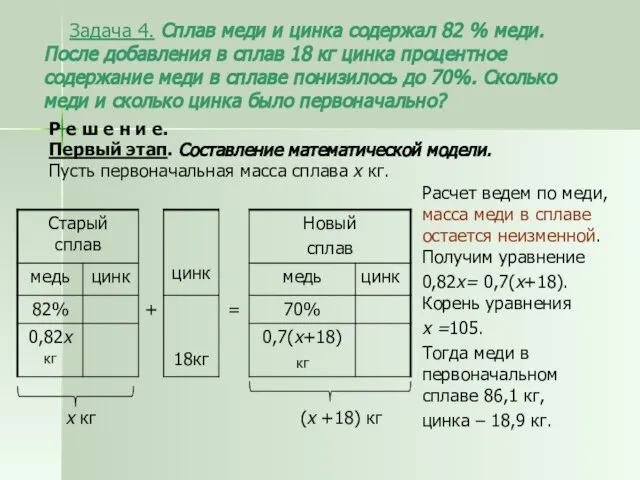
Третий этап. Ответ на вопрос задачи. 20 ч и 30 ч.

Задача 4. Сплав меди и цинка содержал 82 % меди. После добавления в сплав 18 кг цинка процентное содержание меди в сплаве понизилось до 70%. Сколько меди и сколько цинка было первоначально?
Расчет ведем по меди, масса меди в сплаве остается неизменной. Получим уравнение
0,82х= 0,7(х+18). Корень уравнения
х =105.
Тогда меди в первоначальном сплаве 86,1 кг,
цинка – 18,9 кг.
Р е ш е н и е.
Первый этап. Составление математической модели.
Пусть первоначальная масса сплава х кг.

Сложности при решении
текстовых задач
составление математической модели
составление уравнений и неравенств,
связывающих данные величины и переменные,
которые вводят учащиеся
нахождение соответствия между различными
величинами, применительно к которым формулируется
вопрос задачи
решение уравнений, системы уравнений
или неравенств

Сложности при решении текстовых задач и
пути их решения.
Составление математической модели
непонимание физических, химических,
экономических терминов, законов,
зависимости
непонимание связи между расстоянием,
скоростью и временем при равномерном
движении или между работой,
производительностью труда и временем
и т.п.
затруднения в определении скорости
сближения объектов при движении
навстречу, в одном направлении или
при движении по окружности
Тщательно изучить и
правильно истолковать
содержание задачи,
выразив искомые
величины через
известные величины и
введенные переменные.
Не зацикливаться на
периодичности маршрута
при движении по
окружности, а мыслить
только в категориях
время, путь, скорость.

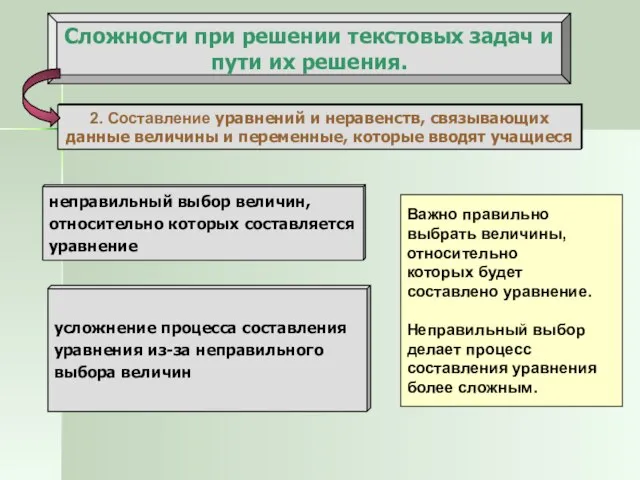
Сложности при решении текстовых задач и
пути их решения.
2. Составление уравнений и неравенств, связывающих
данные величины и переменные, которые вводят учащиеся
неправильный выбор величин,
относительно которых составляется
уравнение
усложнение процесса составления
уравнения из-за неправильного
выбора величин
Важно правильно
выбрать величины,
относительно
которых будет
составлено уравнение.
Неправильный выбор
делает процесс
составления уравнения
более сложным.

Сложности при решении текстовых задач и
пути их решения.
3. Нахождение соответствия между различными
величинами, применительно к которым
формулируется вопрос задачи
большое количество неизвестных,
нахождение значения которых
не являются необходимыми
Держать в поле зрения
основную цель, не боясь
вводить столько
вспомогательных
переменных, сколько их
понадобится по ходу
решения.
Совсем необязательно
ставить в качестве
непременного условия
сведение числа
неизвестных к
минимуму.
невозможность нахождения значения
переменных, которые в уравнениях
присутствуют и не являются
необходимыми

Сложности при решении текстовых задач и
пути их решения.
4. Решение уравнений, системы уравнений или неравенств
невозможность решения уравнения,
неравенства или их системы
решение уравнения, неравенства или
их системы нерациональным способом
Решение полученной
системы уравнений или
неравенств желательно
наиболее рациональным
методом.

Задача: Два тела, двигаясь по окружности в одном и том же направлении, встречаются через каждые 56 мин. Если бы они двигались с теми же скоростями в противоположных направлениях, то встречались бы через каждые 8 мин. Если при движении в противоположных направлениях в некоторый момент времени расстояние по окружности между телами равно 40 м, то через каждые 24 с оно будет 26 м (в течение этих 24 с тела не встретятся).
Найдите скорости тел и длину окружности.

х
у
Пусть l м – длина окружности,
х м/мин - скорость первого тела, а у м/мин – скорость второго тела (х > у).
В задаче речь идет о трех ситуациях, каждую из которых можно описать уравнением.
Решение:
Задача: Два тела, двигаясь по окружности в одном и том же направлении, встречаются через каждые 56 мин. Если бы они двигались с теми же скоростями в противоположных направлениях, то встречались бы через каждые 8 мин. Если при движении в противоположных направлениях в некоторый момент времени расстояние по окружности между телами равно 40 м, то через каждые 24 с оно будет 26 м ( в течении этих 24 с тела не встретятся).
Найдите скорости тел и длину окружности.

При движении в одном направлении первое тело догоняет второе со скоростью
(x – y) м/мин.
После одного из обгонов следующий обгон имеет место через столько минут, сколько понадобиться, чтобы преодолеть l метров со скоростью (x – y) м/мин, т.е. через 56 мин:
= 56 (1)

При движении в разных направлениях тела сближаются со скоростью (x + y) м/мин,
причем l м они вместе проходят за 8 мин
= 8 (2)
Если первоначальное расстояние было равно 40м, осталось пройти до встречи 26 м, то общий путь составляет
40м – 26м = 14м.
Он был преодолен со скоростью (x + y) м/мин за 24 с, т.е. за мин, что равно мин.

Следовательно последняя часть условия приводит к уравнению = (3)
Разделив уравнение (2) на (1), получим
= , отсюда у = х.
Решим систему уравнений
у = ¾ х
=
Следовательно, у = 15, а из уравнения (2) l = 280.
Ответ: 280 м, 20 м/мин, 15 м/мин.
=>
х = 20

Выводы:
Для того, чтобы научиться решать задачи, надо приобрести опыт их решения путем многократного повторения операций, действий, составляющих предмет изучения.
Редкие ученики самостоятельно приобретают такой опыт. Долг учителя - помочь учащимся приобрести опыт решения задач, научить их решать задачи.
Помощь учителя не должна быть чрезмерной, но и не быть слишком малой.
Навыки решения текстовых задач формируются на основе осмысленных знаний и умений.
Для формирования навыков нужна тщательно продуманная система упражнений и задач «от простого к сложному».
Знания учащихся по математике должны совершенствоваться с решением каждой новой задачи.
Следует добиваться, чтобы осознанные умения и навыки ученики получали при наименьших затратах времени.
Следует учитывать индивидуальные особенности и возможности учащихся.
.