Содержание
- 2. Задача наискорейшего обнаружения разладки Разладка − скачкообразное изменение свойств временного ряда, которое происходит в неизвестный момент
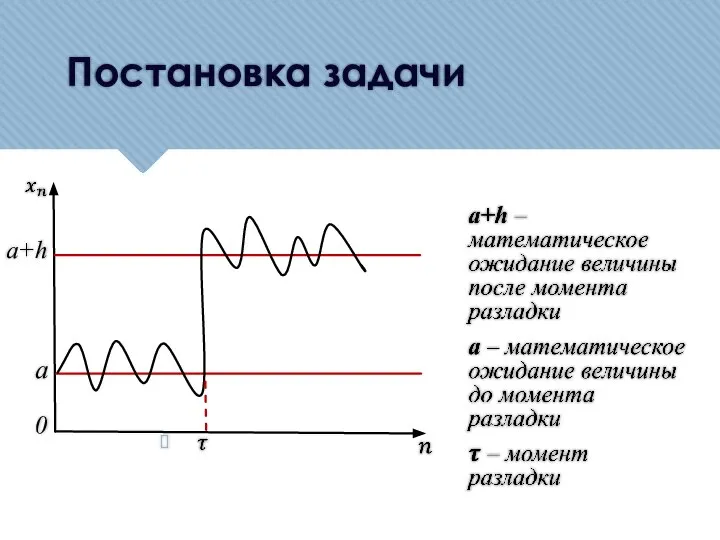
- 3. Постановка задачи
- 4. Практическое применение Текущий контроль любого технологического процесса; обнаружение утечек из продуктопровода; отслеживание текущего технического состояния газопровода
- 5. Задачи 1. Изучить литературу по тематике работы. 2. Реализовать методы обнаружения моментов разладки: метод кумулятивных сумм
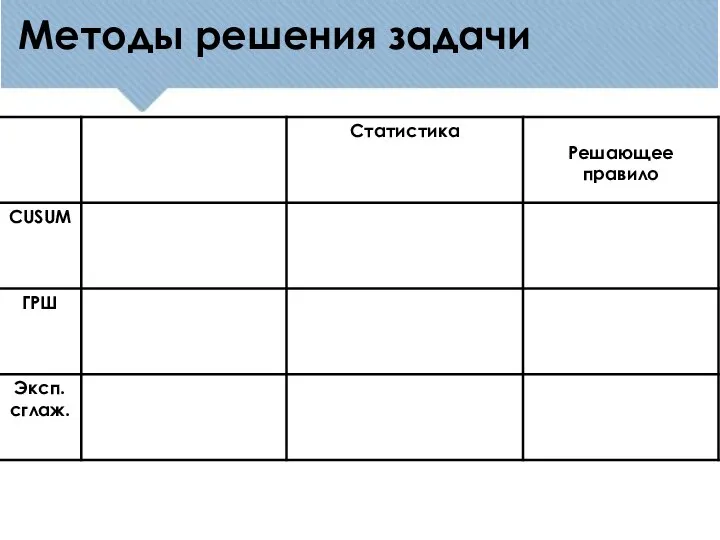
- 6. Методы решения задачи
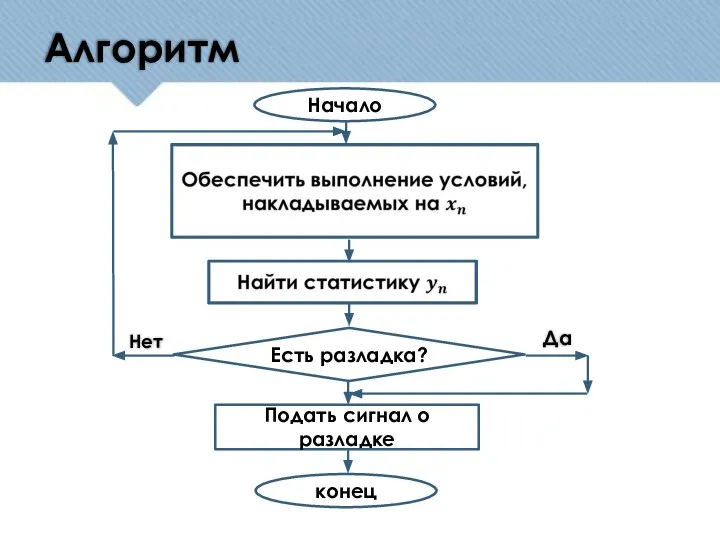
- 7. Алгоритм Да Нет
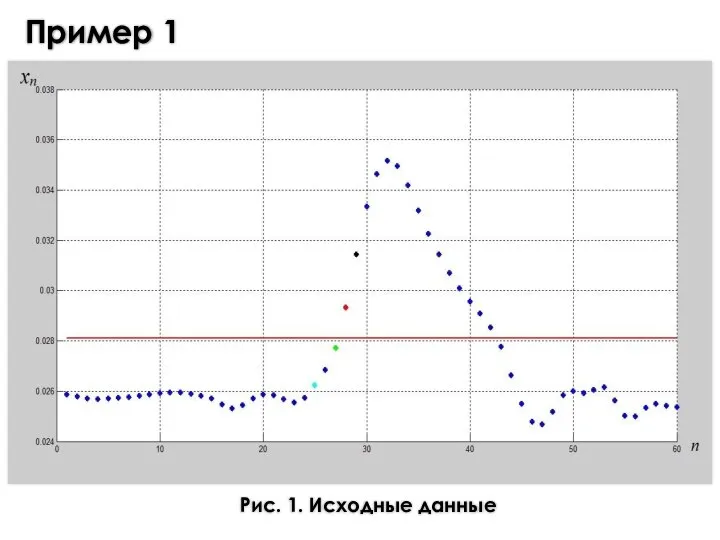
- 8. Пример 1 Рис. 1. Исходные данные
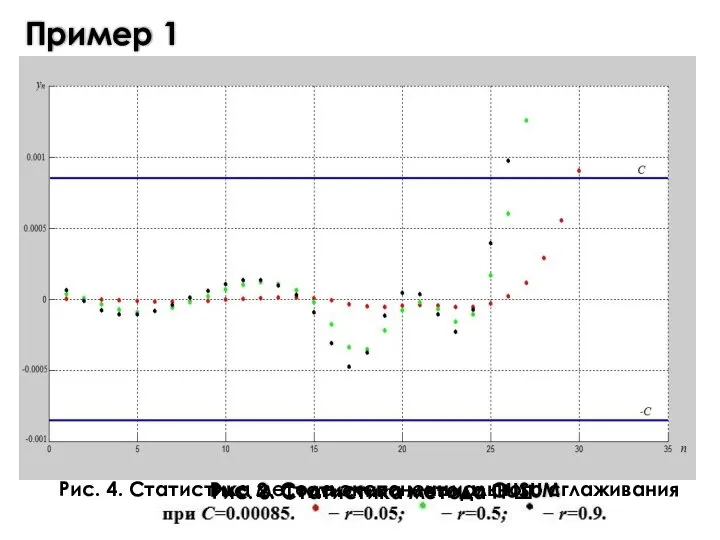
- 9. Пример 1 Рис. 2. Статистика метода CUSUM Рис. 3. Статистика метода ГРШ Рис. 4. Статистика метода
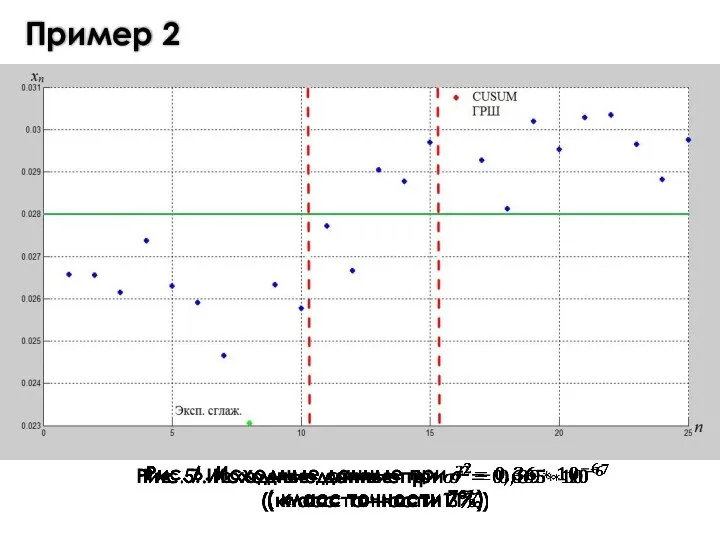
- 10. Пример 2
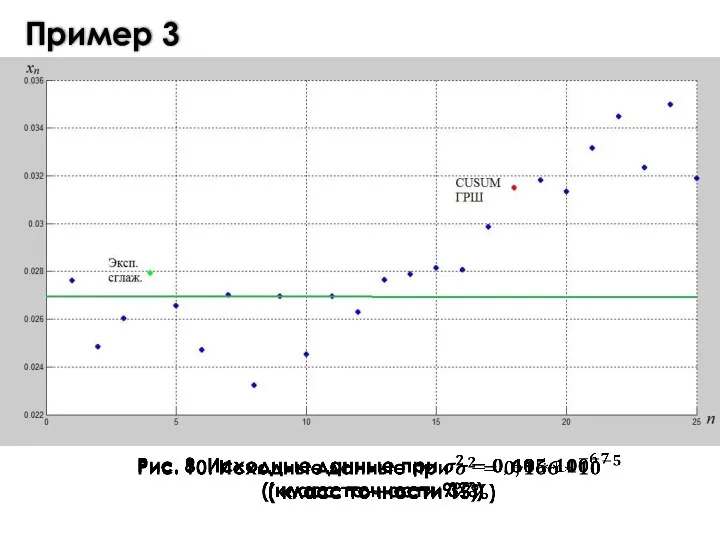
- 11. Пример 3
- 12. Выводы Результаты зависят от настроек алгоритмов; Чем меньше дисперсия, тем точнее работают методы; Преимущество метода экспоненциального
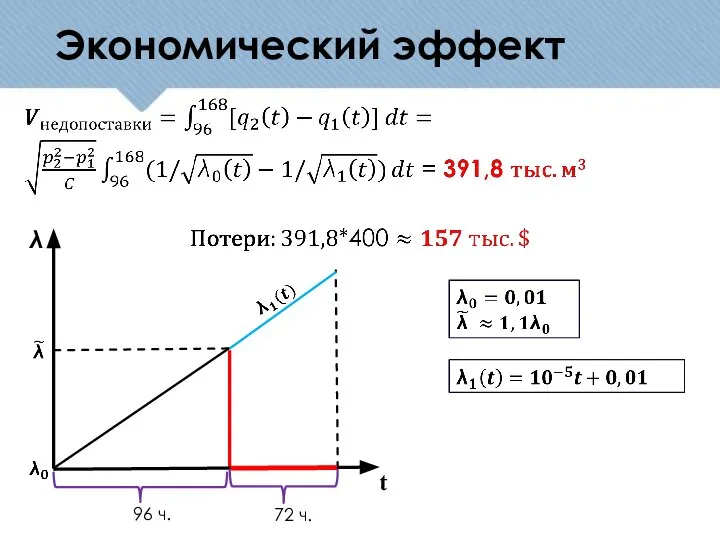
- 13. Экономический эффект
- 14. Заключение Проведен анализ существующих методов. Исследованы непараметрические методы последовательного анализа: CUSUM, ГРШ, экспоненциального сглаживания. Рассмотрены результаты
- 16. Скачать презентацию




 Презентация на тему Водные ресурсы. Безопасное использование и охрана
Презентация на тему Водные ресурсы. Безопасное использование и охрана Презентация на тему Физика твердого тела. Рост и дефекты кристаллов
Презентация на тему Физика твердого тела. Рост и дефекты кристаллов
 Презентация на тему Технология моделирования в начальной школе
Презентация на тему Технология моделирования в начальной школе Самостоятельные занятия физическими упражнениями
Самостоятельные занятия физическими упражнениями Права ребёнка
Права ребёнка Риск и промышленная безопасность
Риск и промышленная безопасность  Фрукты, которые растут на деревьях
Фрукты, которые растут на деревьях Какие бывают дома?
Какие бывают дома? Устройство и техническое обслуживание автомобилей классификация грузовых автомобилей
Устройство и техническое обслуживание автомобилей классификация грузовых автомобилей Лес Инвест Трейдинг
Лес Инвест Трейдинг Отцовская доблесть. Семья Канчуриных
Отцовская доблесть. Семья Канчуриных Воздействие тепловых двигателей на окружающую среду
Воздействие тепловых двигателей на окружающую среду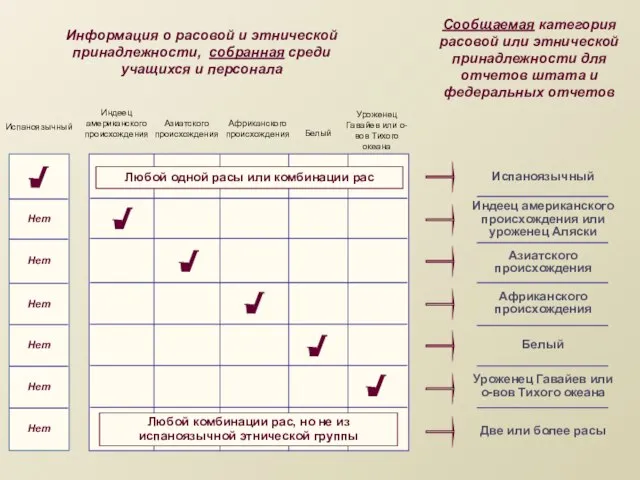 Информация о расовой и этнической принадлежности, собранная среди учащихся и персонала
Информация о расовой и этнической принадлежности, собранная среди учащихся и персонала Бизнес-модель Остервальдера как основной инструмент бизнес-моделирования
Бизнес-модель Остервальдера как основной инструмент бизнес-моделирования Экономия с лампочкой Ilumia Classical
Экономия с лампочкой Ilumia Classical Города РоссииНовосибирск
Города РоссииНовосибирск Решение уравнений высоких степеней
Решение уравнений высоких степеней Слова с сочетаниями ЖИ-ШИ
Слова с сочетаниями ЖИ-ШИ Социальная карта Башкортостана
Социальная карта Башкортостана Викторина
Викторина «Цветок. Строение и функции цветка и его частей»
«Цветок. Строение и функции цветка и его частей» Понятие об общении
Понятие об общении Заочная экскурсия по мемориальному комплексу «ХАТЫНЬ»
Заочная экскурсия по мемориальному комплексу «ХАТЫНЬ» Инструменты автоматизации форматирования. Перекрестные ссылки. Сортировка
Инструменты автоматизации форматирования. Перекрестные ссылки. Сортировка Бюджетная система
Бюджетная система ООО «ЯнаулВодоканал»РБ г. Янаул, ул. Обьездная,17тел. (34760)
ООО «ЯнаулВодоканал»РБ г. Янаул, ул. Обьездная,17тел. (34760) HP StorageWorksX9000 Network Storage Systems
HP StorageWorksX9000 Network Storage Systems Окружность и круг (9 класс)
Окружность и круг (9 класс)