Relații. Proprietăți. Operații. Relații remarcabile

Df. Fiind date două mulțimi A și B vom numi produs cartezian și vom notă prin A × B, mulțimea tuturor perechilor ordonate de elemente din A și B definită astfel:
A × B = {(a, b): a ∈ A, b ∈ B}.
Fiind dată o a treia mulțime C putem construi următoarele produse carteziene:
(A × B) × C = {((a, b), c): a ∈ A, b ∈ B, c ∈ C}
A × (B × C) = {(a, (b, c)): a ∈ A, b ∈ B, c ∈ C}
A × B × C = {(a, b, c): a ∈ A, b ∈ B, c ∈ C}
Elementele produslui cartezian de forma A1 × A2 × ... × An se numesc n-upluri ordonate.
Mulțimile A1, A2, ..., An se numesc factorii produsului cartezian, iar elementele a1, a2,...,an se numesc coordonatele (sau proiecțiile) elementului (a1, a2, ..., an).
În cazul când A1 = A2 = ... = An = A putem nota A1 × A2 × ... × An cu An.
Adică, A2 = A × A; A3 = A × A × A; An = A × A × ... × A (de n ori).
Produs cartezian

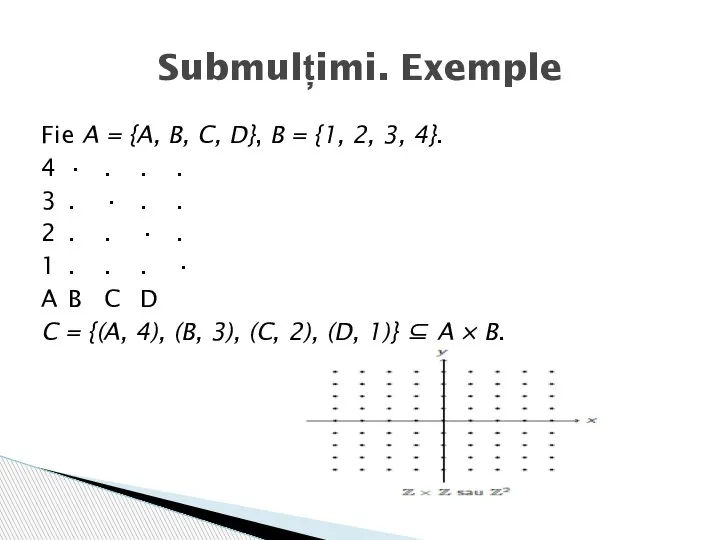
Fie A = {A, B, C, D}, B = {1, 2, 3, 4}.
4 ∙ . . .
3 . ∙ . .
2 . . ∙ .
1 . . . ∙
A B C D
C = {(A, 4), (B, 3), (C, 2), (D, 1)} ⊆ A × B.
Submulțimi. Exemple

O relație binară este o submulțime a unui produs cartezian de forma A × B.
Din acest motiv mai spunem că avem o relație binară de la A la B.
O relație ântre mulț imile A, B și C este o submulțime a A × B × C.
De exemplu,
{(0, 1), (1, 0)} ⊆ Z2;
{(0, 0, 1), (0, 1, 0), (1, 0, 0)} ⊆ Z3.
Relații binare, ternare, n-are

O relație n-ară între mulțimile A1, A2, ..., An este o structură ordonată de forma ρ = (A1, A2, ...,An, R) unde R ⊆ A1 × A2 × ...An. Mulțimea R se numește graficul relației ρ.
În particular, dacă A1 = A2 = ... = An = A spunem că avem o relație n-ară omogenă pe A.
Dacă R = A1 × A2 × ... × An relația se numește universală.
Dacă R = ∅ – relație vidă.
Dacă ρ = (A,B, R) atunci înscierea a ρ b este echivalentă cu (a, b) ∈ R.
De exemplu, fie A = {0, 1, 2} atunci relaț ia “<” este (A, A, {(0, 1), (0, 2)}).
Relații binare, ternare, n-are

Domeniul relației
dom(ρ) = {a ∈ A: ∃ b ∈ B încât (a, b) ∈ R}.
Codomeniul relației
codom(ρ) = {b ∈ B: ∃ a ∈ A încât (a, b) ∈ R}.
Imaginea directă a mulțimii X ⊆ A prin relația ρ este
ρ(X) = {b ∈ B: ∃ a ∈ X, a ρ b}.
Imaginea inversă a mulțimii Y ⊆ B prin relația ρ este
ρ−1(Y) = {a ∈ A: ∃ b ∈ Y , a ρ b}.
Imaginea directă. Imaginea inversă

Fie A = {a, b, c, d} și B = {1, 2, 3, 4}.
Fie R = {(a, 1), (a, 2), (b, 4)} și ρ = (A, B, R).
Atunci ρ({a}) = {1,2}; ρ({a, b}) = {1,2,4}; ρ({c, d}) = ∅;
ρ−1({1}) = {a}; ρ−1({1, 4}) = {a, b}; ρ−1({2}) = ∅.
Fie A = {Student1, Student2, Student3, Student4} și
B = {Curs1, Curs2, ..., Curs∞}.
Fie R = {(Student1, Curs2), (Student2, Curs2), (Student2, Curs4), (Student3, Curs1)} și
ρ = (A,B, R). Utilizați diagrame.
Atunci:
ρ({Student1, Student2}) = {Curs2}; ρ({Student4}) = ∅;
ρ−1({Curs1, Curs2, Curs4}) = {Student1, Student2, Student3}; ρ−1({Curs3}) = ∅.
Imaginea directă. Imaginea inversă

Relația ρ este surjectivă dacă ρ(A) = B.
Relația ρ este totală dacă ρ−1(B) = A.
Relația este injectivă dacă pentru orice a ∈ A este cel mult un element b ∈ B încât (a, b) ∈ R.
Fie o relație binară omogenă ρ = (A, A, R); În acest caz putem folosi expresiile:
“ρ relație binară pe mulțimea A”
“A este înzestrată cu o relație binară“
Relații surjective, injective, binare omogene

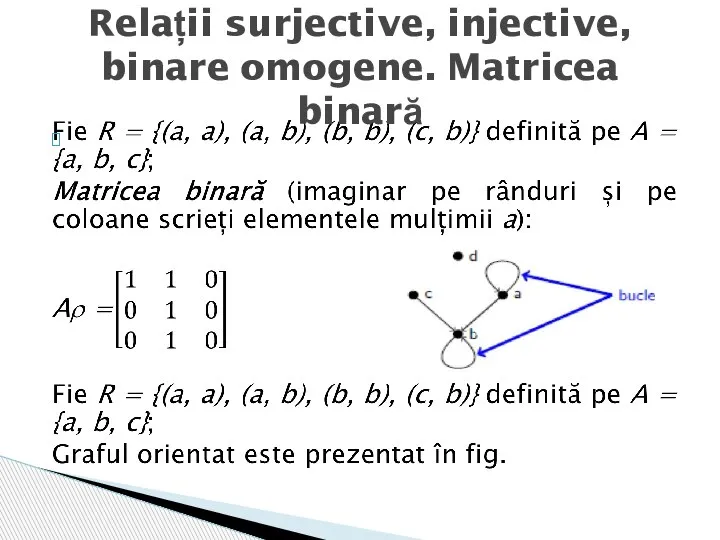
Relații surjective, injective, binare omogene. Matricea binară

Proprietăți: reflexivitate, antireflexivitate

Relația ρ = (A, A, R) se numește simetrică dacă pentru orice (a, b) ∈ R avem (b, a) ∈ R.
De exemplu,
A = {0,1,2,3} și R = {(3, 2), (1, 1), (2, 3), (0, 2), (2, 0)}.
Construiți matricea acestei relații. Construiți matricea transpusă. Matricea relației este simetrică. Construiți graful orientat.
Relația ρ = (A, A, R) se numește asimetrică dacă pentru orice (a, b) ∈ R avem (b, a) ∈ R.
De exemplu,
A = {0, 1, 2, 3} și R = {(3, 2), (2, 3), (0, 2)}.
Relații simetrie, asimetrie

Relația ρ = (A, A, R) se numește antisimetrică dacă pentru orice (a, b) ∈ R avem (b, a) ∈ R cu excepția cazurilor când a = b.
Relația antisimetrică este o relație asimetrică cu cel puțin o pereche de formatul (a, a).
De exemplu,
A = {0, 1, 2, 3} și R = {(3, 2), (1, 1), (0, 2)}.
Relația ρ = (A, A, R) se numește tranzitivă dacă pentru orice (a, b), (b, c) ∈ R avem (a, c) ∈ R.
De exemplu,
A = {0, 1, 2, 3} și R = {(2, 1), (3, 2), (3, 1)}.
Relații antisimetrie, tranzitivitate

Fie relațiile ρ1=(A,A,R1) și ρ2=(A,A,R2), atunci reuniunea:
ρ1∪ρ2 = {(a,b)∈A2:
(a,b)∈R1 sau (a,b)∈R2}. Aρ1⊕Aρ2:aij OR bij
Fie relațiile ρ1=(A,A,R1) și ρ2=(A,A,R2), atunci intersecția:
ρ1 ∩ ρ2 = {(a, b) ∈ A2:
(a, b) ∈ R1 și (a, b) ∈ R2}. Aρ1 ⊗ Aρ2 : aij AND bij.
Fie relațiile ρ1= (A,A,R1) și ρ2=(A,A,R2), atunci compunerea:
ρ1 ∙ ρ2 = {(a, b) ∈ A2: (a, c) ∈ R1 și (c, b) ∈ R2}. Aρ1Aρ2.
Fie relația ρ = (A,A, R) atunci inversarea:
ρ −1 = {(a, b) ∈ A2: (b, a) ∈ R}.
Operații: reuniunea, intersecția, compunerea, inversarea

Fie relația ρ = (A,A,R), dacă ρ nu este reflexivă atunci ea poate fi transformată într-o relație reflexivă adăugând perechi de forma (a, a) unde a ∈ A.
Relația finală se numește închiderea reflexivă a relației ρ.
Închiderea reflexivă este cea mai mică relație reflexivă care conține ρ. “Cea mai mică” în raport cu relația ⊆. Exemplu de închidere reflexivă:
Fie A = {0, 1, 2} și R = {(0, 0), (0, 1), (0, 2), (1, 2)}.
Relația ρ = (A,A, R) nu este reflexivă. Închiderea reflexivă a relației ρ este:
Închiderea reflexivă a relației < este ≤. Închiderea reflexivă a relației ≠ este relația universală.
Închiderea reflexivă

Cea mai mică relație simetrică care conține relația ρ = (A, A, R) se numește închiderea simetrică a lui ρ.
Închiderea simetrică se obține dacă pentru fiecare pereche (a, b) din R adăugăm perechea (b, a).
Închiderea simetrică a relației ρ este ρ ∪ ρ−1.
Fie A = {0, 1, 2} și R = {(0, 0), (0, 1), (0, 2), (1, 2)}. Relația ρ = (A,A, R) nu este simetrică.
Închiderea simetrică a relație ρ este prezentată în fig.
Fie relația ρ = (A, A, R), dacă ρ nu este tranzitivă atunci ρ poate fi transformată într-o relație tranzitivă în felul următor: adăugăm perechea (a, c) dacă ρ conține (a, b) și (b, c). Este un algoritm recursiv.
Închiderea simetrică

Relația finală se numește închiderea tranzitivă a relației ρ.
Exemplu de închidere tranzitivă: Fie A = {0, 1, 2, 3, 4} și R = {(1, 2), (2, 3), (3, 4), (2, 0)}.
Relația ρ = (A,A, R) nu este tranzitivă.
Închiderea tranzitivă a relație ρ este prezentată în fig.
În graful orientat dacă de la un vîrf la altul există un drum atunci aceste vîrfuri trebuie unite printr-un arc în închiderea tranzitivă.
Închiderea tranzitivă

O relație binară omogenă se numește relație de ordine parțială, dacă este reflexivă, antisimetrică și tranzitivă. Exemple:
Relația ≤ pe Z;
Relația ⊆ pe P(Z);
Relația ”a divide b“ pe N.
Pentru relațiile de ordine parțială se foloses simbolurile sau .
O mulțime pe care este definită o relație de ordine parțială se numește mulțime parțial ordonată.
Ordine parțială

Fie (A, ) o mulțime parțial ordonată. Fie a, b ∈ A; dacă a b atunci fie a = b fie a ≠ b.
Dacă a b și a ≠ b, atunci notăm a b și spunem că a este predecesorul lui b;
sau b este succesorul lui a.
Dacă a b și nu există c încît a c b spunem că a este predecesorul imediat (nemijlocit) al lui b.
Exemplu. Fie A = {0, 1, 2}; pe P(A) considerăm relația ⊆. Scrieți predecesorii lui {0, 1, 2}.
Care dintre aceștea sînt predecesori imediați?
Succesor. Predecesor

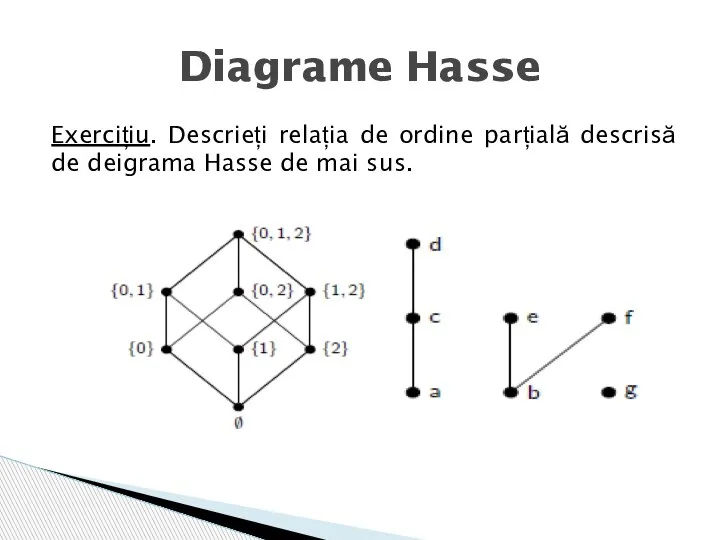
Exercițiu. Descrieți relația de ordine parțială descrisă de deigrama Hasse de mai sus.
Diagrame Hasse

Fie (A, ) o mulțime parțial ordonată. Dacă există a ∈ A cu proprietatea că pentru orice b ∈ A avem a∈ b, atunci a se numește cel mai mic element.
Dacă cel mai mic element există atunci el este unic.
Un element a este minimal dacă nu există b cu b a.
Într-o mulțime parțial ordonată (A, ) două elemente a și b se numesc comparabile dacă a b sau b a.
O relație de ordine parțială în care orice două elemente sînt comparabile se numește relație de ordine totală.
Maxim/minim. Comparabilitate

Fie (A, 1) și (B, 2) două mulțimi parțial ordonate. Putem defini pe A × B următoarea relație de ordine: (a1, b1) (a2, b2) dacă: 1). a1 1 a2 sau 2). a1 = a2 și b1 2 b2.
Această ordine se numește ordine lexicografică.
O relație binară omogenă este relație de echivalență dacă este reflexivă, simetrică și tranzitivă.
Relații de echivalență: “=”. Relații care nu sînt de echivalența: “<”, “≠”.
Ce puteți spune despre matricea binară a relației de echivalență?
Ce puteți spune despre graful orientat a relației de echivalență?
Într-o relație de echivalență ρ = (A, A, R) pentru fiecare element a ∈ A considerăm:
[a]ρ = {b ∈ A: a ρ b}.
Aceste mulțimi nu sînt vide. Aceste mulțimi sînt disjuncte.
Mulțimea de forma [a] ρ se numește clasă de echivalență a elementului a în raport cu relația ρ.
Ordine lexicografică. Relații de echivalență, clase de echivalență

Fie (A, 1) și (B, 2) două mulțimi parțial ordonate. Putem defini pe A × B următoarea relație de ordine: (a1, b1) (a2, b2) dacă: 1). a1 1 a2 sau 2). a1 = a2 și b1 2 b2.
Această ordine se numește ordine lexicografică.
O relație binară omogenă este relație de echivalență dacă este reflexivă, simetrică și tranzitivă.
Ordine lexicografică