Содержание
- 2. Решение алгебраической задачи геометрическим методом. I 1)Построение геометрической модели задачи , т.е. перевод её на язык
- 3. Задача 1.Чтобы ликвидировать опоздание на 1 час , поезд на перегоне в 720км увеличил скорость ,
- 4. S1 = S2, т. .к. S1 + S2 = S3; S1 = x; S2 = 10EF,
- 5. Алгебраический метод Х (км/ч) – скорость поезда по расписанию.
- 6. Теорема Если через произвольную точку Е диагонали АС прямоугольника АВСD проведены прямые FM II AB и
- 8. Скачать презентацию
Слайд 2Решение алгебраической задачи геометрическим методом.
I
1)Построение геометрической модели задачи , т.е. перевод
Решение алгебраической задачи геометрическим методом.
I
1)Построение геометрической модели задачи , т.е. перевод

2)Решение получившейся геометрической задачи;
3)Перевод полученного ответа с геометрического языка на естественный.
II
1)При решении задачи этим методом четко определяется начало действия;
2)Графическая иллюстрация облегчает проведение анализа, составления уравнений, помогает найти несколько способов решения;
3)Расширяется область использования графиков, повышается графическая культура учеников;
4)Совершенствуется техника решения уравнений (разделений переменных);
5)Реализуются внутрипредметные (алгебра и геометрия) и межпредметные (математика и физика) связи.
Слайд 3Задача 1.Чтобы ликвидировать опоздание на 1 час , поезд на перегоне в
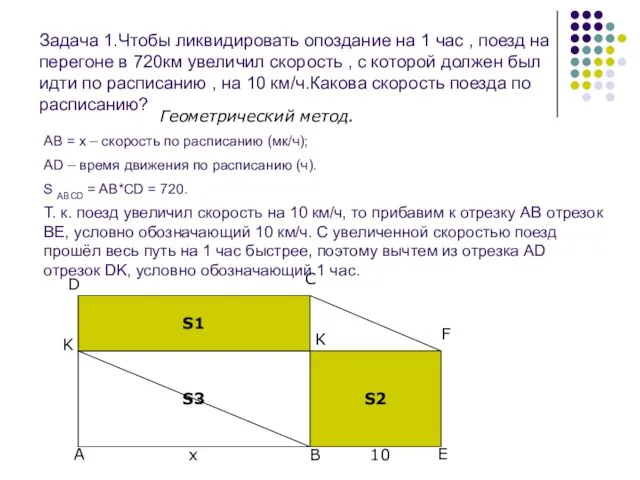
Задача 1.Чтобы ликвидировать опоздание на 1 час , поезд на перегоне в
S3
S2
S1
A
B
E
x
10
K
D
C
F
Геометрический метод.
K
АВ = х – скорость по расписанию (мк/ч);
AD – время движения по расписанию (ч).
S ABCD = AB*CD = 720.
Т. к. поезд увеличил скорость на 10 км/ч, то прибавим к отрезку АВ отрезок ВЕ, условно обозначающий 10 км/ч. С увеличенной скоростью поезд прошёл весь путь на 1 час быстрее, поэтому вычтем из отрезка AD отрезок DK, условно обозначающий 1 час.
Слайд 4S1 = S2, т. .к. S1 + S2 = S3; S1 =
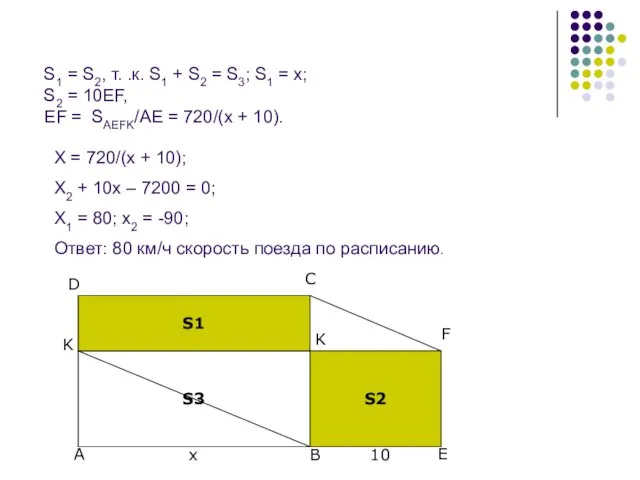
S1 = S2, т. .к. S1 + S2 = S3; S1 =
S3
S2
S1
A
B
E
x
10
K
D
C
F
K
Х = 720/(х + 10);
Х2 + 10х – 7200 = 0;
Х1 = 80; х2 = -90;
Ответ: 80 км/ч скорость поезда по расписанию.
Слайд 5 Алгебраический метод
Х (км/ч) – скорость
поезда
по расписанию.
Алгебраический метод
Х (км/ч) – скорость
поезда
по расписанию.

Слайд 6 Теорема
Если через произвольную точку Е диагонали АС прямоугольника АВСD проведены прямые
Теорема
Если через произвольную точку Е диагонали АС прямоугольника АВСD проведены прямые
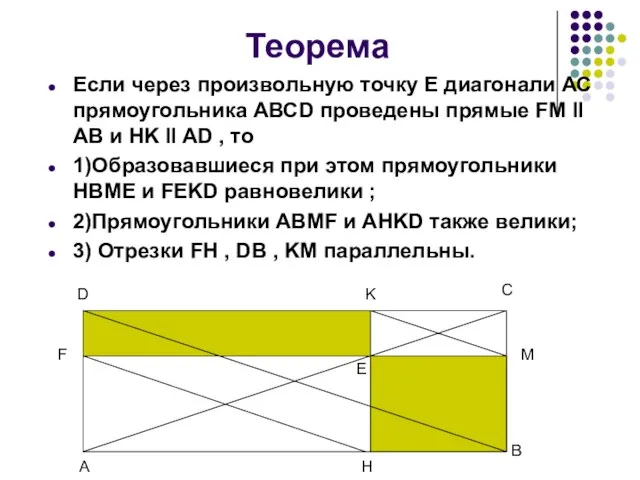
1)Образовавшиеся при этом прямоугольники HBME и FEKD равновелики ;
2)Прямоугольники ABMF и AHKD также велики;
3) Отрезки FH , DB , KM параллельны.
D
K
C
M
B
H
A
F
E
 Советы Бобра Суперзуба
Советы Бобра Суперзуба Презентация на тему Электронный учебник
Презентация на тему Электронный учебник Связь факторов темперамента со способностью к концентрации внимания
Связь факторов темперамента со способностью к концентрации внимания Интернет мощный маркетинговый инструмент в работе салона красоты.
Интернет мощный маркетинговый инструмент в работе салона красоты. Орнамент. Символика в орнаменте
Орнамент. Символика в орнаменте Effective business meetings
Effective business meetings  Страхование от несчастного случая + страхование от заболевания ГЛПС
Страхование от несчастного случая + страхование от заболевания ГЛПС Обработка графической информации
Обработка графической информации Мастер-класс Изготовление и роспись объемных картин из холодного фарфора
Мастер-класс Изготовление и роспись объемных картин из холодного фарфора Презентация на тему Professions
Презентация на тему Professions Йога-ёлка (фотографии)
Йога-ёлка (фотографии) Финансовые отношения в экономике ПОДГОТОВКА К ЕГЭ САФОНОВА Н.С. УЧИТЕЛЬ ИСТОРИИ И ОБЩЕСТВОЗНАНИЯ ЛИЦЕЙ №7 Г. САЯНОГОРСКА
Финансовые отношения в экономике ПОДГОТОВКА К ЕГЭ САФОНОВА Н.С. УЧИТЕЛЬ ИСТОРИИ И ОБЩЕСТВОЗНАНИЯ ЛИЦЕЙ №7 Г. САЯНОГОРСКА Плавания на боку, с элементами захвата утопающего
Плавания на боку, с элементами захвата утопающего Презентация на тему Православные праздники
Презентация на тему Православные праздники  Земля - кормилица
Земля - кормилица История мужской моды и причёсок XVIII — начала XX века
История мужской моды и причёсок XVIII — начала XX века Грибы
Грибы ОСОБЕННОСТИ РЕКЛАМНОГО РЫНКА «МАЛОГО» ГОРОДА
ОСОБЕННОСТИ РЕКЛАМНОГО РЫНКА «МАЛОГО» ГОРОДА Групповые феномены
Групповые феномены Построение третьего вида по двум данным
Построение третьего вида по двум данным Просвещенный абсолютизм Екатерины Великой
Просвещенный абсолютизм Екатерины Великой Презентация на тему Математическая индукция
Презентация на тему Математическая индукция  Новый образовательный стандарт: структура, назначение, функции
Новый образовательный стандарт: структура, назначение, функции Природа и архитектура. Организация архитектурно-ландшафтного пространства
Природа и архитектура. Организация архитектурно-ландшафтного пространства Уголок уединения (проект)
Уголок уединения (проект) Its VISION tea Time! Время чая VISION! Vision Tea Vision Tea – на самый изысканный вкус! Уникальные литовские травяные чаи Традиции и качество Высокотех
Its VISION tea Time! Время чая VISION! Vision Tea Vision Tea – на самый изысканный вкус! Уникальные литовские травяные чаи Традиции и качество Высокотех Interior design
Interior design лекция 4
лекция 4